مقدمه
امروزه جوامع بهشدت به شبکهای پیچیده از زیرساختهای حیاتی بههمپیوسته شامل سیستمهای انرژی، حملونقل، آب و فاضلاب و ارتباطات وابستهاند، بهگونهای که اختلال در یک زیرساخت در اثر وقوع بحران یا ایجاد هرگونه اختلالی در آنها، میتواند به اثرات آبشاری در سایر بخشهای وابسته منجر شود. این پدیده که بهعنوان بحران زیرساختهای حیاتی وابسته به هم شناخته میشود، میتواند به اختلال گسترده در عملکرد روزمره جوامع منجر شود. بهعنوانمثال، ازیکسو، نیروگاهی که از فاضلاب، برق تولید میکند، برای عملکرد خود به شبکه فاضلاب نیاز دارد؛ ازسویدیگر، فاضلاب برای تأمین برق خود به شبکه برق نیاز دارد. مثالی دیگر از وابستگی بین زیرساختهای وابسته به هم این است که زیرساخت فاضلاب بهمنظور تخلیه سیل در زیرساختهای بزرگراهی سیلزده به نیروی الکتریکی نیاز دارد (
سوتچین و همکاران، 2023).
باتوجهبه نقش مهم زیرساختهای حیاتی در تأمین رفاه جوامع، افزایش تابآوری سیستم به مفهوم بهبود توانایی سیستم در برابر اختلالات و تسریع در برابر عملیات بازیابی پس از وقوع یک رویداد مخرب در زیرساختهای حیاتی از اهمیت بسزایی برخوردار است.
بالاکریشنان و همکاران (2020) ، با انجام اقدامات تقویتی در این زیرساختها پیش از وقوع بحران به افزایش تابآوری در زیرساختهای حیاتی پرداختند. باتوجهبه اینکه در شبکههای زیرساختی هریک از اجزای زیرساخت اهمیت خاص خود را دارد، اهمیت هر گره برای شبکهها تا حد زیادی براساس نوع خدمتی که ارائه میدهد و تعداد گرههای زیرساختی که به آن وابسته هستند، متفاوت است (
بالاکریشنان و همکاران (2020).
المغتاوی و همکاران (2021)، یک مدل ریاضی چندهدفه عدد صحیح مبتنی بر بازیابی در جهت افزایش تابآوری زیرساختهای وابسته به یکدیگر آب و برق بعد از وقوع بحران ارائه دادند. آنها با حل این مدل هزینههای کل فرایند بازیابی را کاهش دادند و باتوجهبه محدودیت منابع مالی و زمانی به اولویتبندی گرهها و لینکهایی که باید بازیابی شوند پرداختند. بهمنظور افزایش تابآوری زیرساختهای وابسته به یکدیگر،
رضاپور و شبنم (2024)، روشی نوآورانه مبتنی بر یادگیری تقویتی در جهت بازیابی مشارکتی بین زیرساختهای حیاتی جاده و برق در داکوتای جنوبی که توسط گردباد مختل شده بود ارائه دادند..
ژانک و همکاران (2024)، مدل بهینهسازی دوسطحی برای بازیابی همزمان شبکههای حملونقل و برق پس از وقوع زلزله توسعه دادند.
شاهوردی و همکاران (2024)، مدل ریاضی برای بهینهسازی ترتیب بازسازی زیرساختهای آب و برق و حملونقل بعد از وقوع بحران توسعه دادند و نشان دادند همکاری بین زیرساختها، اولویتبندی و برنامهریزی اقدامات بازیابی موجب تسریع در ارائه خدمات حیاتی بعد از وقوع اختلال در آنها شد.
ژانک و همکاران (2024)، روشی را برای برنامهریزی و تخصیص بهینه منابع تعمیر مانند گروههای تعمیر هنگام رویارویی با بلایای طبیعی و خرابیهای غیرقابلکنترل برای زیرساختهای حملونقل و برق ارائه دادند. باتوجهبه اینکه منابع تعمیرات بعد از وقوع اختلالات برای زیرساختها محدود است،
ژو و همکاران (2019)، مدل تصادفی دومرحلهای در جهت مشخص کردن توالی ترتیب تعمیر سیستمهای زیرساختی حیاتی تحت عدم قطعیت توسعه دادند.
شن و سیقیان (2013)، هر زیرساخت را یک شبکه با گرههای عرضه، انتقال و تقاضا در نظر گرفتند. آنها دو مدل بهینهسازی تحت اختلالات تصادفی در هر کمان را موردمطالعه قرار دادند. مدل اول بر یک شبکه واحد با خرابیهای کوچک تمرکز دارد و به دنبال بازیابی سریع کمانهای شبکه است. در مدل دوم، زیرساختهای وابسته به هم تحت اختلالات بزرگمقیاس باهدف کاهش تلفات و بازگرداندن سریع خدمات با کمترین هزینههای طراحی زیرساختها و عملیات بازیابی در نظر گرفته شده است.
فن و همکاران (2023)، یک مدل یادگیری تقویتی عمیق برای بهینهسازی توالی بازسازی شبکه جادهای بعد از وقوع زلزله یا سیل برای بهبود تابآوری آنها ارائه کردند. بعد از وقوع بحران که به اختلالات در زیرساختها منجر میشود، برخی فعالیتهای بازسازی ممکن است قبل از بازسازی اجزای مهمتر در این زیرساختها انجام شود؛ بنابراین اولویتبندی انجام فعالیتهای بازسازی بهشدت بر زمان بازگرداندن خدمات آنها تأثیرگذار است.
شاهوردی و همکاران (2024)، یک مدل برنامهریزی تصادفی چندمرحلهای با عدم قطعیت برای برنامههای بازرسی و بازسازی زیرساختهای جاده و برق بعد از وقوع بحران توسعه دادند که با مشخص کردن ترتیب عملیات بازیابی به افزایش کارایی و تسریع عملیات بازیابی منجر شدند.
بالاکریشنان و همکاران (2020)، از دو شاخص بحرانی و آسیبپذیری برای رتبهبندی و اولویتبندی گرههای شبکه زیرساختی وابسته به هم استفاده کردند. نمرهای به هر گره اختصاص دادند که نشاندهنده اهمیت و آسیبپذیری آنها در شبکه بود. گرههایی که نمره بالاتری داشتند حیاتیتر بودند و در اولویت بازسازی قرار گرفتند.
اولیوا و همکاران (2014)، با استفاده از روش شاخصهای اهمیت فازی معیارهای فازی را برای ارزیابی اهمیت صنایع سیستمهای زیرساختی وابسته ارائه کردند. آنها با استفاده از شاخصهای اهمیت فازی به اولویتبندی صنایع حیاتی در یک سیستم اقتصادی پرداختند که با اولویتبندی تخصیص منابع، تابآوری کل سیستم اقتصادی را در برابر وقوع اختلالات احتمالی افزایش دادند.
ژائو و همکاران (2018)، با استفاده از روش رتبه صفحه به رتبهبندی زیرساختهای حیاتی پرداختند. آنها از یک مدل شبکهای جهتدار وزندار چندلایه برای نشان دادن وابستگی بین زیرساختهای حیاتی استفاده کردند. آنها با استفاده از این مدل، گرههای بحرانی در شبکههای زیرساختی حیاتی را شناسایی کردند. هر زیرساخت حیاتی بهعنوان یک گره در شبکه نشان داده شد.
کوتلر و همکاران (2020) با استفاده از روش تاپسیس به رتبهبندی گرهها و کمانها در شبکههای زیرساختی برق و مخابرات در شرایط بروز اختلالات چندگانه پرداختند. آنها فرمول بازگشتی برای محاسبه سهم هر مؤلفه در اختلالات چندگانه ارائه دادند.
یوان و همکاران (2017)، با استفاده از تئوری نفوذ نشان دادند که در شبکههای وابسته به هم حداکثر 56/17 درصد از گرهها میتوانند تقویت شوند تا از فروپاشی ناگهانی شبکهها جلوگیری شود.
سوتچین و همکاران (2023)، مدل تصادفی دومرحلهای ارائه دادند که در مرحله اول، تصمیمات تقویت شبکه قبل از بحران و در مرحله دوم، برنامهریزی تعمیرات در فاز بعد از بحران را در نظر گرفتند.
هوانگ و همکاران (2014)، از روشی به نام دانپ که ترکیبی از دو تکنیک دیمتل و ANP است به اولویتبندی زیرساختهای حیاتی پرداختند. مدل دانپ بهطور مؤثری، روابط پیچیده بین زیرساختها را در نظر گرفته و به تعیین اینکه کدام بخش از زیرساختها برای ثبات کلی سیستم، مهمتر هستند، کمک میکند.
ژانک و همکاران (2008)، با استفاده از تحلیل شبکههای اجتماعی زیرساختهای حیاتی را ازنظر مشارکت در وابستگی بین زیرساختها رتبهبندی کردند. آنها نشان دادند که زیرساختهای برق و مخابرات بهدلیل ایجاد نقش مهمشان در ایجاد وابستگی بین زیرساختها از اهمیت ویژهای برخوردارند و آسیبپذیری کل سیستم را افزایش میدهند.
چوپرا و خانا (2015)، شبکه اسکلتی درزمینه تابآوری سیستمهای یکپارچه برق و گاز توسعه دادند. شبکه اسکلتی به مجموعهای از اجزای حیاتی در سیستمهای یکپارچه برق و گاز اشاره دارد که برای حفظ عملکرد کلی سیستم ضروری هستند و این اجزای حیاتیتر در اولویت بالاتری برای تعمیر یا جایگزینی قرارگرفته و موجب افزایش کارایی عملیات بازیابی میشوند و همچنین با اولویتبندی بازیابی اجزای حیاتی، زمان لازم برای بازگرداندن سیستم به عملکرد کامل خود را بهطور قابلتوجهی کاهش میدهند. آنها با تمرکز بر اجزایی که بیشترین تأثیر را بر عملکرد کلی سیستم دارند، تابآوری سیستم را در برابر اختلالات افزایش دادند.
اویانگ و همکاران (2016)، با استفاده از مدلسازی و تحلیل دادهها، مکانهای بحرانی را در زیرساختهای برق و گاز شناسایی کرده و تأثیر اختلالات و وابستگی بین زیرساختها را نیز در این مکانها بررسی کردند.
المغتاوی و همکاران (2023)، یک مدل ریاضی برای بهینهسازی فرایند بازیابی شبکههای زیرساختی وابسته به هم پس از وقوع بحران ارائه دادند. آنها با استفاده از این مدل، کارهای موردنیاز برای بازیابی را اولویتبندی کردند و سپس منابع انسانی موردنیاز برای تعمیر را به این کارها اختصاص دادند و زمانبندی کردند.
وانگ و همکاران (2023)، یک مدل بازی کورنو برای تحلیل امنیت شبکههای زیرساختی در برابر حملات سایبری توسعه دادند. تمرکز این بازی بر بهینهسازی تخصیص منابع دفاعی برای حفاظت از شبکه در برابر حملات با در نظر گرفتن محدودیت منابع و گرههای حیاتی شبکه بود. آنها از روش تاپسیس برای شناسایی گرههای حیاتی استفاده کردند. شناسایی گرههای حیاتی به مدافعان شبکههای زیرساختی حیاتی کمک میکند تا منابع خود را بهطور مؤثرتری تخصیص داده و از شبکه در برابر حملات محافظت کنند.
بارنت و همکاران (2020)، با استفاده از نظریه بازی همکارانه (اثر شاپلی) برای هر گره کلیدی، ائتلافهایی تشکیل دادند و سپس با استفاده از اثر شاپلی برای هر ائتلاف، گرههای غیرکلیدی را در هر ائتلاف اولویتبندی کردند و از نتایج آن در جهت تخصیص بهینه منابع استفاده کردند.
اوگوو و همکاران (2022)، به برنامهریزی عملیات بازیابی سیستمهای زیرساختی وابسته به هم پس از وقوع بلایای طبیعی پرداختند که تمرکز اصلی آنها بر بازیابی امکانات درمانی بود. آنها جهت انجام عملیات بازیابی به اولویتبندی امکانات درمانی مانند بیمارستانها پرداختند که بهشدت به عملکرد صحیح سیستمهای زیرساختی پیچیده وابسته هستند. آنها با اولویتبندی بازیابی این امکانات توانستند به بهبود کارایی و سرعت بازیابی پس از وقوع بلایا کمک کنند.
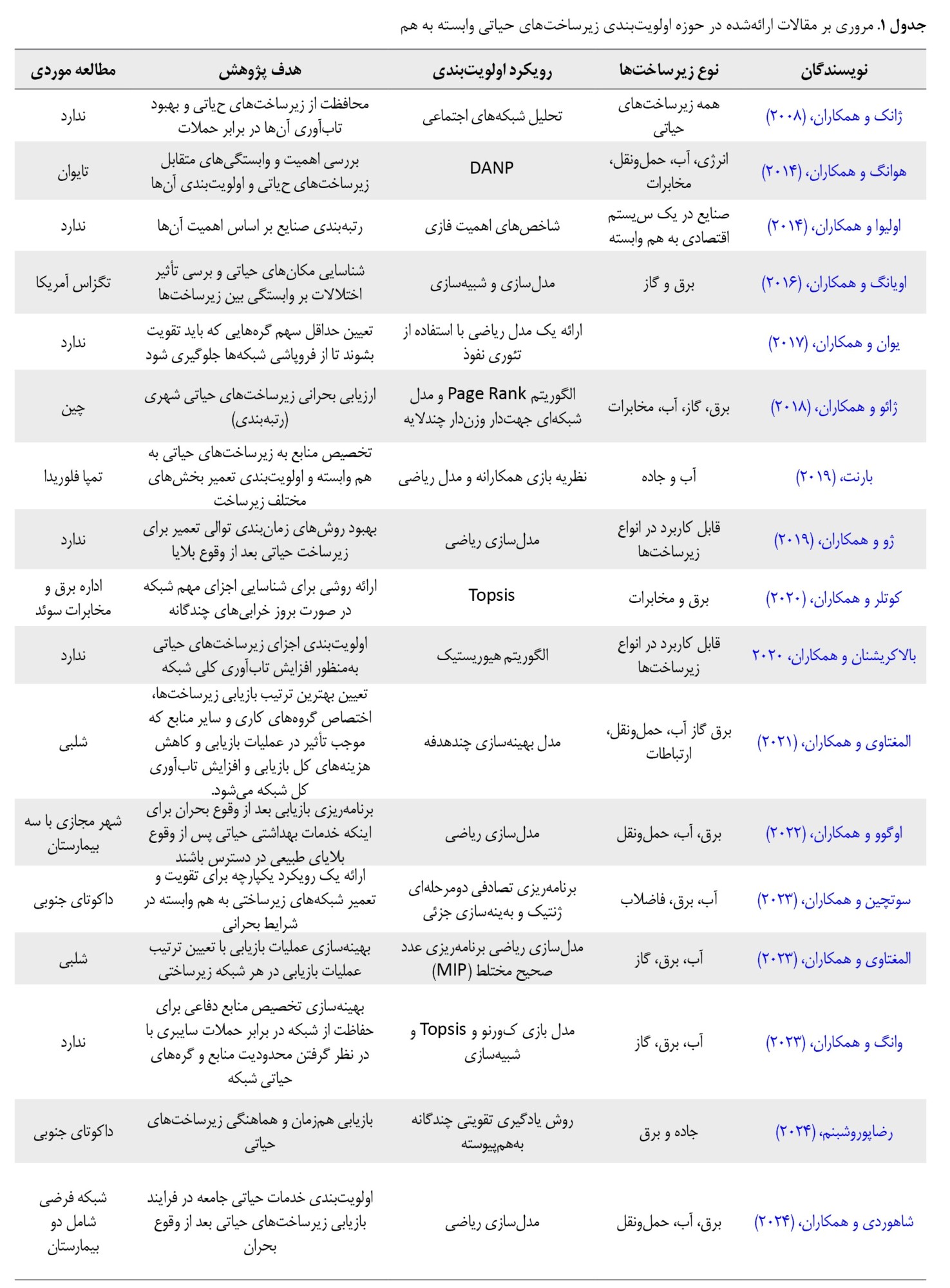
جدول شماره 1 مروری بر مهمترین تحقیقاتی که درگذشته در جهت رتبهبندی زیرساختها بهمنظور افزایش تابآوری زیرساختهای حیاتی وابسته به یکدیگر در فاز قبل یا بعد از بحران انجامشده است، ارائه گردیده است.
باوجود پیشرفتهای قابلتوجه در این حوزه، همچنان چالشهای قابلتوجهی در حل مسئله بازیابی زیرساختهای وابسته به هم وجود دارد. یکی از چالشهای اصلی، عدم وجود رویکردی جامع برای تقویت و بازسازی یکپارچه زیرساختهای آسیبدیده است. همانطور که در
جدول شماره 1 مشاهده میشود، بسیاری از مطالعات صورتگرفته در این زمینه، بر روی فاز پس از بحران تمرکز داشتند و به دنبال روشهایی برای بازیابی سریع زیرساختهای آسیبدیده هستند (
المغتاوی و همکاران، 2023؛
هوانگ و همکاران، 2014؛
ژو و همکاران، 2019؛
شاهوردی و همکاران، 2024).
درحالیکه تحقیقات کمتری در زمینه فاز قبل از بحران و اهمیت تقویت زیرساختها برای افزایش تابآوری آنها انجام شده است. اگرچه مطالعاتی درمورد تقویت زیرساختها در فاز قبل از بحران وجود دارد اما این مطالعات بهطور کامل، وابستگی متقابل بین زیرساختهای حیاتی و محدودیتهای منابع مانند محدودیت در بودجه و نیروی انسانی را در نظر نگرفتند (
سوتچین و همکاران، 2023؛
یوان و همکاران، 2017). درنتیجه روشهای ارائهشده در این مطالعات ممکن است در دنیای واقعی کارآمد نباشند.
بهمنظور پوشش شکاف تحقیقاتی موجود در این زمینه، در این تحقیق بر آنیم تا باتوجهبه محدودیت بودجه، زمان و نیروی کار به اولویتبندی اجزای زیرساختهای حیاتی برای انجام اقدامات تقویتی بهمنظور افزایش تابآوری در آنها میپردازیم. هدف اصلی این پژوهش، ارائه یک روش کارآمد و مبتنی بر داده برای اولویتبندی اجزای زیرساختهای حیاتی بهمنظور انجام اقدامات تقویتی و افزایش تابآوری کل سیستم، باتوجهبه محدودیتهای موجود است. در این پژوهش، تلاش خواهد شد تا با استفاده از روشهای نوین مدلسازی و تحلیل شبکههای پیچیده، روشی جامع برای شناسایی نقاط آسیبپذیر و اولویتبندی اقدامات تقویتی ارائه شود. نوآوری اصلی این پژوهش در تلفیق دو رویکرد زیر نهفته است: اولاً، توجه به وابستگی متقابل زیرساختها و مدلسازی دقیق این وابستگی؛ ثانیاً، استفاده از روشهای نوین تحلیل شبکه برای شناسایی نقاط آسیبپذیر و اهمیت هریک از اجزای شبکه.
در ادامه این مقاله، ابتدا روش پیشنهادی برای اولویتبندی اجزای زیرساختها ارائه شده و نتایج حاصل از کاربرد این روش بر روی یک مطالعه موردی واقعی ارائه خواهد شد. درنهایت، نتیجهگیری و پیشنهادهای پژوهشهای آتی ارائه میشود.
بیان مسئله
جوامع مدرن بر عملکرد مناسب و پایداری شبکههای زیرساختی حیاتی متکی هستند. این زیرساختهای حیاتی را میتوان در چهار گروه حملونقل مثل بزرگراهها، انرژی مثل شبکههای برق، مخابرات مثل شبکه بینالمللی و آب (مثل فاضلاب) طبقهبندی کرد (
لی و همکاران؛ 2007). شبکههای زیرساختی حیاتی برای ارائه خدمات ضروری به جامعه، با یکدیگر تعامل دارند و به یکدیگر وابسته هستند. اگرچه هریک از این زیرساختها براساس عناصر ساختاری خود عمل میکنند، اما در عملکرد، اغلب به یکدیگر وابسته هستند. فعالیتهای انجامشده توسط یک شبکه زیرساخت ممکن است به دریافت سرویس از زیرساخت دیگری نیاز داشته باشد. بهعنوانمثال، یک نیروگاه برق برای عملکرد خود به شبکه آب برای خنکسازی و به شبکه حملونقل برای انتقال سوخت نیاز دارد. وقوع بلایای طبیعی یا انسانی باعث ایجاد اختلال در مقیاس بزرگ در خدمات این زیرساختها میشوند. بازگرداندن خدمات به این زیرساختها پس از وقوع بحران، حیاتی است و ازاینرو، حفظ شبکههای زیرساختی بهصورتی ایمن و تابآور به یکی از چالشبرانگیزترین مسائل برای دولتها در سراسر جهان، بهویژه در چند دهه اخیر تبدیلشده است.
باتوجهبه محدودیتهای زمان، هزینه و سایر منابع لازم است تعیین کنیم که کدام بخشهای شبکه، اولویت بیشتری برای تقویت دارند. هدف این تحقیق، اولویتبندی گرههای حیاتی بهمنظور تقویت این زیرساختها در فاز قبل از بحران با در نظر گرفتن وابستگی بین گرهها در زیرساختهای آب، برق و فاضلاب و باتوجهبه برخی شاخصها نظیر، ظرفیت گره، نوع گره از نوع انتقال یا تأمین و میزان ارتباطات با سایر شبکهها و میزان هزینه تعمیر است، بهگونهای که به شناسایی گرههای حیاتی در شبکه میپردازد و آنها را برای دریافت منابع جهت تقویتشان اولویتبندی میکند. با تقویت گرههای حیاتی، میتوان در زمان بروز بحران، اختلالات را به حداقل رسانده و تابآوری زیرساختها را تا حد امکان افزایش داد.
روش
در این تحقیق از روشهای دیمتل و ارزیابی ریشه برای ارزیابی و اولویتبندی استفاده میشود که در ادامه تشریح میگردد.
روش دیمتل
روش دیمتل یکی از روشهای تصمیمگیری چند معیاره است که برای شناسایی و وزندهی به معیارها در مسائل پیچیده با معیارهای کیفی و کمی متعدد به کار میرود. این روش توسط گابوس و فونتلا در سال 1972 توسعه یافته است. در استفاده از این روش بهترتیب از دو منبع (
ژانگ و همکاران، 2019)،
یزدانی و همکاران، 2017) استفاده شده است که مقاله
یزدانی و همکاران (2017)، برای مراحل کلی این روش و منبع دوم
ژانگ و همکاران (2019) برای تعیین وزن معیارها استفادهشده است. مراحل اصلی روش دیمتل به شرح زیر است (
یزدانی و همکاران، 2017):
گام اول: شناسایی معیارها
اولین قدم در روش دیمتل، شناسایی تمام معیارهای مرتبط با مسئله موردنظر است. این معیارها میتوانند کیفی یا کمی باشند.
گام دوم: ایجاد ماتریس ارتباط مستقیم (M)
در این مرحله، از خبرگان یا تصمیمگیرندگان یا افرادی که نسبت به ماهیت مسئله، شناخت کافی و لازم را دارند خواسته میشود تا روابط متقابل بین هر دو معیار را بهصورت عددی نشان دهند. برای این منظور، از یک طیف مقایسهای مانند (0) تا (4) استفاده میشود. هر عدد در این طیف، نشاندهنده شدت تأثیر یک معیار بر معیار دیگر است: بدون تأثیر (0)، تأثیر کم (1)، تأثیر متوسط (2)، تأثیر زیاد (3) و تأثیر بسیار زیاد (4). با این کار، یک ماتریس رابطه مستقیم (M) با ابعاد n×n به دست میآید که در این ماتریس، هر عنصر (aij) نشاندهنده میزان تأثیر معیار i بر معیار j و n تعداد معیارها را مشخص میکند (فرمول شماره 1).
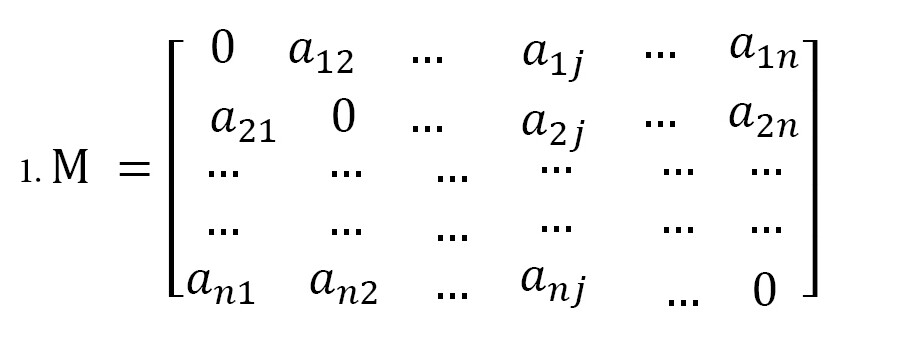 گام سوم: بیمقیاسسازی ماتریس ارتباط مستقیم (M)
گام سوم: بیمقیاسسازی ماتریس ارتباط مستقیم (M)
پس از ایجاد ماتریس رابطه مستقیم (M)، ماتریس نرمال (N) با استفاده از فرمولهای شماره 2 و 3 به دست میآید. هر عنصر در ماتریس N در بازه 0 تا 1 قرار دارد.
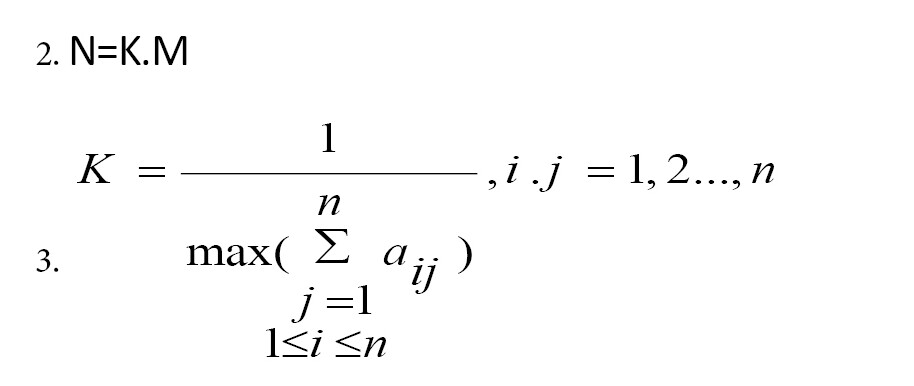 گام چهارم: محاسبه ماتریس رابطه کلی (T)
گام چهارم: محاسبه ماتریس رابطه کلی (T)
ماتریس رابطه کلی (T) با استفاده از فرمول شماره 4 به دست میآید که در آن (I) ماتریس واحد است. هر عنصر tij در این ماتریس نشاندهنده تأثیرات غیرمستقیمی است که معیار i بر معیار j دارد و ماتریس T روابط کلی بین هر جفت از متغیرهای تصمیم را نشان میدهد.
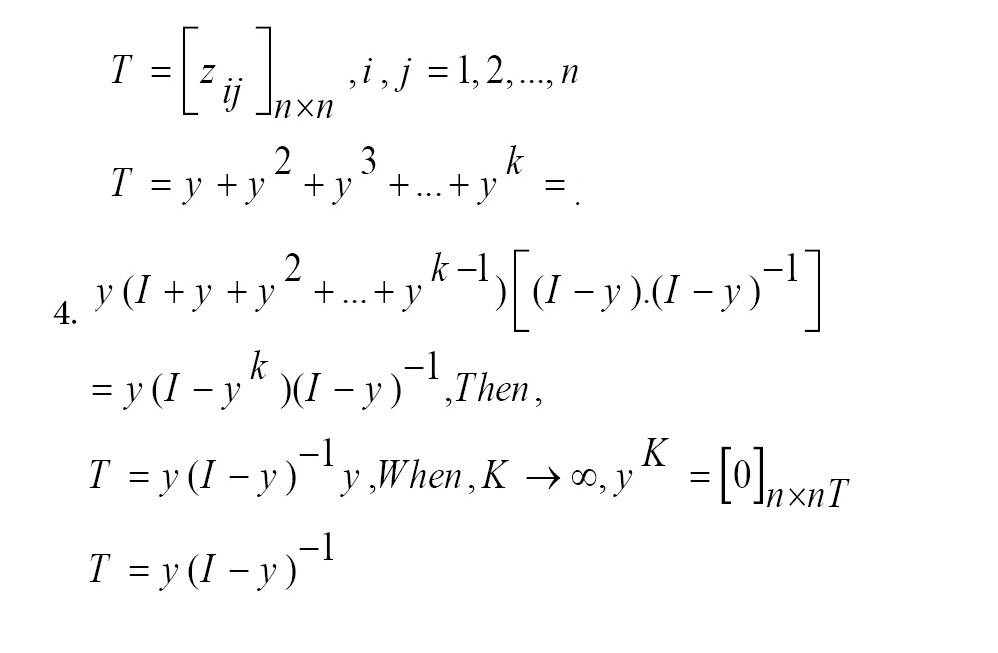 گام پنجم
گام پنجم
در ماتریس روابط کل که با T نمایش داده میشود، مجموع سطرها و مجموع ستونها به ترتیب با بردارهای D و R نشان داده میشوند. این بردارها با استفاده از فرمولهای شماره 5 و 6 بهدستآمدهاند.
 گام ششم: تعیین مقدار آستانه (A)
گام ششم: تعیین مقدار آستانه (A)
ازآنجاییکه ماتریس T چگونگی تأثیر یک عامل بر عامل دیگر را نشان میدهد، تعیین یک مقدار آستانه (A) برای تصمیمگیرنده ضروری است. این مقدار به شفافسازی روابط ساختاری بین معیارها کمک میکند و درعینحال پیچیدگی کل سیستم را در سطح قابلقبولی نگه میدارد. تعیین مقدار آستانه معمولاً توسط کارشناسان و باهدف تعیین حداقل سطح تأثیرگذاری انجام میشود. اگر مقدار همبستگی بین دو عنصر در ماتریس T کمتر از A باشد، رابطه تأثیرگذاری بین آنها از نقشه حذف میشود. تنها تأثیراتی که از مقدار A بزرگتر هستند، انتخاب و در نمودار جهتدار نشان داده میشوند. در این مقاله، مقدار A با محاسبه میانگین عناصر ماتریس T، طبق فرمول شماره 7 محاسبه میشود. در این فرمول، N تعداد کل عناصر ماتریس T است.
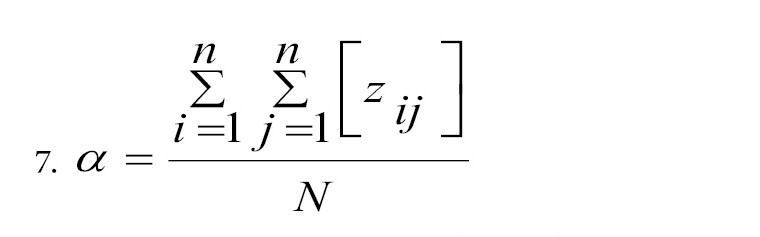 گام هفتم: توسعه دیاگرام علی
گام هفتم: توسعه دیاگرام علی
دیاگرام علی، روشی برای طبقهبندی درجه اهمیت هر معیار است. این دیاگرام نشان میدهد که یک معیار بهراحتی بهعنوان معیار اثرپذیر یا معیار اثرگذار طبقهبندی میشود. براساس این دیاگرام، اهمیت هر معیار را میتوان شناخت و میتوان معیارهای علتومعلول را شناسایی و گروهبندی کرد. بهطور خاص، (Dk -Rk) و (Dk+Rk) بهترتیب برجستگی و ارتباط نامیده میشوند. برجستگی نشاندهنده درجه اهمیت یک معیاراست. رابطه را میتوان بهعنوان شاخصی برای قضاوت در مورد اینکه آیا یک معیار عامل علت است یا عامل معلول در نظر گرفت. اگر مقدار (Dk+Rk) مربوط به یک معیار، مثبت باشد، در گروه علت قرار میگیرد و اگر مقدار آن منفی باشد، یک معیار معلولی است.
گام هشتم: محاسبه وزن معیارها
با استفاده از فرمول شماره 8 وزن هر معیار قابلمحاسبه است (
بایکاس اوغلو وگلچوک، 2017).
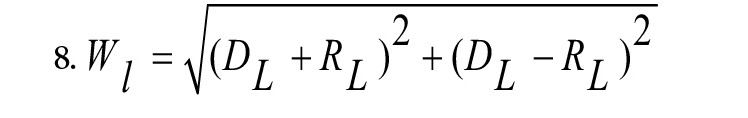
درنهایت، وزن نرمالشده هر معیار مطابق فرمول شماره 9 محاسبه میشود.
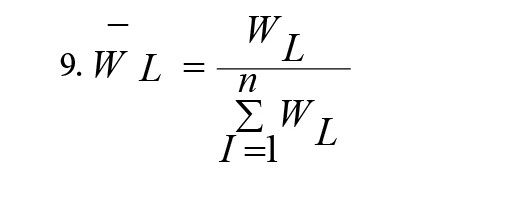
وزن نهایی زیرمعیارها را میتوان با استفاده از فرمول شماره 10 محاسبه کرد.
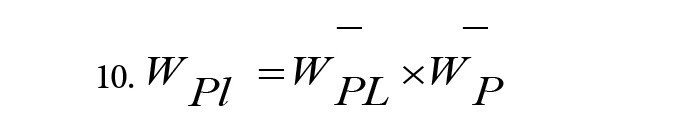
که وزن معیارهای اصلی و وزن محلی زیرمعیارها است. Wp1 وزن کل است. وزن معیارهای اصلی و زیرمعیارها نیز با استفاده از مراحل بالا محاسبه میشود.
روش ارزیابی ریشه
در این پژوهش، از روش ارزیابی ریشه بهعنوان یک روش نوآورانه در تصمیمگیری چند معیاره برای اولویتبندی گرهها در زیرساختهای حیاتی قبل از وقوع بحران استفاده میکنیم. این روش در سال 2023 توسط ستوده اهوری ارائه شده است و بهدلیل ویژگیهای منحصربهفردی همچون ماهیت جبرانکننده جدید، قابلیت جبران جزئی و استفاده از تابع تجمیع ریشهای، به ابزاری مناسب برای اولویتبندی گرهها در زیرساختهای حیاتی تبدیلشده است و به ما این امکان را میدهد عوامل مختلفی را که بر عملکرد یک گره در طول یک بحران تأثیر میگذارند را در نظر بگیریم (
ستوده اهوری، 2023).
یک مسئله تصمیمگیری شامل مجموعهای متناهی از m گزینهAi,i=1,…,m در نظر بگیرید که لازم است نسبت به مجموعهای از n معیار cj,j=1,…,n رتبهبندی شوند. معیارها به دو دسته سودمند و غیرسودمند تقسیم میشوند. اگر aij را بهعنوان عملکرد گزینه i در معیار تصمیم j در نظر بگیریم، ماتریس تصمیم برای m گزینه و n معیار فرمول شماره 11 خواهد بود.
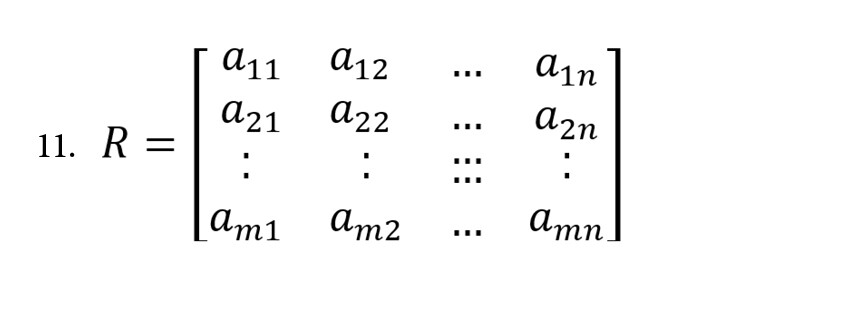
وزن اختصاص دادهشده به معیار jام با wj>0 با نشان داده میشود بهگونهای که برقرار میباشد. بدیهی است که فرآیند تعیین وزن معیارها خارج از محدوده این روش قرار میگیرد. حال به شرح مراحل روش RAM که برای رتبهبندی گزینههای موجود استفاده میشود، میپردازیم. روش ارزیابی ریشه از مراحل زیر تشکیلشده است (
ستوده اهوری، 2023):
گام اول
نرمالسازی ماتریس تصمیمگیری با فرمول نرمالسازی مجموع خطی را با استفاده از فرمول شماره 12 داریم:
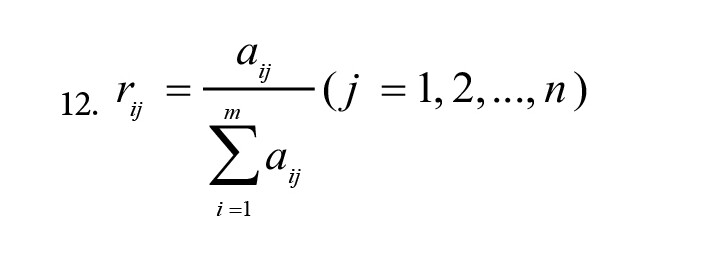 گام دوم
گام دوم
محاسبه ماتریس تصمیمگیری نرمالشده موزون را با استفاده از فرمول شماره 13 داریم:
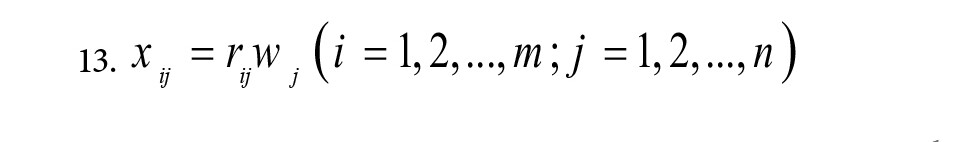 گام سوم
گام سوم
محاسبه مجموع امتیازهای نرمالشده با وزندهی معیارهای سودمند و غیرسودمند برای گزینه iام را با استفاده از فرمولهای 14 و 15 داریم:
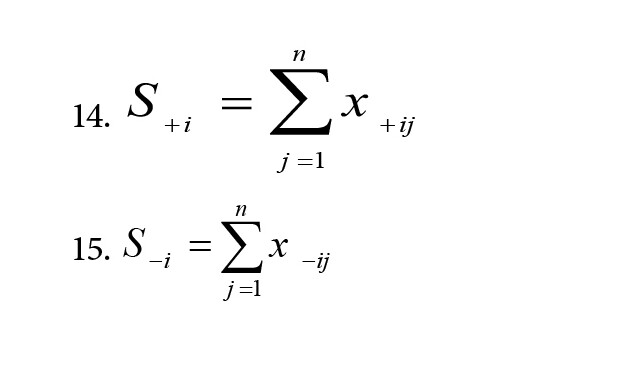 گام چهارم
گام چهارم
محاسبه امتیاز کلی هر گزینه با استفاده از تابع تجمیع. در مرحله چهارم، روش RAM از یک تابع تجمیع برای محاسبه امتیاز نهایی (کل) هر گزینه (Ai) استفاده میکند. این تابع تجمیع، تأثیر جداگانه معیارهای سودمند (S
+i) و غیرسودمند (S
-i) را که در مرحله قبل با استفاده از فرمولهای 14 و 15 محاسبهشدهاند، در نظر میگیرد. تابع تجمیع بهصورت فرمول شماره 16 تعریف میشود:
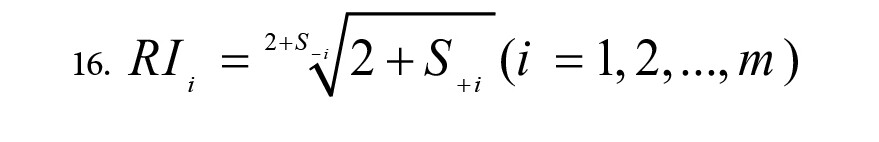 گام پنجم
گام پنجم
رتبهبندی گزینهها با استفاده از مقدار RI1.
یافته ها و بحث
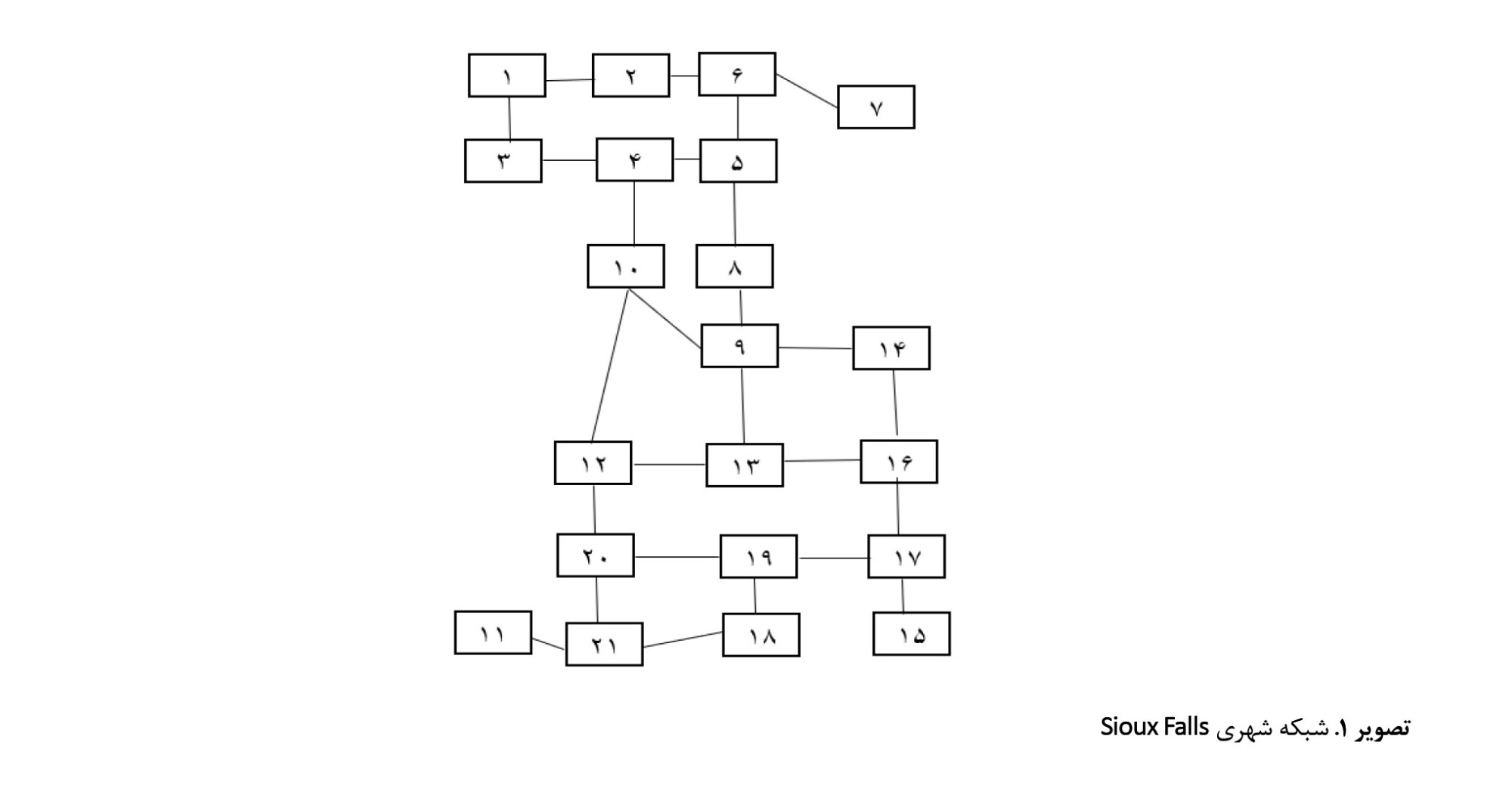
شبکه های زیرساختی شهری، مانند شبکههای برق، آب و فاضلاب، برای عملکرد روان جوامع مدرن ضروری هستند. خرابی در این شبکهها میتواند به اختلالات گسترده، از دست دادن خدمات حیاتی و حتی تلفات جانی منجر شود. بهدلیل محدودیت منابع برای تقویت و ارتقای زیرساختها در دنیای واقعی، شناسایی و اولویتبندی گرههای حیاتی در این شبکهها برای اطمینان از تابآوری و عملکرد آنها در برابر اختلالات احتمالی از اهمیت بالایی برخوردار است. بهمنظور بررسی عملکرد الگوریتمهای تشریحشده، از شبکه شهری سیوکس فالز در داکوتای جنوبی استفاده میکنیم که در تحقیقات گذشته برای مسائل ترافیک مورداستفاده قرارگرفته است. ما این دادهها را از دادههای مقاله
سوتچین و همکاران (2023) استخراج میکنیم که دادههای مورداستفاده در این تحقیق، یک شبکه وابسته از زیر ساختهای آب و برق و فاضلاب میباشد که شامل 24 گره است که در این تحقیق ما از 24 گره که از انواع، گرههای عرضه، انتقال و تقاضا بودند، از 21 گره آن که فقط شامل گرههای انتقال و عرضه هستند استفاده میکنیم و از گرههایی که صرفاً فقط از نوع تقاضا هستند بهعلت اینکه نمیتوانیم آنها را جز گرههای با اهمیت در عملکرد شبکه در نظر بگیریم صرفنظر شده است (3 گره حذف شدند).
همانطور که در
تصویر شماره 1، قابلمشاهده است، این شبکه شامل 21 گره و 23 کمان است.
بودجه تقویت هر زیرساخت معادل ۵ درصد از کل هزینه تقویت تمام کمانهای آن زیرساخت در نظر گرفتهشده است. فرض میکنیم گرههای تقاضا دارای درجه اهمیت یکسان بوده و اهمیت سیستم برق، دو برابر اهمیت سیستم فاضلاب و آب در نظر گرفته شده است. علاوهبراین در این تحقیق در قسمتهایی که نیاز بوده است از نظر خبرگان بهرهگیری شود، منظور از خبرگان افرادی هستند که شناخت کافی و لازمی نسبت به شبکههای زیر ساختی آب، برق و فاضلاب شهری دارند.
جدول شماره 2، خلاصهای از پارامترهای مسئله مربوط به زیرساختهای برق، آب و فاضلاب را نشان میدهد. پارامترها شامل گرههای تقاضا، گرههای تأمین، گرههای انتقال و پارامترهای تقاضا، عرضه، ظرفیت کمان، ظرفیت گره، زمان تعمیر و هزینه تقویتی است.
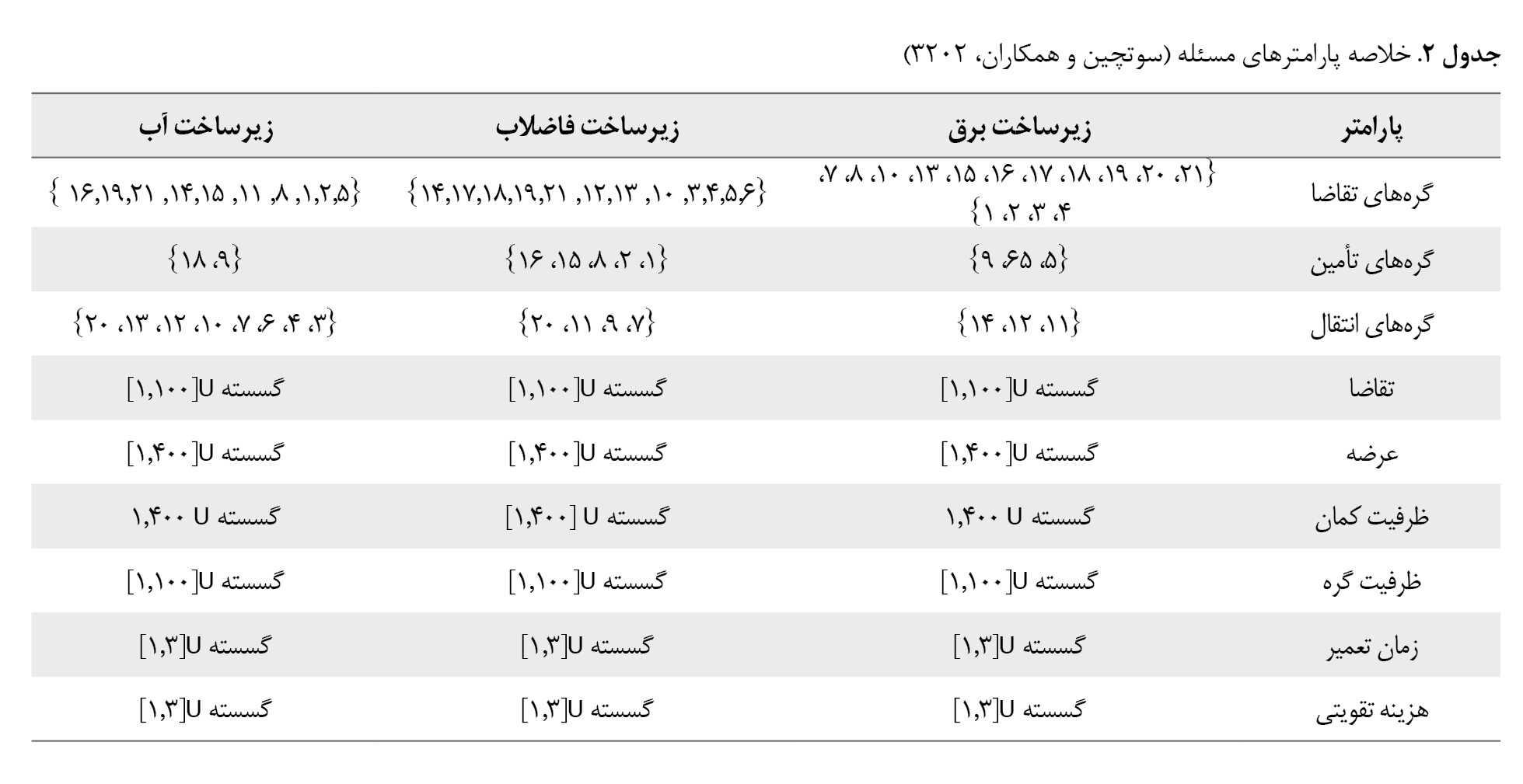
گرههای تقاضا گرههایی هستند که به برق، آب یا فاضلاب نیاز دارند. گرههای تأمین، گرههایی هستند که جهت تأمین برق، آب یا فاضلاب مورداستفاده قرار میگیرند. گرههای انتقال گرههایی هستند که برق، آب یا فاضلاب را از یک گره به گره دیگر منتقل میکنند. پارامتر تقاضا مقدار برق، آب یا فاضلاب موردنیاز در هر گره تقاضا و پارامتر عرضه، مقدار برق، آب یا فاضلاب موجود در هر گره تأمین است. ظرفیت کمان، حداکثر مقدار برق، آب یا فاضلابی است که میتواند از طریق هر کمان جریان یابد و ظرفیت گره، حداکثر مقدار برق، آب یا فاضلابی است که میتواند در هر گره ذخیره شود. پارامتر زمان تعمیر، زمانی است که طول میکشد تا یک گره یا کمان معیوب، تعمیر شود. پارامتر هزینه تقویتی نیز هزینه تقویت گره است.
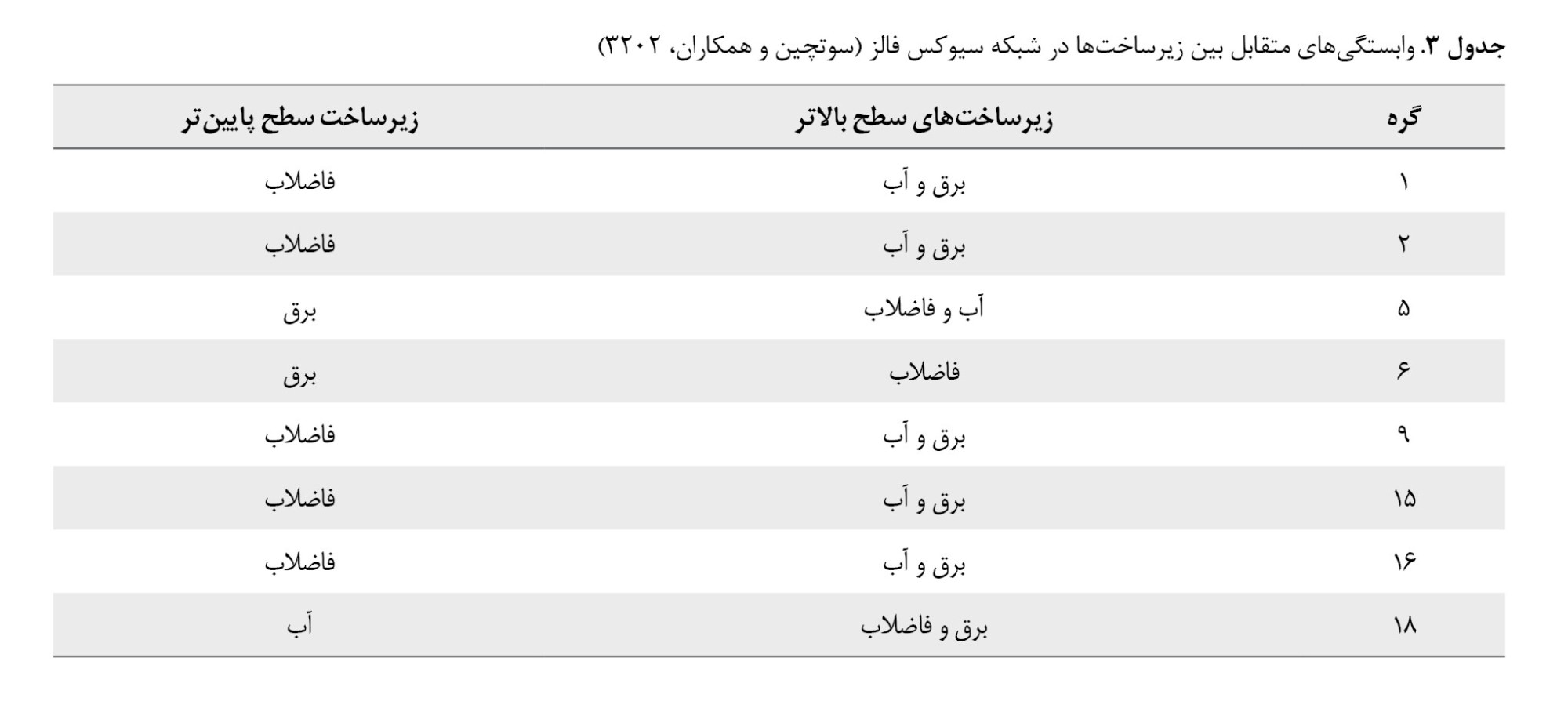
جدول شماره 3 وابستگیهای متقابل بین زیرساختهای مختلف در شبکه شهری سیوکس فالز را نشان میدهد. ستون دوم این جدول نشان میدهد که چه خدماتی توسط یک گره وابسته مورد نیاز است. ستون سوم آن نشان میدهد که چه خدماتی توسط یک گره تأمینکننده ارائه میشود. بهعبارتدیگر، نشان میدهد که هر گره برای کارکرد صحیح به چه منابعی از سایر گرهها نیاز دارد و در مقابل چه منبعی را برای شبکه تأمین میکند. بهعنوانمثال، برق و فاضلاب در ستون دوم مربوط به گره 18، به این معنی است که گره 18 یک تصفیهخانه آب است که برای عملکرد به برق و فاضلاب نیاز دارد. آب در ستون سوم مربوط به گره 18، به این معناست که خروجی گره 18، آب تصفیهشده است. فاضلاب در ستون دوم مربوط به گره 6، به این معنی است که گره 6 یک نیروگاه است که برای تولید برق به فاضلاب نیاز دارد.
بنابراین،
جدول شماره 3 به ما کمک میکند تا روابط و وابستگیهای مهم بین اجزای مختلف شبکه زیرساخت شهری را درک کنیم. اختلال در یک گره (مثلاً کمبود فاضلاب برای نیروگاه) میتواند بر عملکرد سایر گرهها (مثلاً کمبود برق برای تصفیهخانه آب) و درنهایت بر کل شبکه تأثیر بگذارد. اختلال در تأمین خدمات از گرههای بالادست میتواند اثرات آبشاری داشته باشد و بر گرههای پاییندست که به آن خدمات وابسته هستند، تأثیر بگذارد.
 تعیین وزن معیارها و زیرمعیارها
تعیین وزن معیارها و زیرمعیارها
در این شبکه، 21 گره، گزینههای ما هستند و پنج معیار اصلی ظرفیت گره (C_1) گره تأمین (C
2)، گره انتقال (C
3)، ارتباط با سایر شبکهها مثل ارتباطات (C
4) و معیار هزینه تعمیر (C
5) و سه زیرمعیار از نوع زیرساخت برق (C
i1)، آب (C
i2) و فاضلاب (C
i3) موجود است که i شماره معیار اصلی است که زیرمعیارها به آن تعلق دارند.
ابتدا برای هر زیرمعیار، برایناساس که زیرساخت برق، اهمیتی دو برابر زیرساختهای آب و فاضلاب دارد، وزن محلی تعیین میکنیم. در این حالت، وزن زیرمعیار برق، 0/5 و وزن محلی زیرمعیارها دیگر را 0/25 در نظر گرفتیم. جهت استفاده از روش ارزیابی ریشه بهمنظور اولویتبندی گرهها باید وزن معیارها را داشته باشیم. در این زیر بخش ابتدا با استفاده از روش دیمتل به تشریح جزئیات مربوط به مراحل تعیین وزن معیارهای اصلی پرداخته و سپس به نحوه محاسبه وزن محلی هر زیرمعیار و وزن نهایی آن تحت معیارهای اصلی مربوطه میپردازیم.
ابتدا برای هر زیرمعیار، برایناساس که زیرساخت برق، اهمیتی دو برابر زیرساختهای آب و فاضلاب دارد، وزن محلی تعیین میکنیم. در این حالت، وزن زیرمعیار برق، 0/5 و وزن محلی زیرمعیارها دیگر را 0/25 در نظر گرفتیم. جهت استفاده از روش ارزیابی ریشه بهمنظور اولویتبندی گرهها باید وزن معیارها را داشته باشیم. در این زیربخش ابتدا با استفاده از روش دیمتل به تشریح جزئیات مربوط به مراحل تعیین وزن معیارهای اصلی پرداخته و سپس به نحوه محاسبه وزن محلی هر زیرمعیار و وزن نهایی آن تحت معیارهای اصلی مربوطه میپردازیم.
تعیین وزن معیارهای اصلی
ماتریس روابط مستقیم اولیه (M) در
جدول شماره 4 نشان دادهشده است. ماتریس M یک ماتریس 5 در 5 است که با مقایسههای جفتی ازنظر تأثیرات و جهتها بین معیارها بهدستآمده است.
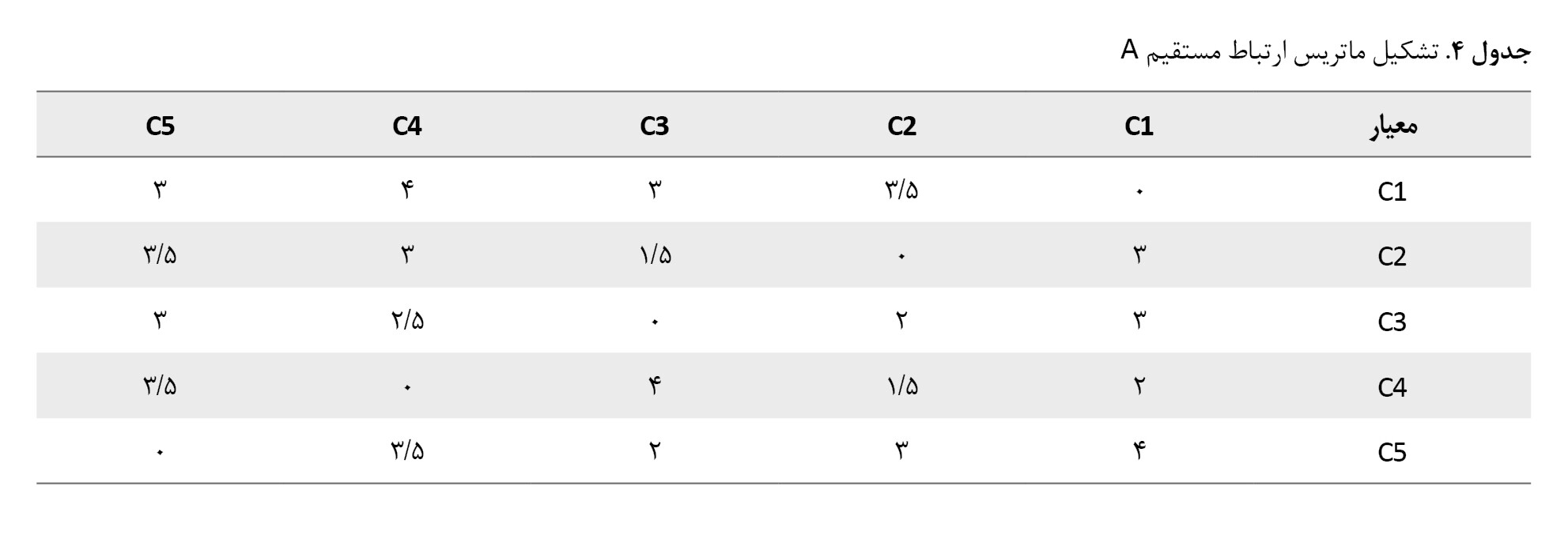
از ماتریس M در
جدول شماره 4، ماتریس روابط مستقیم نرمال (N) به دست میآید که در
جدول شماره 5 نشان داده شده است.
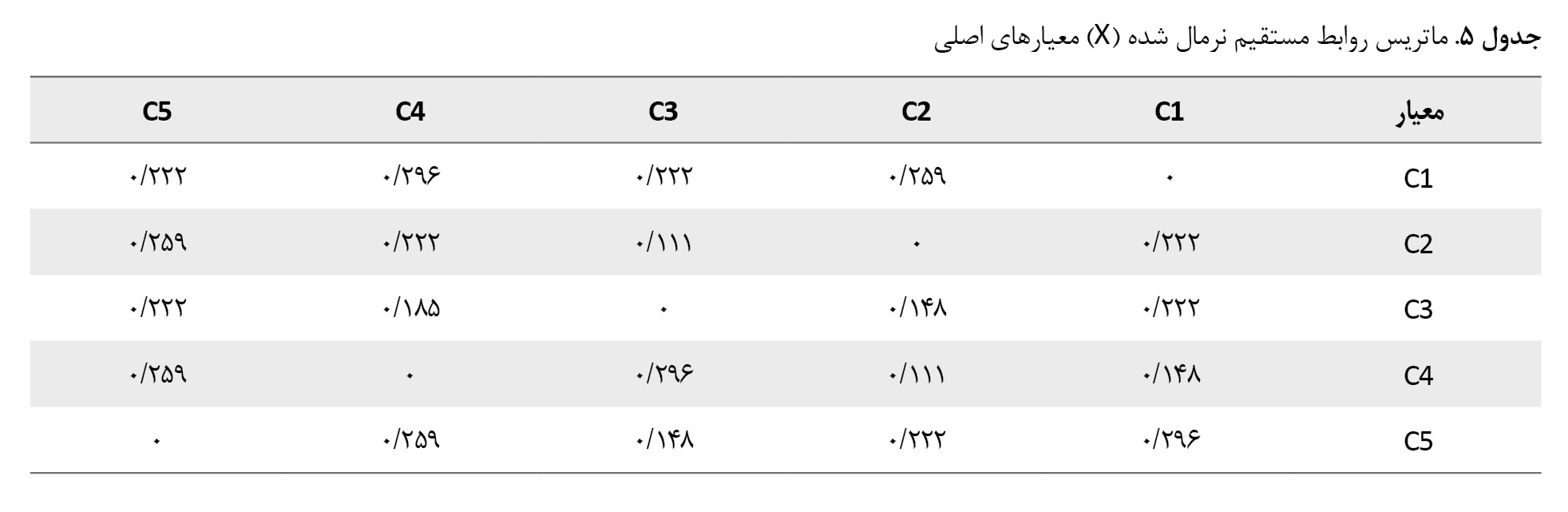
سپس، ماتریس تأثیرات کل (T)، در
جدول شماره 6 نشان داده میشود.
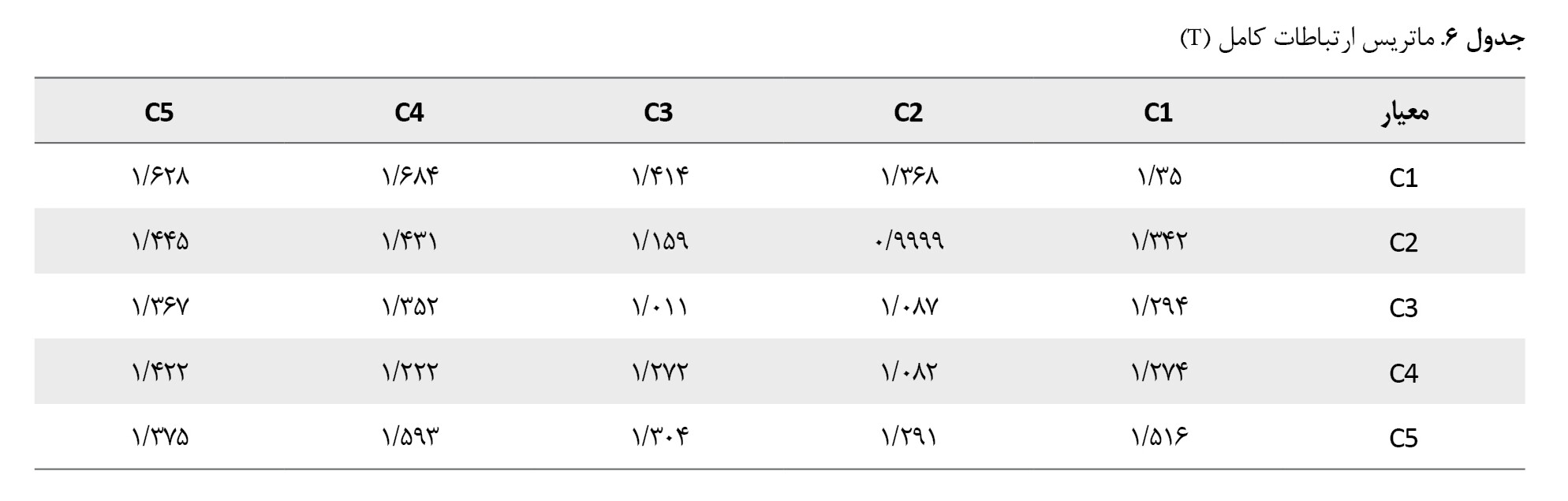
حال، مجموع سطرها و ستونها که بهترتیب با بردارهای d و r نشان داده میشوند، محاسبه شده و در
جدول شماره 7 نشان داده شده است.
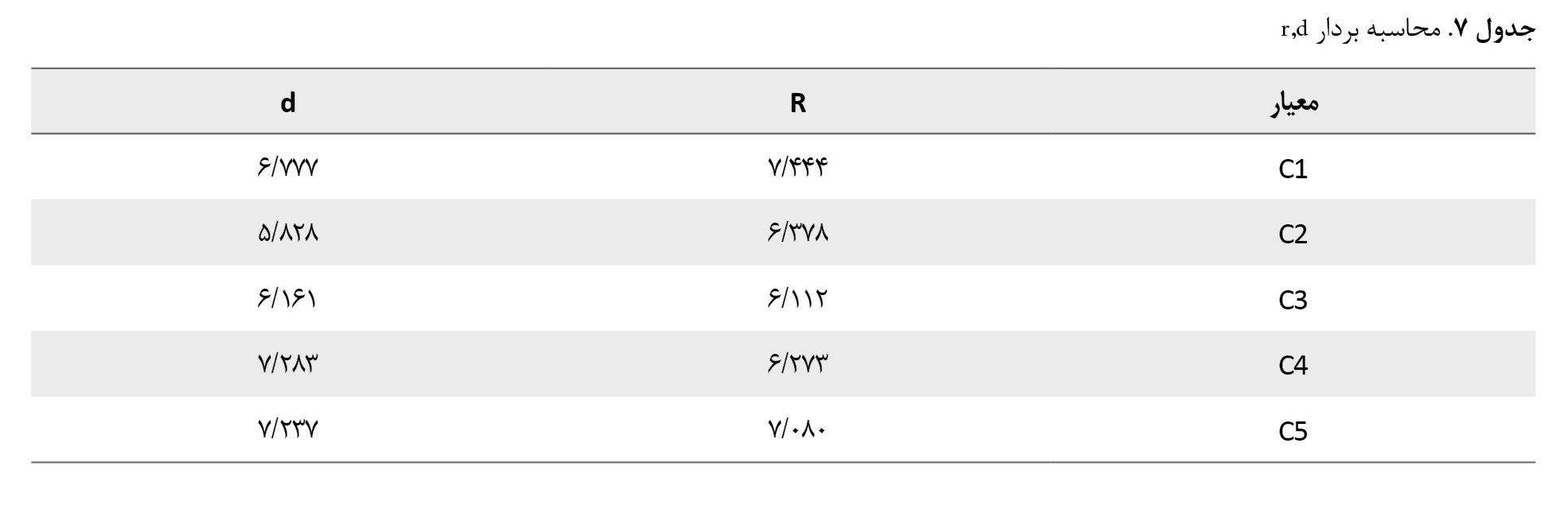
نمودار علتومعلول، همانطور که در
تصویر شماره 2 نمایش داده شده، با ترسیم دادههای
جدول شماره 7 به دست میآید.

براساس مقادیر بهدستآمده در
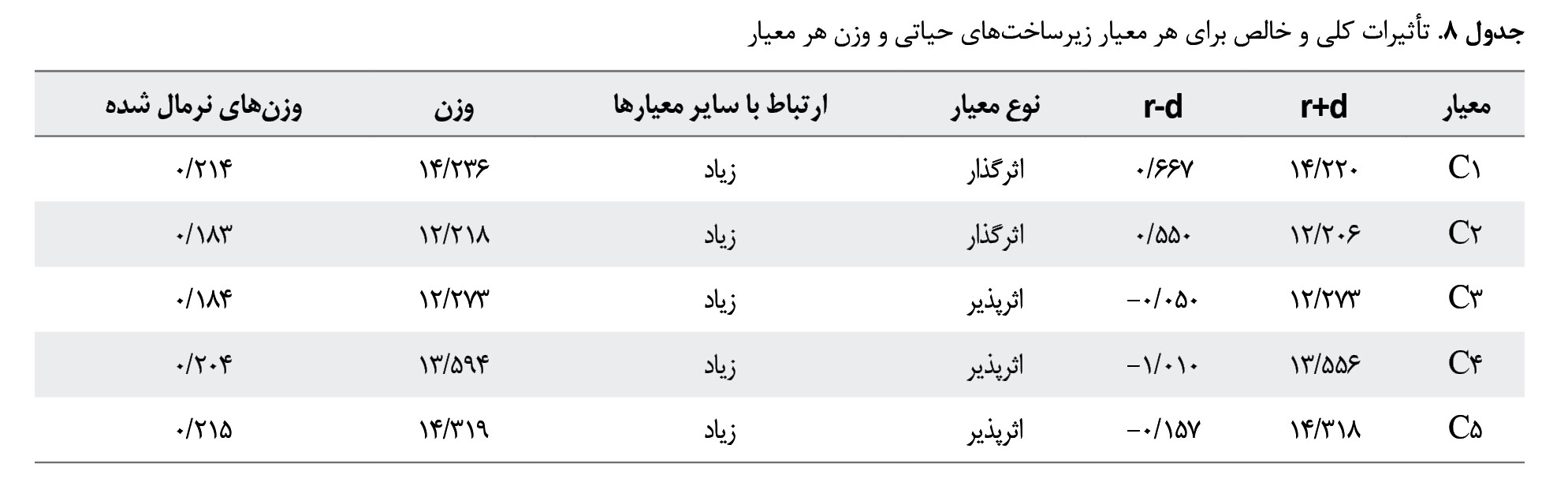
جدول شماره 7، مجموعه دادههای (d+r) و (d-r) با استفاده از فرمولهای 5 و 6 محاسبه میشوند. پسازآن، وزن نرمال شده هر گزینه تصمیمگیری با استفاده از فرمولهای 8 و 9 به دست میآید. نتایج این محاسبات در
جدول شماره 8 نشان داده شده است.
نمودار علیتی که در
تصویر شماره 2 نشان دادهشده است، با رسم دادههای
جدول شماره 8 بهدستآمده است. مقادیر (r-d) محور عمودی نمودار است که میزان تأثیرگذاری هر معیار را نشان میدهد و هرچه مقدار آن بیشتر باشد به این معنی است که آن معیار با سایر معیارها، تعامل بیشتری دارد و اهمیت آن معیار بیشتر است. همانطور که در
جدول شماره 8 مشاهده میشود، معیار ظرفیت گره (C
1) بیشترین اهمیت را دارد. محور افقی نمودار
تصویر شماره 2 بیانگر مقادیر (r+d) میباشد که میزان تأثیرپذیری آن معیار را نشان میدهد. در
جدول شماره 8 معیار هزینه تعمیر (C
2) تأثیرپذیرترین معیار است.
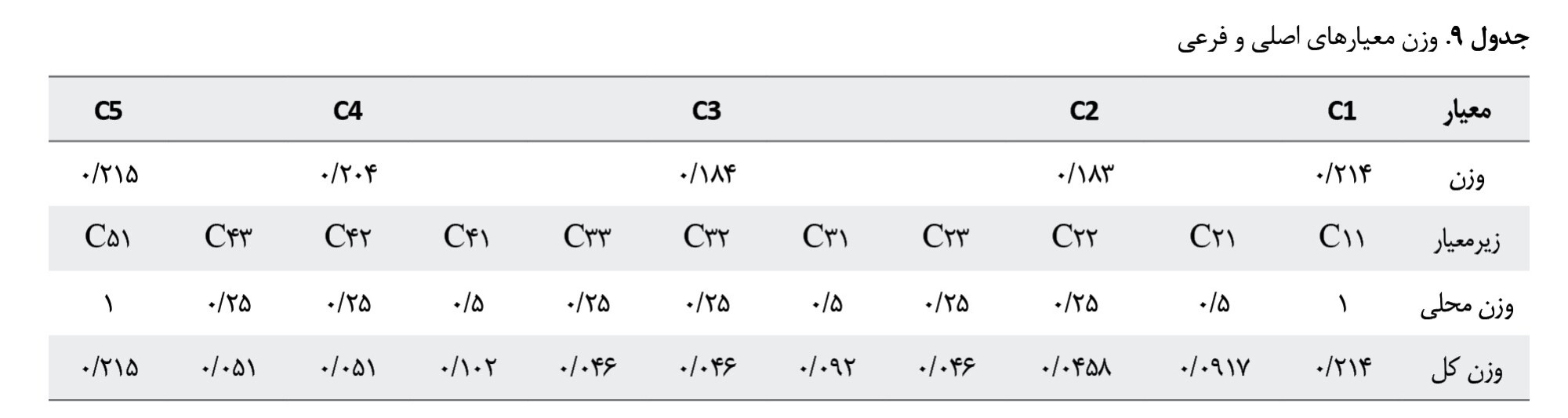
برای هر زیرمعیار، یک وزن محلی در نظر گرفته شده است که نشاندهنده اهمیت نسبی آن زیرمعیار نسبت به سایر زیرمعیارهای همان معیار اصلی است. در
جدول شماره 9 وزن محلی زیرمعیارها بهصورت تصادفی در نظر گرفته شده است و مجموع آنها باید 1 شود.
وزن کلی هر زیرمعیار با ضرب وزن محلی آن در وزن معیار اصلی مربوطه محاسبه میشود. این وزن، اهمیت نهایی هر زیرمعیار را در کل سیستم نشان میدهد. پس از محاسبه وزن کلیه معیارهای اصلی، میتوان وزن کلی هر زیرمعیار را با استفاده از فرمول شماره 10 محاسبه کرد. نتایج محاسبات در
جدول شماره 9 نشان میدهد که معیار ظرفیت گره» بیشترین اهمیت را در تصمیمگیری دارد و درنتیجه، افزایش ظرفیت گرهها، تأثیر بسزایی در بهبود عملکرد سیستم خواهد داشت. همچنین، زیرمعیار برق در اغلب موارد، بیشترین وزن محلی را در بین زیرمعیارهای هر معیار اصلی دارد که اهمیت زیرساخت برق را در این مسئله تأیید میکند. با استفاده از این نتایج، میتوان اولویتبندی پروژههای توسعه شبکه را انجام داده و منابع را بهصورت بهینه تخصیص داد.
رتبهبندی گرههای حیاتی در شبکه زیرساختهای وابسته به یکدیگر آب و برق و فاضلاب با روش ارزیابی ریشه به شرح زیر انجام میشود:
گام اول: تشکیل ماتریس تصمیمگیری R
در
جدول شماره 10 ماتریسی تشکیل میشود که در سطرهای آن 21 گره شبکه و در ستونهای آن معیارهای مختلف (با در نظر گرفتن زیرمعیارها) قرار میگیرند. مقادیر هر سلول از این ماتریس، نشاندهنده میزان برآوردهسازی هر معیار توسط هر گره است. در ساخت ماتریس تصمیمگیری در روش ارزیابی ریشه، معیارها به دودسته اصلی سودمند و غیرسودمند تقسیمبندی شدند. معیارهای سودمند به مواردی اشاره دارند که افزایش آنها به بهبود عملکرد شبکه کمک میکند، درحالیکه معیارهای غیرسودمند، مواردی هستند که کاهش آنها مطلوب است. در این مطالعه، ظرفیت گره (C
1)، گره تأمین (C
2)، گره انتقال (C
3) بهعنوان معیارهای سودمند در نظر گرفته شدند. ارتباط با سایر شبکهها (C
4) و هزینه تعمیر (C
5) بهعنوان معیارهای غیرسودمند هستند. معیار هزینه به هزینههای مرتبط با تقویت یا تعمیر گرهها اشاره دارد و ارتباط به میزان وابستگی گره به سایر گرههای شبکه اشاره دارد. گرههایی که ارتباط بیشتری با سایر گرهها دارند، در صورت خرابی میتوانند تأثیر بیشتری بر کل شبکه بگذارند.
.jpg) گام دوم و سوم:نرمالسازی ماتریس تصمیمگیری و وزندار کردن آن
گام دوم و سوم:نرمالسازی ماتریس تصمیمگیری و وزندار کردن آن
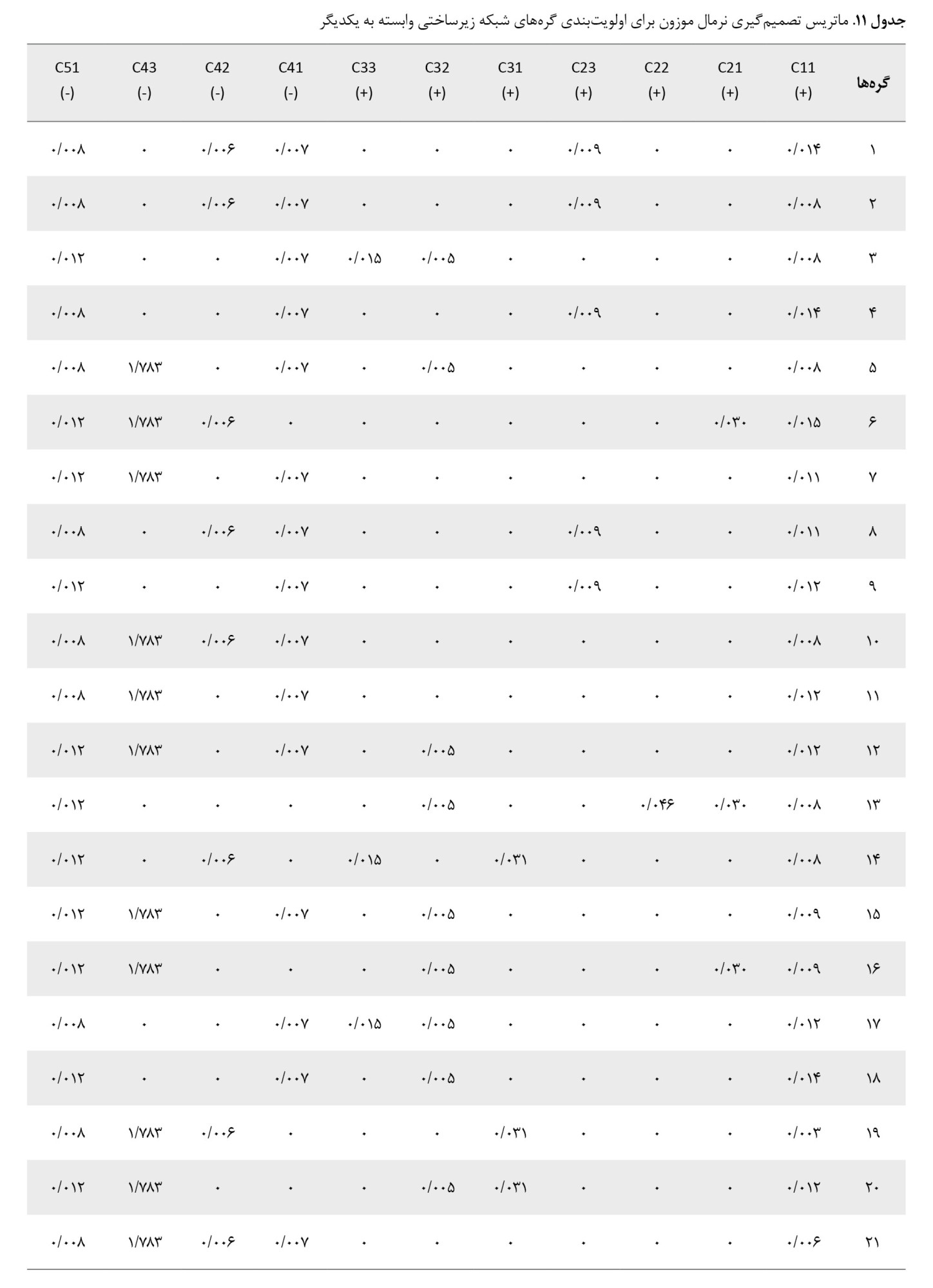
ماتریس تصمیمگیری ارائهشده در
جدول شماره 10 با استفاده از فرمول شماره 12 نرمال میشود. برای نرمالسازی، هر عنصر بر مجموع ستونی که این عنصر در آن قرار دارد تقسیم میشود. با ضرب ماتریس نرمالسازی شده در ماتریس وزن معیارها و به کمک فرمول شماره 13 ماتریس تصمیمگیری وزنی حاصل میشود. این نتایج در
جدول شماره 11 نشان دادهشده است.
 گام چهارم
گام چهارم
برای هر گزینه مجموع مقادیر وزنی نرمال شده برای معیارهای سودمند () و معیارهای غیرسودمند () محاسبهشده است. امتیاز کلی هر گزینه با استفاده از فرمول شماره 16 به دست آمده است و سپس گزینهها براساس مقادیر رتبهبندی شده است. نتایج رتبهبندی تولیدشده توسط روش ارزیابی ریشه در
جدول شماره 12 ارائه شده است. مشخص شد که در شبکه زیرساختهای وابسته به یکدیگر آب، برق و فاضلاب، گرههای 12، 13، 15، 5 و 6 بهترتیب بیشترین اهمیت را دارند. این گرهها باید در اولویت اول برای تقویت و بهبود قرار گیرند تا تابآوری کل شبکه در برابر بحرانهای احتمالی افزایش یابد. ازسویدیگر، گرههای 11، 19 و 10 کمترین اهمیت را در شبکه دارند. نکته قابلتوجه این است که تفاوت در مقادیر نرمالشده بین گرههای مختلف نسبتاً کم است، که نشان میدهد اهمیت نسبی گرهها در این شبکه به هم نزدیک است. این یافتهها میتواند به مدیران و تصمیمگیرندگان کمک کند تا منابع محدود را بهطور مؤثرتری برای تقویت نقاط حیاتی شبکه تخصیص دهند و درنتیجه، تابآوری کلی سیستم را در برابر اختلالات احتمالی بهبود بخشند.
نتایج حاصل از تحلیل
جدول شماره 12 نشان میدهد که گرههای حیاتی شناساییشده در رتبهبندی، معمولاً گرههایی هستند که در چندین زیرساخت نقش کلیدی دارند یا وابستگیهای زیادی به سایر گرهها دارند. این نشان میدهد که تقویت این گرهها میتواند بهطور قابلتوجهی به بهبود عملکرد کل شبکه کمک کند. علاوهبراین، وابستگیهای پیچیده بین زیرساختهای مختلف نشان میدهد که اختلال در یک زیرساخت میتواند تأثیر گستردهای بر عملکرد زیرساختهای دیگر داشته باشد. بنابراین، رویکردی جامع برای تقویت زیرساختها ضروری است که در آن تمام وابستگیها و تعاملات بین زیرساختها در نظر گرفته شود. پارامترهایی مانند ظرفیت، زمان تعمیر و هزینه تقویت نیز نقش مهمی در تعیین اهمیت گرهها دارند. گرههایی با ظرفیت بالا و زمان تعمیر کوتاه، اهمیت کمتری دارند، زیرا اختلال در آنها بهسرعت قابلجبران است. درنتیجه، برای افزایش تابآوری شبکه زیرساخت، پیشنهاد میشود که منابع محدود برای تقویت زیرساختها بر روی گرههای حیاتی شناساییشده متمرکز شود. این گرهها معمولاً گرههای انتقال یا تأسیسات اصلی هستند که اختلال در آنها میتواند تأثیر گستردهای بر کل شبکه داشته باشد. همچنین، باید به وابستگیهای بین زیرساختها توجه ویژه شود و اقدامات لازم برای کاهش این وابستگیها انجام شود.
.jpg) نتیجهگیری
نتیجهگیری
در این تحقیق، با استفاده از روشها و تحلیلهای جامع، به بررسی معیارهای مختلف در ارزیابی و تقویت شبکههای زیرساختی بحرانی پرداخته شد. روش دیمتل برای تعیین وزن معیارهای مختلف مورداستفاده قرار گرفت و مشخص شد که ظرفیت گره مهمترین معیار در ارتقاء عملکرد و پایداری شبکه است. این معیار، بهعنوان تأثیرگذارترین عامل، نقش کلیدی در مدیریت و بهبود شبکههای زیرساختی داشت. روش ارزیابی ریشه به شناسایی و رتبهبندی گرههای حیاتی کمک کرد. نتایج نشان داد که گرههایی با ظرفیت بالا و تأثیر زیاد بر شبکه، ازجمله گرههای شماره 5، 6، 13، و 15 بهعنوان نقاط بحرانی شناخته شدند که نیازمند توجه و تقویت بیشتری هستند. این گرهها در صورت بروز خرابی، میتوانند تأثیرات گستردهای بر کل شبکه داشته باشند و بنابراین، اولویتبندی دقیق آنها برای تخصیص منابع و اجرای برنامههای بهبوددهنده ضروری است. تقویت گرههای شناساییشده و بهینهسازی زیرساختها میتواند بهطور قابلتوجهی تابآوری و پایداری شبکههای زیرساختی بحرانی را افزایش دهد. چراکه شناخت و تحلیل وابستگیهای متقابل بین گرههای شبکههای زیرساختی آب، فاضلاب و برق برای بهبود پایداری و تابآوری این شبکهها ضروری است. با شناسایی گرههای بحرانی و تقویت آنها، میتوان از وقوع اختلالات گسترده جلوگیری کرد و عملکرد پایدار شبکه را تضمین نمود. این موردی است که در تحقیقات پیشین بدان پرداخته نشده است و در این پژوهش مورد توجه قرار گرفته است.
محدودیت های پژوهش
برخی از دادههای مطالعه موردی در منبع اولیه (
سوتچین و همکاران، 2023) موجود نبود و از طریق منابع دیگر نیز قابل دسترسی نبود لذا مجبور شدیم از دادههای تصادفی برای آنها کمک بگیریم.
پیشنهادهای آتی
همچنین، این پژوهش با ارائه یک چارچوب جامع برای تحلیل و ارزیابی شبکهها، زمینهای برای تحقیقات بیشتر و توسعه روشهای پیشرفتهتر در این حوزه فراهم میکند. پیشنهادهای آتی شامل گسترش مدلسازی، استفاده از دادههای واقعی، تحلیلهای بینرشتهای، و توسعه ابزارهای تصمیمگیری چند معیاره است. این پیشنهادها میتواند به بهبود و تقویت شبکههای زیرساختی بحرانی کمک کند و همچنین، موجب ارتقاء دانش و فناوری در این زمینه شود.
ملاحظات اخلاقی
پیروی از اصول اخلاق پژوهش
از اصول اخلاق در پژوهش استفاده شده است و از دادههای محرمانه نیز استفاده نگردیده است.
حامی مالی
این مقاله برگرفته از رساله دکتری آذر احرامباف شوشتر است و هیچگونه کمک مالی از سازمانیهای دولتی، خصوصی و غیرانتفاعی دریافت نکرده است.
مشارکت نویسندگان
مفهومسازی: آذر احرامباف، پروانه سموئی و معصومه مسی بیدگلی؛ تحقیق و بررسی: آذر احرامباف، پروانه سموئی و معصومه مسی بیدگلی؛ ویراستاری و نهاییسازی نوشته: پروانه سموئی و معصومه مسی بیدگلی.
تعارض منافع
بنابر اظهار نویسندگان، این مقاله تعارض منافع ندارد.









































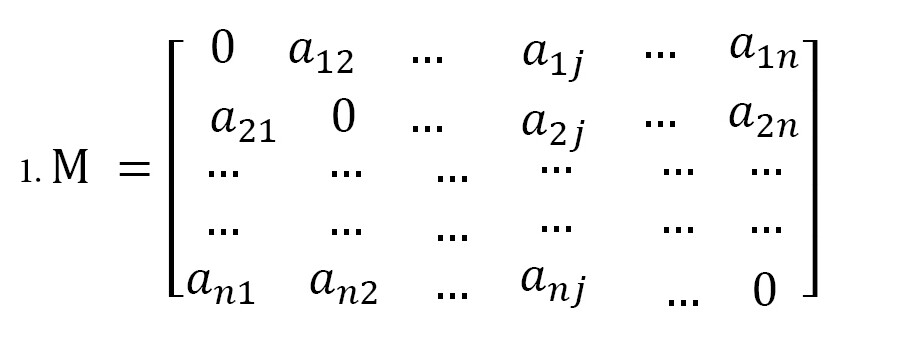
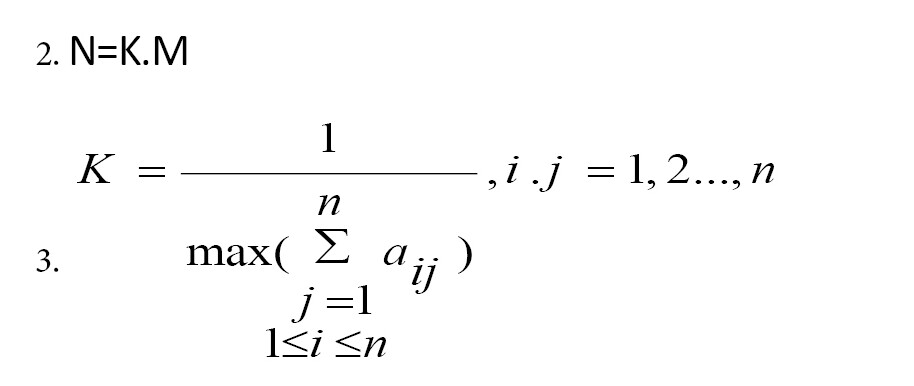
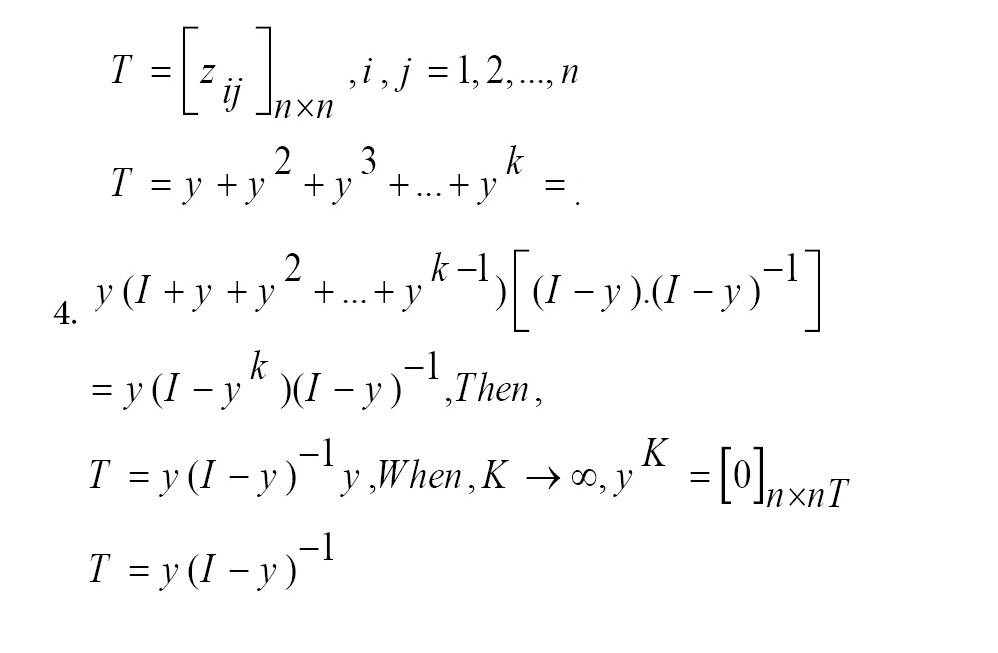

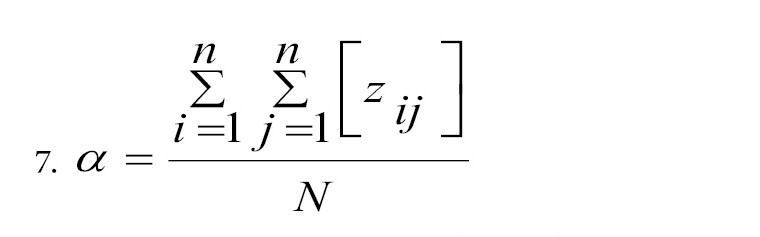
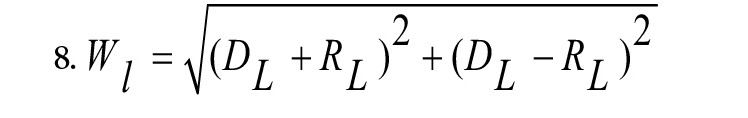
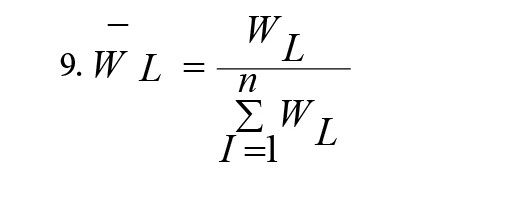
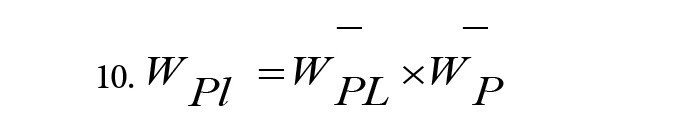
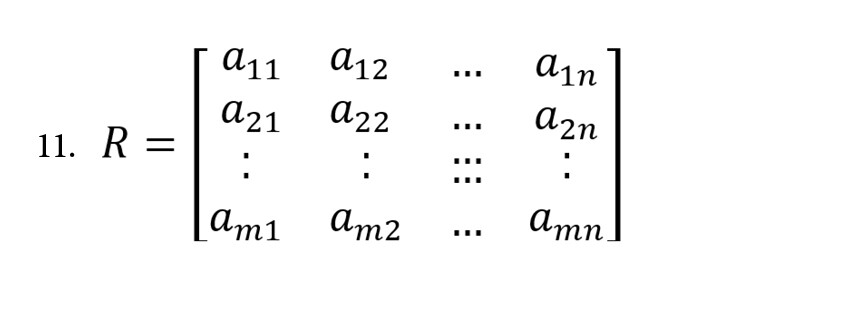
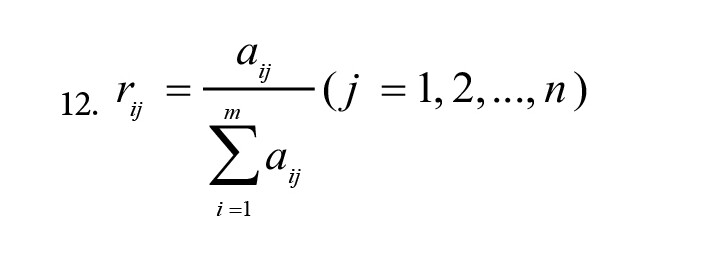
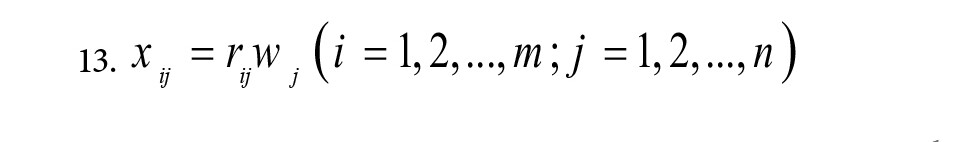
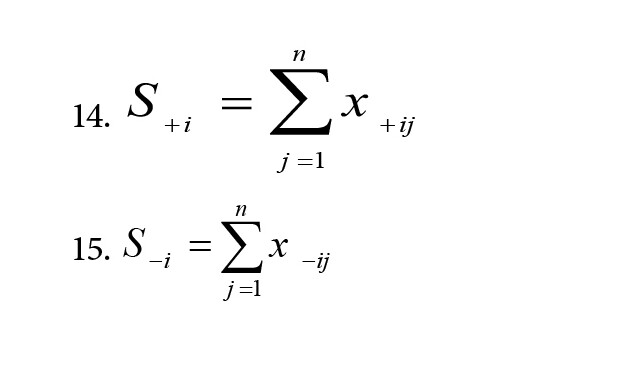
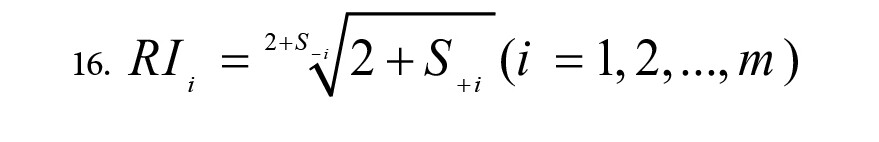










.jpg)

.jpg)
