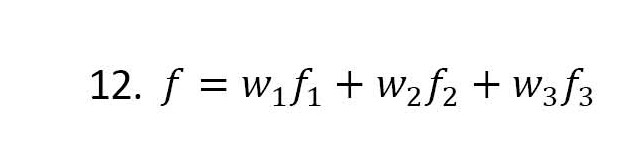مقدمه
در دهههای اخیر، سوانح طبیعی اثرات مخربی را برای مردم به همراه داشته است. این سوانح طبیعی مکرراً آسیبهای جدی به حیات انسان وارد میکنند و خسارات اقتصادی هنگفتی را به همراه دارد (
دانشور و همکاران، 2023). براساس گزارش سازمان ملل، بین سالهای 1998 تا 2017، 1/3 میلیون نفر کشته و 4/4 میلیارد نفر مجروح، بیخانمان، آواره یا نیازمند کمکهای اضطراری بودهاند. در طول این سالها 563 زمین لرزه، 56 درصد از کل تلفات را به خود اختصاص داده است که براساس آن 747234 نفر در جهان جان خود را از دست دادهاند (
رضایی و همکاران، 2021). سازمان بینالمللی کاهش سوانح طبیعی سازمان ملل تخمین زده است که هزینه واقعی بلایا ازجمله زلزله بین 250 تا 300 میلیارد دلار در سال است. بنابراین مردم توجه بیشتری به مدیریت اضطراری بلایا بهویژه چگونگی کاهش تلفات مکانهای آسیبدیده، تلفات و تضمین بقای افراد آسیبدیده دارند (
وانگ و همکاران، 2023).
علاوه بر اینکه وقوع بلایا هزینهزا هستند، بسیاری از بلایا غیرقابلپیشبینی هستند که باعث تلفات سنگین، خسارات مالی، آسیب به محیطزیست محیطی و آسیبهای اجتماعی جدی شدهاند یا احتمالاً به آن منجر میشوند (
وانگ و همکاران، 2021). تصمیمگیری برای تخصیص مکان سرپناه بر موفقیت واکنش در بلایا و تأمین امنیت لازم برای قربانیان تأثیر میگذارد. برای مثال، بحرانی اخیراً دنیا را تحتالشعاع خود قرار داده است؛ در اواخر سال 2019 در چین ویروس جدید کووید ـ 19 منتشر شد و دنیا را در یک بحران بهشدت سخت قرار داد که باعث بیشترین مرگومیر نسبت به دهههای قبل شد (
جهانگیری و همکاران، 2021). همچنین براساس دادههای آماری سوانح طبیعی گزارششده توسط مرکز تحقیقات اپیدمیولوژی، سوانح طبیعی، مانند زلزله و سیل در کنار تمام بحرانهای ساختهشده توسط انسان شایعترین فجایع بودهاند که تا سال 2019 براساس موارد مشاهدهشده باعث شدهاند 5110 نفر کشته شوند (
، 2019). در این میان، لجستیک بشردوستانه نقش مهمی در تسهیل فرایندهای مدیریت بلایا و تخلیه قربانیان از مناطق آسیبدیده به مکانهای امن و با برنامهریزی، ذخیره و توزیع تجهیزات کمکی برای کمک به قربانیان در زمان، مکان مناسب و هزینه مناسب ایفا میکند (
جهانگیری و همکاران، 2021). این در حالی است که منابع محدود یک مشکل بزرگ در زنجیره تأمین بشردوستانه ایجاد میکند.
در هنگام وقوع گسترده بحران، بیانصافی است که به یک منطقه اولویت بیشتری داده شود و خدمات بیشتر را دریافت کند (
چوبر و همکاران، 2022). در همین حال، منطقه دیگری به دلیل کمبود عرضه، کمتر از سهم منصفانه خود خدمات دریافت کند (
یوفریدو و هارجانا، 2019). بنابراین تصمیمگیریهای اخلاقی برای تصمیمگیرندگان چالشبرانگیز است، اما زمانی که بستههای معیشتی برای ارضای همه تقاضاها کافی نیستند، این شرایط نیازمند رویکرد تخصیصی مناسب است تا بتوان اقلام امدادی را بهگونهای به مناطق آسیبدیده تخصیص داد که اولویت یکسانی برای برآوردن نیازهای بخشهای مختلف جمعیت آسیبدیده در نظر گرفته شود (
گوپتا و رانگانتان، 2006).
باتوجهبه این واقعیت که مناطق مختلف نیازهای متفاوتی دارند، رفتار منصفانه بهعنوان برخورد در تحقق میزان تقاضا یا مقابله با میزان کمبود در تقاضا تعریف میشود. بنابراین با استفاده از زنجیره تأمین بشردوستانه پس از وقوع یک فاجعه، با بهرهگیری از لجستیک اضطراری باید بتوان کالاهای امدادی را در تمام نقاط بحران در یک رویه عادلانه توزیع کرد (
ژنگ و همکاران، 2015). دراینصورت به همان نسبت تقاضا، باید اقلام یا کالاهای امدادی به نقاط آسیبدیده مورد تقاصا اختصاص یابند. بهعبارتدیگر، اگر منابع امدادی محدود باشند، ممکن است بهتر باشد برآورده کردن بخشی از نیازهای مناطق آسیبدیده بهجای برآورده کردن کامل تقاضاهای یک نقطه تقاضا و نادیده گرفتن کامل آن در نقطه دیگر، ارجح باشد (
آنایا و همکاران، 2018).
تعیین محل تخصیص تسهیلات برای مقابله با حوادث بلایا بهدقت توسط تصمیمگیرندگان مورد توجه قرار گرفته است. مطالعات متعددی معمولاً بر روی مدلهای بهینهسازی تکهدفه یا روشهای محاسباتی مسائل چندهدفه برای تعیین جوابهای مغلوب و نامغلوب در تلاش برای بهبود کارایی و اثربخشی تدارکات امدادرسانی بشردوستانه پیشنهاد شده است. این امکانات شامل سرپناه، مراکز پزشکی، انبارها، مراکز توزیع، کنترل و پیشگیری از بیماریها و دفع ضایعات هستند (
بونمی و همکاران، 2017). در میان این تحقیقات، برخی از مطالعات شامل قضاوتهای ذهنی هستند که در آن تصمیمگیرندگان ترجیحات خود را تعریف میکنند (
رو و همکاران، 2018؛
رو و همکاران 2013). ادبیات موجود براساس فرمولبندی مدل، سطوح زنجیره تأمین، تابع هدف، انواع تسهیلات، راهحلها و مطالعه موردی بررسی و گروهبندی شده است. در این طبقهبندی، تابع هدف به سوددهی و غیرسوددهی طبقهبندی شده است.
باتوجهبه بررسی پیشینه تحقیق، اکثر مقالات موجود مدلهای بهینهسازی تکهدفه را برای بهبود معیارهای سوددهی یا غیرسوددهی، مانند به حداقل رساندن تعداد سرپناهها و حل مسئله مدل با الگوریتم دقیق توسط
اوزبای و همکاران (2019) پیشنهاد کردهاند. به حداقل رساندن هزینه کل مکانیابی ـ تخصیص سرپناه و استفاده از الگوریتم ژنتیک در حل این مدل توسط
پرانیتفولکرانگ و هوین (2020) ارائه شده است و به حداکثر رساندن رضایت تصمیمگیرندگان و حل مدل فرمولهشده با استفاده از برنامهریزی آرمانی وزندارشده توسط
کانون و همکاران (2010) معرفی شده است. اکثر این مطالعات از روشهای تخصیص وزن (یعنی برنامهریزی آرمانی وزندارشده و روش تابع هدف وزندارشده) برای پرداختن به روشهای محاسباتی مسائل چندهدفه استفاده میکنند. این روشها برای استفاده در حوزه لجستیک بشردوستانه مناسب نیست. این باعث میشود تصمیمگیرندگان در هنگام تصمیمگیری درمورد اینکه کدام معیار مهم است، دچار اشتباه شوند. برخی از مهمترین مطالعاتی که اخیراً در این حوزه منتشر شدهاند را در ادامه بهطور خلاصه معرفی میکنیم.
برای مثال،
ماهارجان و هانائوکا (2019)، یک مدل تخصیص مکان چندهدفه تحت عدم قطعیت برای عرضه و توزیع بشردوستانه ایجاد کردند. مدل ارائهشده، اهداف به حداقل رساندن هزینه کل و به حداکثر رساندن پوشش تقاضای کل را در نظر میگیرد. برای حل مدل از روش اپسیلون محدودیت استفاده شده است. آبیشک
بهل و همکاران (2019)، در مطالعه خود، عوامل موفقیت مهم در مدیریت زنجیره تأمین بشردوستانه را با استفاده از رویکرد دیمتل خاکستری، با هدف تثبیت هدف اصلی بررسی عوامل موفقیت مهم برای مدیریت زنجیره تأمین بشردوستانه در هند ازطریق مرور سیستماتیک ادبیات بررسی کردند.
دورا و کومار (2020)، در مطالعه خود برنامههای بهبود عملیاتی و عملیات بشردوستانه را در مواجهه با پاندمی کرونا ارائه کردند.
جیانگ و همکاران (2020)، ارزیابی عوامل مهم تأثیرگذار بر قابلیت اطمینان سیستمهای لجستیک اضطراری را با استفاده از روش تصمیمگیری دیمتل و تحلیل شبکهای انجام دادند.
آگراوال و همکاران (2020)، در مقاله خود ارزیابی راهحلهای غلبه بر موانع مدیریت زنجیره تأمین بشردوستانه را با استفاده از یک روش ترکیبی سوارا فازی ـ واسپاس فازی، برای مدیریت زنجیره تأمین بشردوستانه ارائه دادند.
آقاجانی و همکاران (2020)، یک مدل محاسباتی دوهدفه تحت عدم قطعیت برای یک زنجیره تأمین امداد بشردوستانه پیشنهاد کردند. شبکه پیشنهادی برای به حداقل رساندن هزینه کل و به حداکثر رساندن تقاضا در نظر گرفته شده است. برای حل مدل از روش اپسیلون محدودیت وزندارشده استفاده شده است.
مغفیرو و همکاران (2020)، یک مدل توزیع عرضه بشردوستانه چندوجهی را با در نظر گرفتن حالتهای مختلف حملونقل که تمایل دارند زمان تحویل کل و هزینه کل شبکه را به حداقل برسانند، توسعه دادند.
منصوری و همکاران (2020)، یک مدل دوهدفه برای زنجیره تأمین بشردوستانه پیشنهاد کردند. در این مطالعه، تدارکات امدادی در شرایط عدم قطعیت با هدف به حداقل رساندن تعداد کل قربانیانی که تخلیه یا به بیمارستان منتقل نمیشوند و به حداقل رساندن کل تقاضاهای برآوردهنشده انجام میشود. پارامترهای زمان سفر و تقاضا تحت عدم قطعیت در نظر گرفته میشوند. سپس مدل ارائهشده با استفاده از روش چبیشف وزندارشده حل شده است.
صبوحی و همکاران (2020)، یک مدل برنامهریزی تصادفی 2 مرحلهای برای مدیریت زنجیره تأمین بشردوستانه با در نظر گرفتن عدم قطعیت و اختلالات پیشنهاد کردند. تصمیمگیری درمورد مکان مراکز توزیع و تصمیمگیری درمورد زمانبندی و مسیریابی به ترتیب در مرحله اول و دوم رویکرد پیشنهادی اتخاذ میشود.
ممشلی و همکاران (2021)، در مطالعه خود یک مدل برنامهریزی چندهدفه مبتنی بر سناریو را برای بررسی مسئله تخصیص مسیریابی پایدار ـ تابآور با در نظر گرفتن مفهوم زنجیره تأمین بشردوستانه پیشنهاد کردند. هدف مدل پیشنهادی به حداقل رساندن کل زمان سفر، اثرات کل زیستمحیطی و از دست دادن کل تقاضاست. رویکرد بهینهسازی تصادفی استوار فازی برای مقابله با دادههای نامشخص در شرایط فاجعه استفاده میشود.
جهانگیری و همکاران (2021)، در مطالعه خود به ارزیابی عناصر زنجیره تأمین بشردوستانه برای پیادهسازی موفقیتآمیز آن در بیمارستانهای ایران از یک روش ترکیبی تصمیمگیری مبتنی بر تاپسیس و بهترین ـ بدترین استفاده کردهاند. در این مطالعه با تعیین اهمیت هریک از شاخصهای اثرگذار بر روی منابع با استفاده از روش بهترین ـ بدترین، اولویتبندی منابع کلیدی با استفاده از روش تاپسیس انجام شده است.
رضایی و همکاران (2021) در مطالعه خود به یک مسئله مسیریابی وسایل نقلیه امدادرسان برای خونرسانی در وقوع فاجعه در زمان بروز زلزله پرداختهاند. در این مطالعه یک مسئله چندهدفه بهمنظور کنترل حداکثر مقدار خون جمعآوریشده در کمترین زمان ممکن با استفاده از یک مسئله برنامهریزی عدد صحیح مختلط ارائه شده است.
میرزاپور آل هاشم و همکاران (2022) در مطالعه خود یک مدل ریاضی برای زمانبندی برداشت و تحویل اعضای پیوندی و مسیریابی آمبولانسهای حامل اعضا و بیماران پیوندی، بهعنوان حلقه پایانی زنجیره تأمین پیوند اعضا در شهر تهران ارائه دادهاند. مسئله در قالب یک برنامهریزی غیرخطی عددصحیح مختلط فرمولهشده و در ادامه با استفاده از روشهای دقیق به یک مدل ریاضی خطی معادل تبدیل شده است. مدل ارائهشده به دنبال یافتن زمانبندی و توالی بهینه برداشت و تحویل اعضا و بیماران، باتوجهبه محدودیتهای عملیاتی نظیر زمان ایسکمی سرد، ترافیک شهری و نیز محدود بودن ناوگان حمل است. مدل پیشنهادی با استفاده از نرمافزار سیپلکس 12/8 بهصورت بهینه حل شده و نتایج محاسباتی بر کاربردپذیری آن صحه میگذارد.
ونگ و همکاران (2021) یک مدل برنامهریزی عدد صحیح مختلط براساس هزینه زمانی تحت عدم قطعیت پیشنهاد کردهاند. مدل ارائهشده به حل مسئله مکانیابی و توزیع انبار اضطراری کمک میکند. در نظر گرفتن عواملی مانند هزینه زمان، هزینه جریمه برای کمبود منابع، در نظر گرفتن منابع جایگزین از هر تأمینکننده و سرپناههای اضطراری، وسایل حملونقل مختلف و انواع منابع متعدد در این مطالعه دخیل هستند. همچنین سناریوهای نامشخصی برای توصیف شدت فاجعه معرفی شدهاند. برای حل مسئله از بهینهسازی ازدحام ذرات و جستوجوی همسایگی متغیر برای حل مدل برنامهریزی عدد صحیح مختلط در مقیاسهای مختلف مورد استفاده قرار گرفته است.
کائو و همکاران (2021)، در این تحقیق یک مدل برنامهریزی اعداد صحیح 2 سطحی 3 هدفه فازی برای به حداقل رساندن نرخ تقاضای برآوردهنشده، خطرات زیستمحیطی بالقوه، هزینههای اضطراری در سطح بالای سلسلهمراتب و به حداکثر رساندن رضایت درکشده بازماندگان در سطح پایین سلسلهمراتب را فرموله میکنند. یک روش بهینهسازی معیار سراسری ترکیبی برای ترکیب یک الگوریتم، بهمنظور محاسبه ارزش موردانتظار معرفی شده است.
سونو راجاک و همکاران (2021)، در مقاله خود عوامل موفقیت مهم برای ابتکارات پایدار در زنجیره تأمین در طول شیوع همهگیری کووید ـ 19در هند را تجزیهوتحلیل کردند. تجزیهوتحلیل و رتبهبندی براساس استقرار عملکرد ترکیبی کیفیت و روش بهترین ـ بدترین انجام شده است.
پاتیل و همکاران (2021)، در مطالعهشان مدیریت محصولات پزشکی را بررسی کردهاند و اتخاذ شیوههای پایداری را در زنجیره تأمین پزشکی که زنجیره تأمین بشردوستانه را تسهیل میکند بیان کردهاند.
شائو هانگ و همکاران (2022)، در مطالعه خود یک الگوریتم مکانیابی ایستگاه برای انتقال کالا ارائه میدهند. این روش براساس الگوریتم نزدیکترین همسایه معکوس و مشخصههای چگالی محلی است. ابتدا مکان ایستگاه انتقال در منطقه را غربال میکند تا براساس تراکم از فاصله مناسب، مکان و محدوده پوشش آن را تعیین کند. درنهایت با محاسبه شاخصهای لازم هر ایستگاه در ناحیه توزیع، مرز ناحیه توزیع مجدداً تعریف میشود.
پنگ و همکاران (2022)، یک مدل مکانیابی مراکز منابع اضطراری با هدف فاصله وزنی کل ایجاد کردند. سپس یک بهینهسازی ازدحام ذرات گسسته جدید چندهدفه را برای آن طراحی کردند. درنهایت، آزمایشهای عددی الگوریتمهای مقایسه و آزمایشهای فرسایشی بر روی ۲۶ مجموعه داده انجام میشود تا اثربخشی و سراسری بودن الگوریتم پیشنهادی را نشان دهد.
پورناصر و همکاران (2022) یک مدل بهینهسازی چندهدفه برای مسیریابی در حین وقوع بحران ارائه دادهاند. در این مطالعه یک تابع هدف در راستای کاهش هزینهها و تابع هدف دیگر در راستای کاهش مدتزمان تعمیر وسایل نقلیه در نظر گرفته شده است. مسئله چندهدفه توسعهیافته با استفاده از روش اپسیلون محدودیت حل شده است.
دانشور و همکاران (2023) مسئله برنامهریزی طراحی و راهاندازی شبکههای زنجیره تأمین بشردوستانه را برای فاز پس از وقوع سوانح طبیعی در نظر گرفتهاند. بهطور خاص، یک شبکه 3 سطحی تحت تقاضا و عدم قطعیت ظرفیت برای حمایت از بازیابی کوتاهمدت برای توزیع منابع حیاتی بر جمعیت آسیبدیده تمرکز کردهاند. برای این منظور، یک مدل تصادفی 2 مرحلهای ایجاد شده است که عدم قطعیت مربوط به تقاضا را همراه با ظرفیتهای حملونقل و ذخیرهسازی در شبکه زنجیره تأمین بشردوستانه طراحی شده است.
وانگ و همکاران (2023) یک مدل بهینهسازی استوار مبتنی بر سناریو را برای ارائه طرحهای حملونقل مصدوم و استراتژیهای توزیع تجهیزات پزشکی پیشنهاد کردهاند. برای این منظور، 3 هدف بهینهسازی در مدل پیشنهادی، به حداقل رساندن هزینهها، انتشار کربن و موجودی در نظر گرفته شده است. مطالعه موردی براساس زلزله کرمانشاه، قابلیت اطمینان روش پیشنهادی را با بررسی احتمال اینکه نمونههای شبیهسازیشده استراتژیهای بهینهشده را نامعتبر نمیکنند، تأیید کرد.
براساس پیشینه تحقیق موجود، در این مقاله مسئله توزیع منصفانه اقلام ضروری از پایگاههای اضطراری به مناطق آسیبدیده در زمان وقوع بحران بررسی شد. اقلام امدادی به معنای کلیه اقدامات لازم اعم از عملیات خرید، آمادهسازی مواد و منابعی است که در هنگام، بعد و قبل از وقوع بحران نیاز است و باید در اختیار آسیبدیدگان قرار داده شود. برایناساس به دلیل محدودیت منابع یا افزایش هزینه در مدیریت صحیح زنجیره تأمین بشردوستانه، نمیتوان از نقاط بحران دوردست برای کمک چشمپوشی کرد، زیرا تقسیم اقلام معیشتی موردنیاز باید عادلانه صورت بگیرد. باتوجهبه اهمیت ذکرشده، در این مطالعه مسئله مکانیابی برای توزیع اقلام امدادی بهطور عادلانه ارائه شده است. مدل پیشنهادی در شهر تهران بهصورت کاربردی به کار گرفته شده است.
برای این منظور، با استفاده از توابع تعریفشده، مکانها و اقلام مناسب بر حسب تقاضا جهت ارسال اقلام امدادی و کمک معیشتی مانند سرپناهها، مراکز پزشکی، مراکز توزیع، انبارها، تعیین میشود. سپس برای واکنش مناسب به بلایا، تصمیمگیری درمورد نحوه تجهیز مکانها با استفاده از وسایل نقلیه و ازطریق ارسال اقلام مناسب انجام میپذیرد. مکان سرپناه و تسهیلات امدادرسان مهمتر از تصمیمگیری درمورد سایر اجزای زنجیره تأمین بشردوستانه است. زیرا طبق تدارکات بشردوستانه در حین وقوع بلایا، توزیع کالاهای امدادی در مکانهای متعدد مستلزم طیف جدیدی از سیاستها برای تخصیص بهینه و منصفانه اقلام امدادی به نقاط تقاضاست.
روش
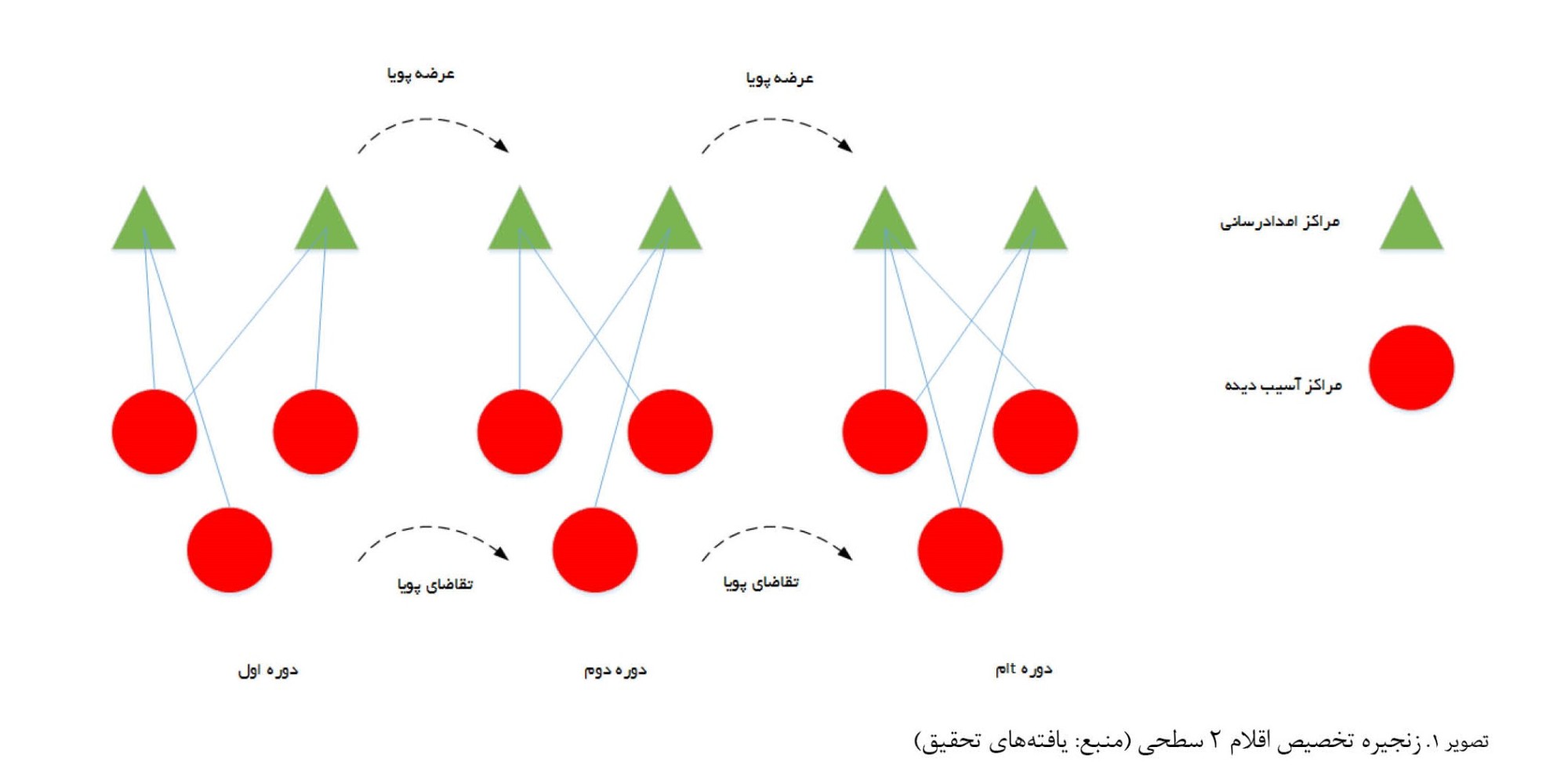
برای مقابله با بلایای مهیب، مانند زلزله میتوان مکانهایی را ایجاد کرد که در آن برای بازماندگان در سرپناهها مواد پزشکی، غذا و سایر ملزومات مهیا باشد. با وجود اینکه در حین بروز چنین اتفاقی مراکز مختلفی آسیب میبیند، تنها در نظر گرفتن یک مرکز امداد و نجات کافی نیست، در این مقاله یک مدل تخصیص مواد اضطراری بین مراکز امدادی مختلف و مکانهای آسیبدیده گوناگون معرفی شده است. در
تصویر شماره 1، شبکه تخصیص مواد ضروری 2 سطحی موردمطالعه در این مقاله نشان داده شده است. مطابق با
تصویر شماره 1، چند مرکز امدادی به مناطق مختلف سانحهدیده امدادرسانی میکنند. عرضه و تقاضا اقلام امدادی به آسیبدیدهها در هر دوره نسبت به دوره قبلی متفاوت است و ممکن است از هر دوره، عرضه یا تقاضای برآوردنشدهای باقی بماند که در دوره بعدی پوشش داده میشود. ازاینرو در این مقاله چارچوبی مبتنی بر مدلسازی ریاضی برای توزیع اقلام مختلف امدادرسانی از مراکز مختلف به نقاط آسیبدیده گوناگون ارائه میشود. در ادامه کلیه موارد اعم از متغیرها، پارامترها، توابع و محدودیتهای حاکم بر مدلسازی ریاضی توضیح داده شدهاند.
 مدلسازی ریاضی
مدلسازی ریاضی
مفروضات مدل
• امدادرسانی از مراکز امدادی مختلف به مراکز آسیبدیده گوناگون انجام میپذیرد.
• امدادرسانی با نسبت عادلانهای از موارد امدادی مشابه همراه است. بدینترتیب فرض میکنیم که به هر بازمانده، یک قلم کالای امدادی تعلق میگیرد.
• اقلام امدادی مختلفی برای امدادرسانی وجود دارد.
• دورههای زمانی مختلفی برای برنامهریزی در نظر گرفته شده که هر روز معادل 24 ساعت فرض شده است.
• پنجره زمانی برای اقلام امدادی در نظر گرفته شده است.
نمادگذاری
مجموعهها
L: مجموعه تمام مناطق آسیبدیده lϵL؛ P: مجموعه تمام مراکز امدادرسانی pϵP؛ T: کل دوره زمانی tϵT؛ Q: مجموعه انواع مختلف اقلام ضروری qϵQ.
پارامترها
s
pqt: مقدار عرضه برای مواد ضروری q در مراکز امدادی p در دوره t؛ D
lqt: تقاضا برای مواد ضروری q در سایت آسیبدیده l در دوره t؛ C
plt: هزینه دسترسی مراکز امدادی p به سایت آسیبدیده l در دوره t؛ C
plqt: هزینه انتقال واحد اقلام ضروری تخصیص دادهشده q از سایت امدادی p به سایت آسیبدیده l در دوره t؛ G
p: ارزش مواد ضروری q تخصیص دادهشده از مرکز امدادی p؛ w: ضریب تخصیص منصفانه اقلام؛ β
1: ضریب وزنی تابع هدف اول؛ β
2: ضریب وزنی تابع هدف دوم؛ β
3: ضریب وزنی تابع هدف سوم؛ [l
q; u
q]: پنجره زمانی تحویل اقلام ضروری q.
متغیرها
d
plqt: مرکز امدادی p مقدار اقلام ضروری q را به منطقه آسیبدیده l در دوره t اختصاص می دهد؛ u
lqt: تقاضای برآوردهنشده برای اقلام ضروری q در منطقه آسیبدیده l در طول دوره t؛ Q
plt: مقدار کل مواد تحویل دادهشده از مرکز امدادی p به منطقه آسیبدیده l در دوره t؛ r
lqt: نرخ رضایت تقاضا برای اقلام ضروری q در منطقه آسیبدیده l در طول دوره t؛ û
lqt: نرخ رضایت ایدئآل تقاضا برای اقلام ضروری q در منطقه آسیبدیده l در طول دوره t؛ ũ
lqt: نرخ تقاضای برآوردهنشده برای اقلام ضروری q در منطقه آسیبدیده l در طول دوره t؛ v
plt: متغیر باینری اگر مرکز امدادی p اقلام را به منطقه آسیبدیده اختصاص دهد برابر با 1 و در غیر اینصورت صفر است.
توابع هدف و محدودیتها
فرمولهای شماره 1-10:

فرمول شماره 1 تابع هدف اول مسئله است و به حداقل رساندن هزینه حملونقل که از هزینه حمل ثابت و واحد تشکیل شده است را تضمین میکند. فرمول شماره 2 تابع هدف دوم مسئله است که به حداقل رساندن نرخ تقاضای برآوردهنشده هر مرکز آسیبدیده در کل دوره را تضمین میکند. با استفاده از این تابع هدف میتوانیم حداکثر مطلوبیت تقاضاکنندگان را درصورتیکه تقاضای برآوردهنشده کمینه شود، بیشینه کنیم. فرمول شماره 3 به حداقل رساندن فاصله بین نرخ برآورد تقاضا و نرخ رضایت ایدئال از هر مرکز آسیبدیده در کل دوره را تضمین میکند. فرمول شماره 4 جمع وزنی 3 تابع هدف را با هم ترکیب میکند. فرمول شماره 5 محدودیت تقاضاست که هدف آن این است که تضمین میکند که مقدار مواد امدادی تخصیص داده شده کمتر از تقاضا نباشد. فرمول شماره 6 محدودیت عرضه است که میتواند تضمین دهد مقدار مواد تخصیصیافته به مراکز امدادی در هر دوره از مقدار مواد قابلتخصیص تجاوز نمیکند. در صورت وجود مواد تخصیص دادهنشده باقیمانده، میتوان آنها را در دوره بعدی تخصیص داد. فرمول شماره 7 برای به حداکثر رساندن محدودیت رضایت تقاضا است؛یعنی اگر عرضه دوره بیشتر از تقاضا باشد، تمام تقاضاها برآورده میشود. اگر تقاضا برای دوره بیشتر از عرضه باشد، تمام عرضه توزیع میشود. فرمول شماره 8 به این اشاره دارد که اگر یک مرکز امدادی تصمیم بگیرد که مواد را در یک مکان آسیبدیده در یک دوره معین توزیع کند، هزینههای حملونقل مربوطه باید پرداخت شود؛ یعنی محدودیتهای ظرفیت حملونقل برقرار است. فرمول شماره 9 تضمین میکند که مقدار کل مواد تحویل دادهشده از مراکز امدادی به مناطق آسیبدیده در پنجره زمانی در نظر گرفتهشده توزیع شود. فرمول شماره 10 تضمین میکند که متغیر تخصیص اقلام به مناطق آسیبدیده یک متغیر باینری است. فرمول شماره 11 تضمین میکند که مقدار اقلام اختصاص دادهشده به مناطق آسیبدیده یک متغیر پیوسته است.
روش حل مسئله
در این مقاله از روش مجموع وزندارشده برای حل مسئله و یافتن جواب بهینه استفاده شده است. این روش یک روش بهینهسازی چندهدفه است که در آن چند هدف وجود خواهند داشت و باید بهترین راهحل را تعیین کنیم. براساس این روش، تمام توابع چندهدفه را با استفاده از مجموع وزنی مطابق با فرمول شماره 12 در تابع هدف ترکیبی با هم ترکیب و تبدیل به یک مسئله تکهدفه میکنیم.
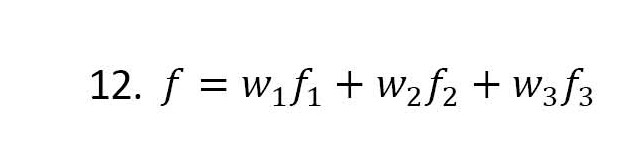
یک مسئله مهم در تخصیص بردار ضرایب وزنی w1,…,wn در روش مجموع وزندارشده این است که این وزنها مثبت هستند و مجموع آنها برابر با یک است علاوهبراین، راهحل بهینه بهشدت به ضرایب وزنی انتخابشده بستگی دارد و در صورت تغییر آنها مقدار تابع هدف ترکیبی تغییر میکند. بنابراین همواره باید مقداری انتخاب شود که مقدار تابع هدف ترکیبی را بدتر نکند (
رضایی و همکاران، 2021).
یافتهها
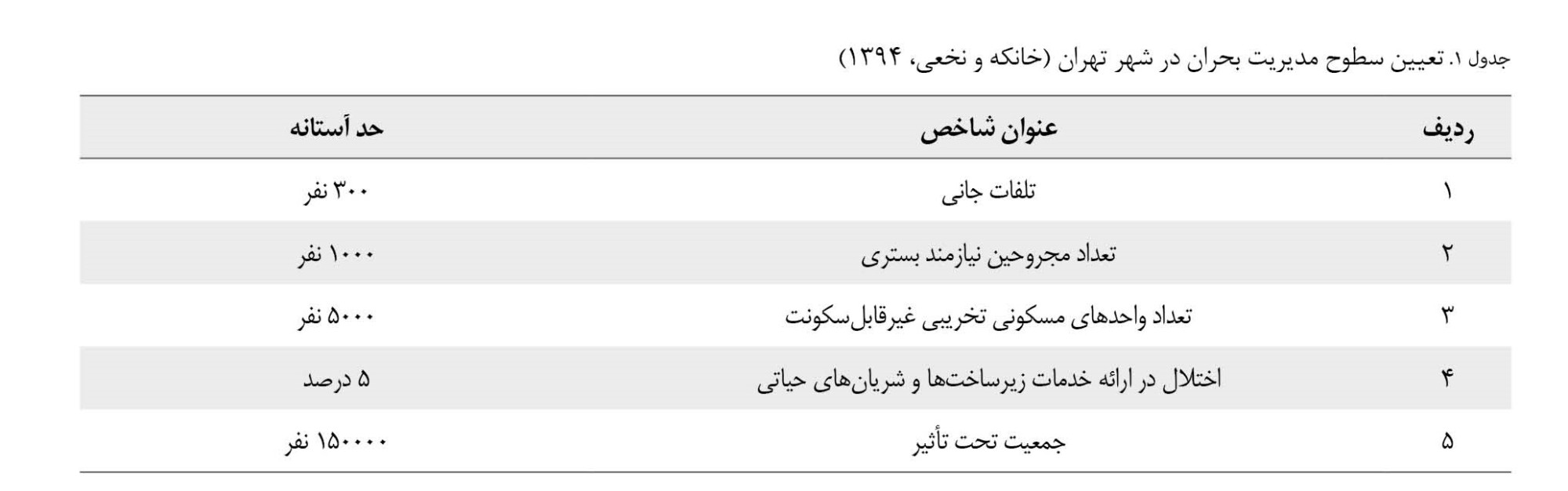
باتوجهبه شرایط ویژه و اهمیت شهر تهران بهعنوان پایتخت جمهوری اسلامی ایران و وجود مراکز حساس ملی در آن، حوادث شهر تهران به 2 سطح محلی و ملی تقسیم میشود و تشخیص حادثه محلی در شهر تهران براساس شاخصهای ارائهشده در دستورالعمل نحوه تعیین سطوح و شیوه اعلام بحرانها به شماره 170018 مورخه 24/12/1395 وزارت کشور مطابق
جدول شماره 1 تعیین شده است؛ چنانچه براساس اطلاعات دریافتی مقادیر 3 شاخص از 5 شاخص
جدول شماره 1 بیش از ارقام حد آستانه باشد سطح حادثه ملی خواهد بود.
باتوجهبه وقوع بحران در کلانشهر تهران، ستاد مدیریت بحران این شهر مطابق با تبصره 1 ماده 10 قانون، به ریاست وزیر کشور و جانشینی شهردار تهران، دبیری رئیس سازمان پیشگیری و مدیریت بحران شهر تهران، فرماندار و استاندار تهران تشکیل میشود. ساختار ستاد پیشگیری، هماهنگی و عملیات پاسخ به بحران در تهران مطابق با سلسلهمراتب موجود در
تصویر شماره 2 است
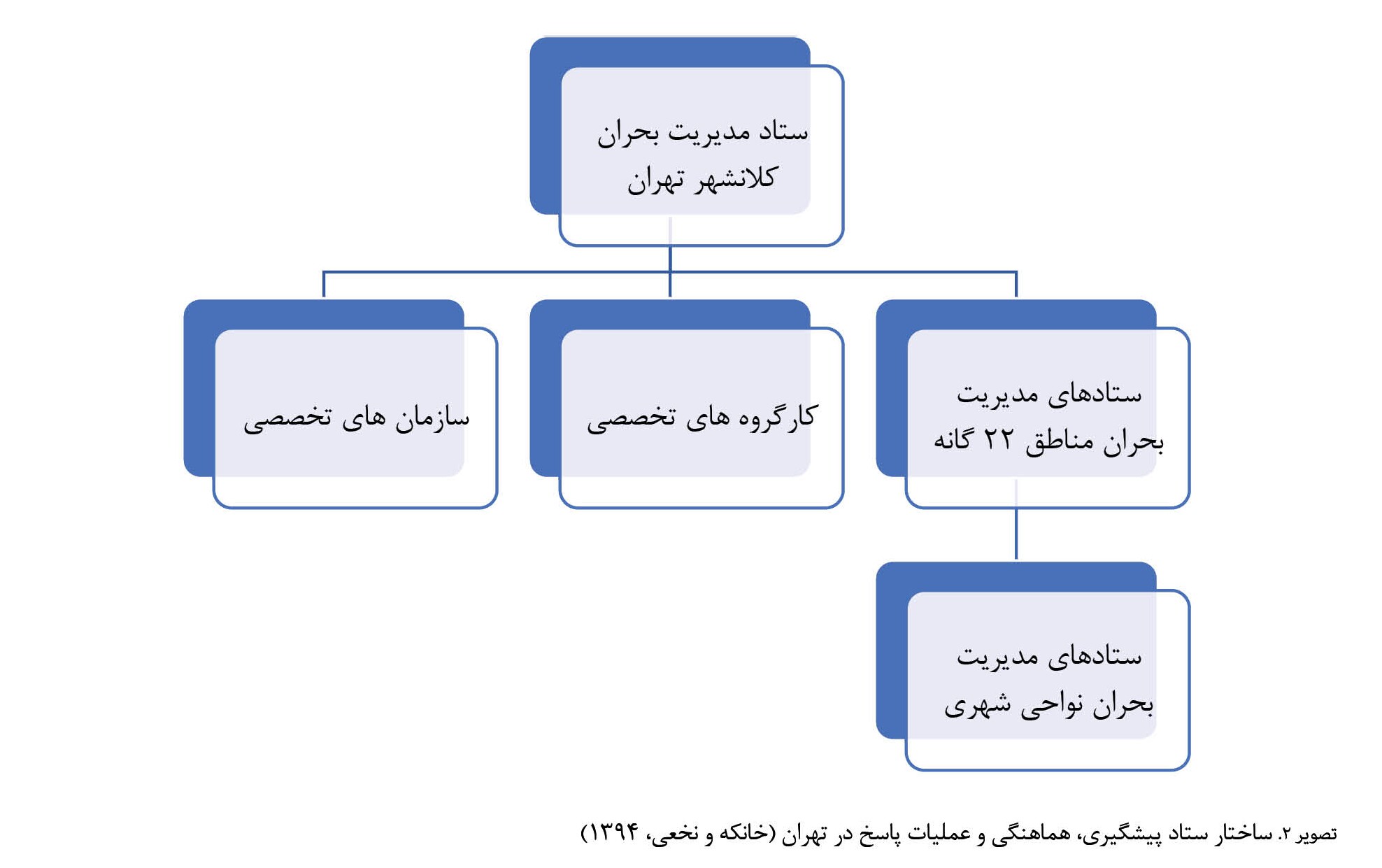
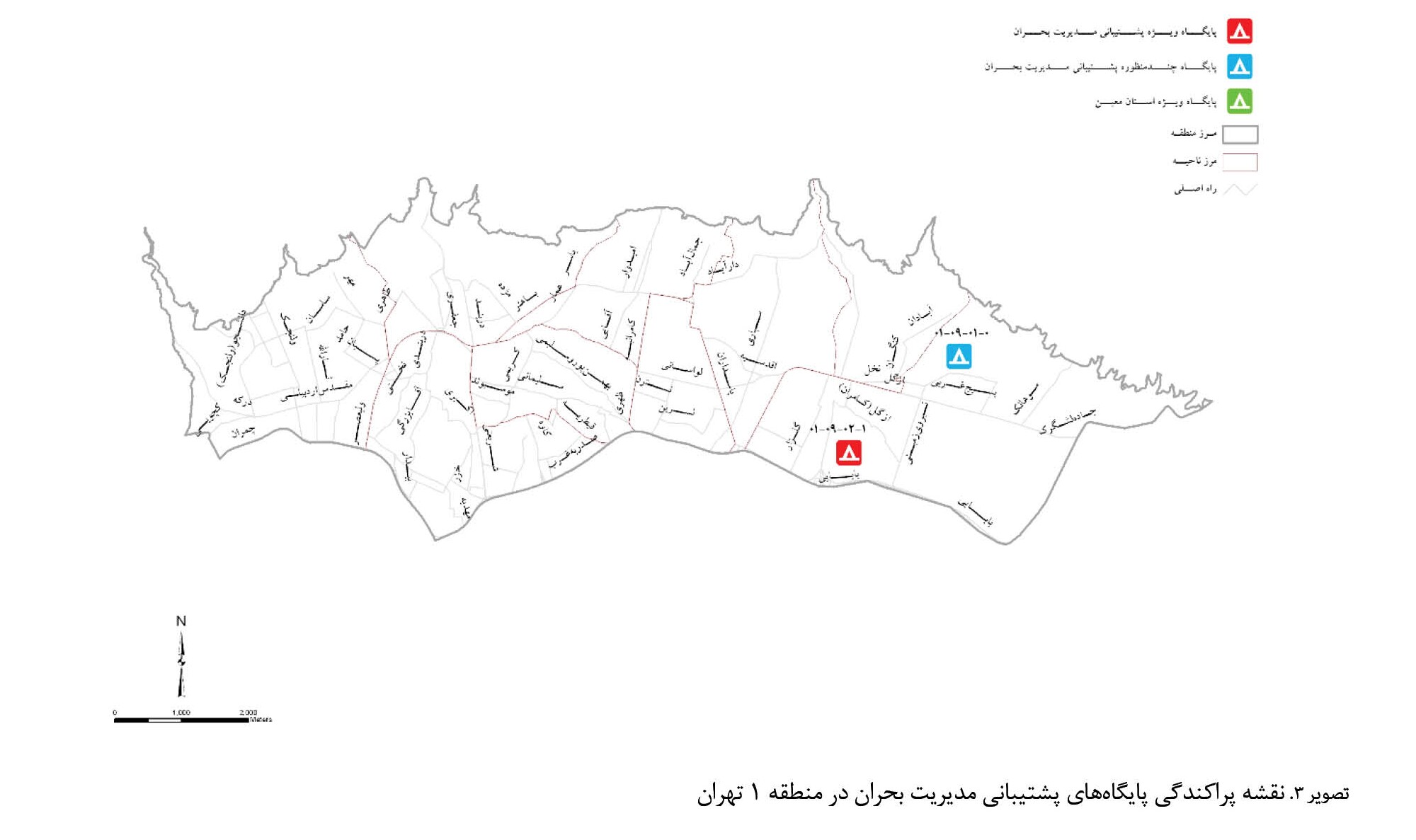
به استناد قانون مصوب مجلس شورای اسلامی، قانون مدیریت بحران کشور تحت لایحه مدیریت حوادث غیرمترقبه در کشور به تصویب رسیده است. براساس آن فرایند فعالسازی مرکز هدایت عملیات شهر تهران توسط سازمان پیشگیری و مدیریت بحران با هدف طراحی فرایند مدیریت اطلاعات در مرکز هدایت عملیات سازمان پیشگیری و مدیریت بحران شهر تهران انجام میپذیرد. زیرا، شهر تهران باتوجهبه نقشه پهنهبندی خطر نسبی زمینلرزه در ایران و وجود 4 گسل اصلی همچون گسل شمال تهران، مشأ و گسلهای شمال و جنوب شهر ری و وقوع زلزلههای مخرب تاریخی، در معرض وقوع زلزلههایی با قدرت بیش از 7 ریشتر است. علاوهبر زلزله مخاطرههای دیگری چون سیل، نشست زمین و غیره شهر تهران را تهدید میکنند. بنابراین توجه ویژه به مدیریت خطر در حوادث و بلایا و وجود مراکز هدایت عملیات در کلانشهر تهران بسیار ضروری است. برایناساس، منطقه 1 شهر تهران بهعنوان نمونه در نظر گرفته شده است. مطابق با
تصویر شماره 3 که نقشه پراکندگی پایگاههای پشتیبانی مدیریت بحران در این منطقه را نشان میدهد، یک پایگاه چندمنظوره پشتیبانی مدیریت بحران و یک پایگاه ویژه پشتیبانی مدیریت بحران در این منطقه در نظر گرفته شده است.
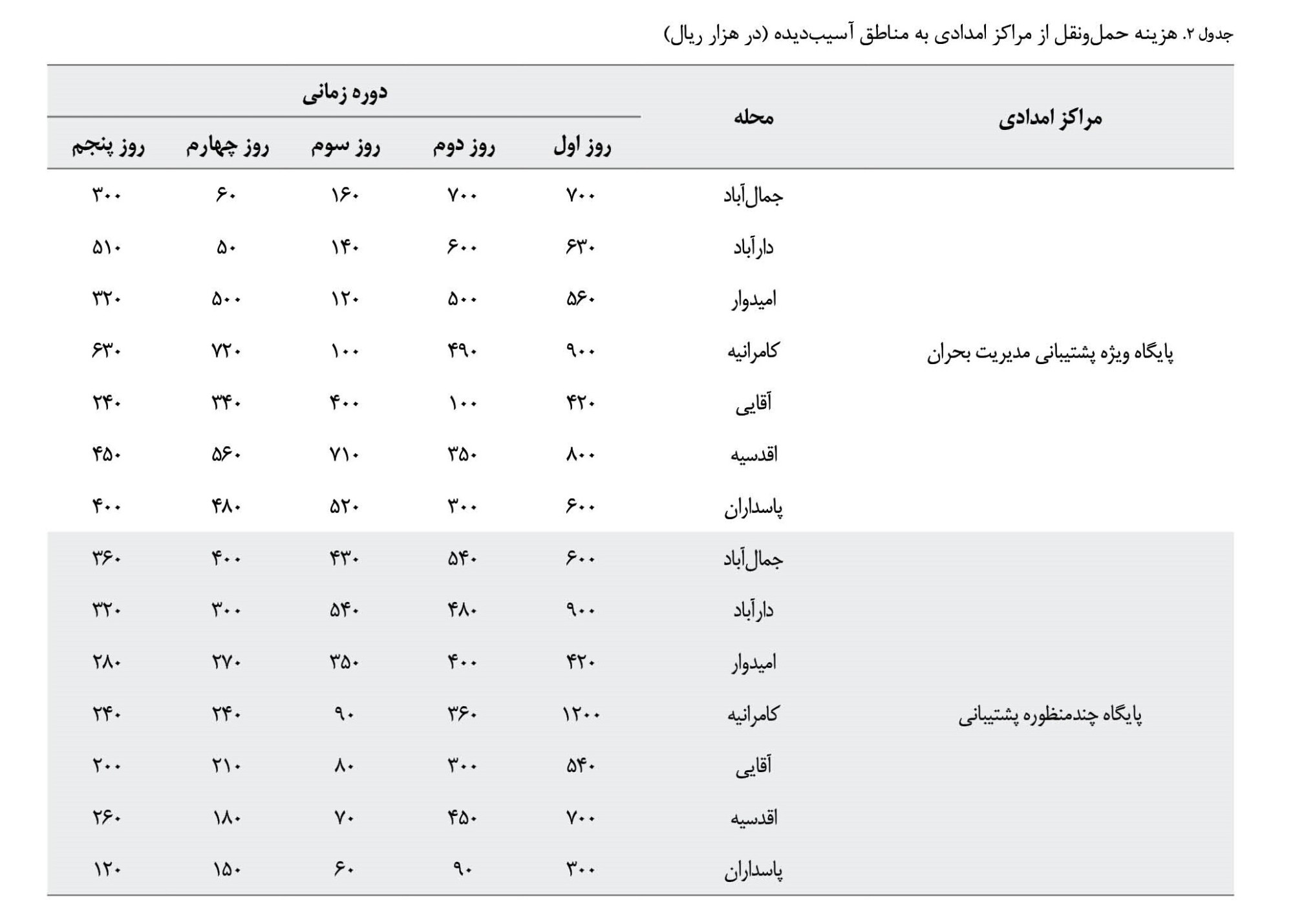
در این بخش، نتایج محاسباتی از مدل پیشنهادی نشان داده شده است. برای اجرای مدل از نرمافزار LINGO نسخه 18استفاده شده است. در این مقاله مسئله تخصیص کالای امدادی برای ۷ محله آسیبدیده در منطقه ۱ تهران انجام شده است. این ۷ محله توسط 2 پایگاه امدادی پشتیبانی میشوند و اقلام امدادی را دریافت میکنند. هزینه حملونقل و مواد قابلعرضه از هریک از مراکز نجات به مناطق آسیبدیده در
جدولهای شماره 2 و
3 نشان داده شده است.
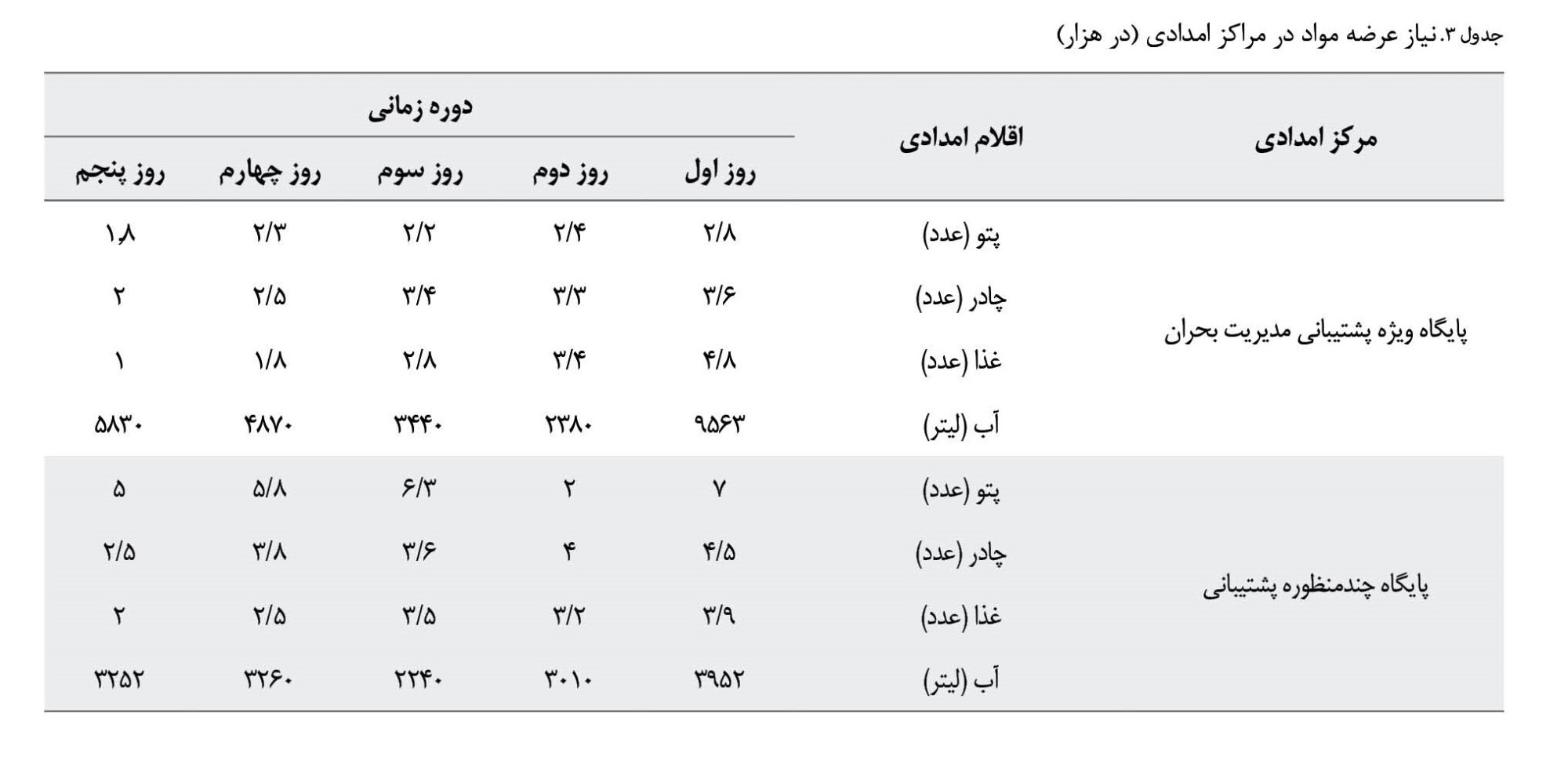
همچنین هزینه ثابت و متغیر از هر مرکز امدادرسانی به محلههای آسیبدیده در
جدول شماره 4 نشان داده شده است.

با اجرای مدل، مقدار بهینه متغیر تخصیص اقلام امدادی از مرکز امدادی به مناطق آسیبدیده مشخص میشود. براساس آن درمییابیم که هر ناحیه از کدام مرکز امدادی، اقلام ضروری را دریافت میکند. در
جدول شماره 5، مقدار متغیر vplt که تخصیص اقلام امدادی از مرکز امدادی p به منطقه آسیبدیده را مشخص میکند نشان داده شده است.
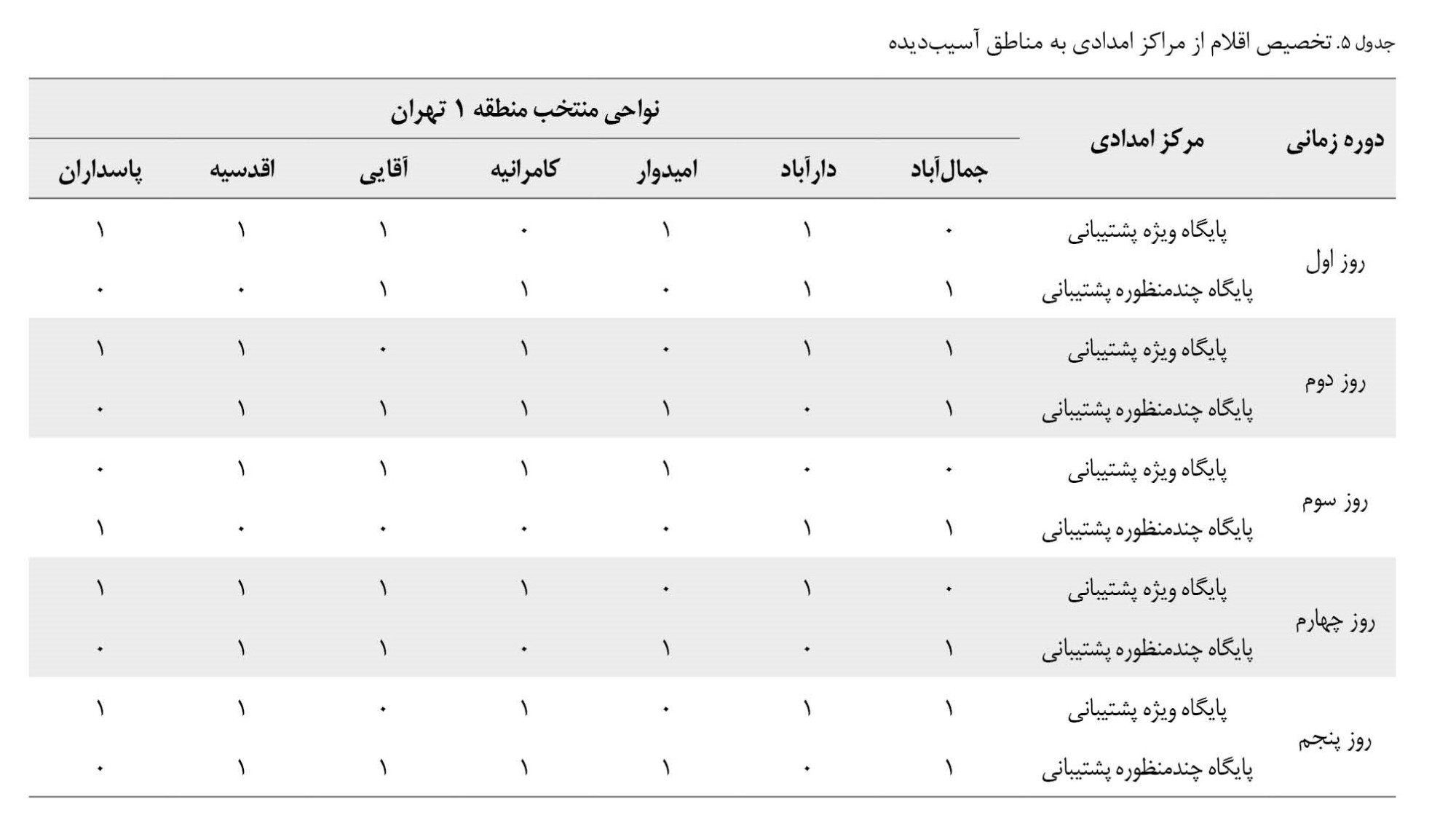
باتوجهبه ادبیات موجود، 4 نوع کالای ضروری در هنگام وقوع زلزله اعم از پتو، چادر، غذا و آب
دانشور و همکاران، 2023 و
وانگ و همکاران (2023) در نظر گرفته شده است. باتوجهبه
جدول شماره 6، تخصیص نحوه دریافت امدادرسانی به هریک از نواحی از مراکز امدادی مشخص شده است. همانطور که مشخص شده است همه نواحی اقلام امدادی را دریافت میکنند. برخی از نواحی از هر 2 مرکز امدادی اقلام ضروری را دریافت میکنند که به دلیل عدم برآورد تقاضا توسط یک پایگاه امدادی لازم است بخشی از تقاضا توسط پایگاه دیگر تأمین شود. در
جدول شماره 6، مشخص شده است که از هریک از مراکز امدادی چه اقلامی در هر دوره به مناطق ارسال میشود.
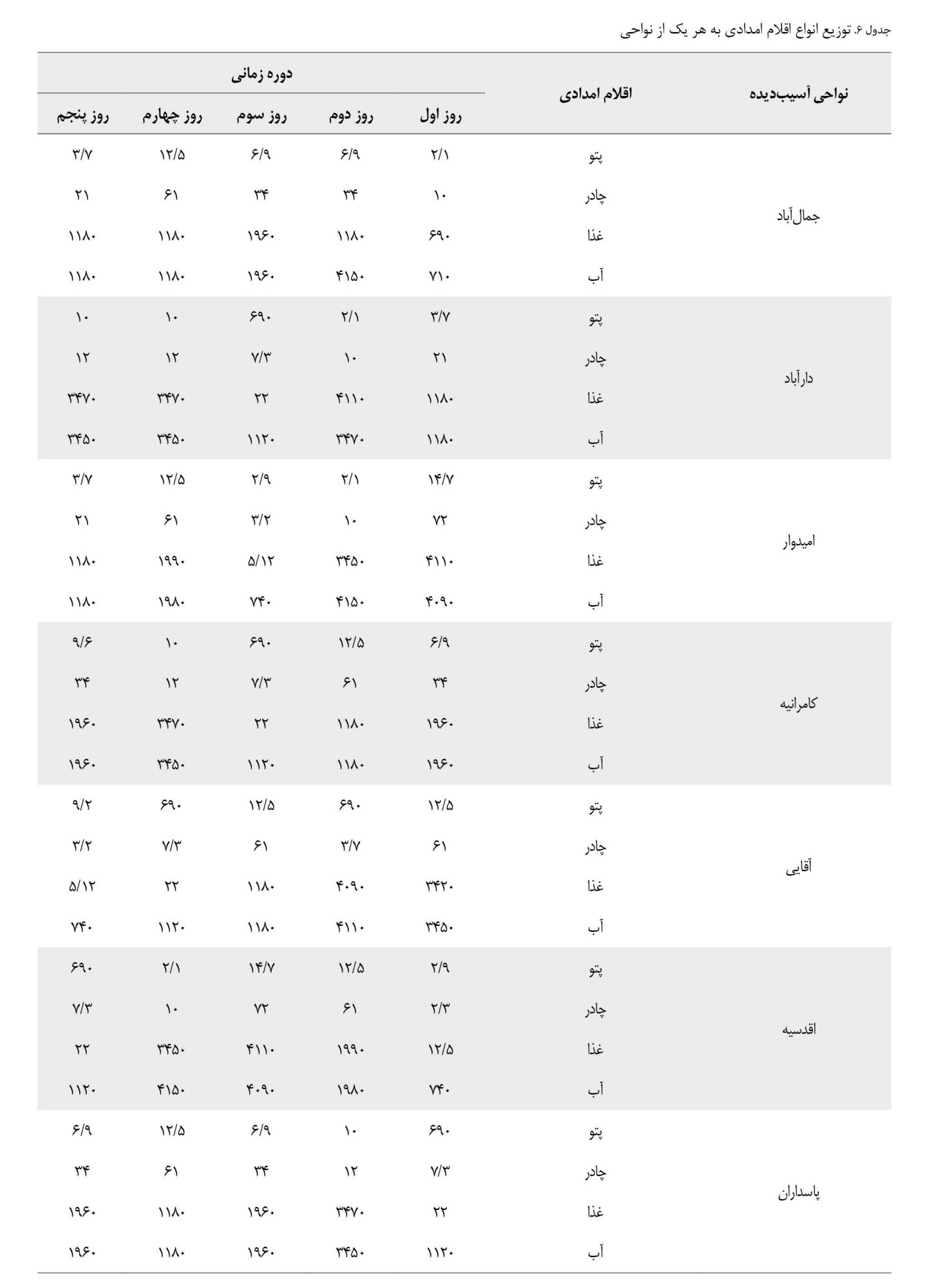
باتوجهبه اینکه مسئله چندهدفه در این مقاله، با استفاده از روش مجموع وزندارشده محاسبه شده است، مقدار بهینه تابع هدف وابسته به مقدار اوزانی است که برای توابع هدف در نظر میگیریم. ازآنجاییکه فرم تابع هدف در مسئله مجموع وزندارشده بهصورت w
1 f
1+w
2 f_
2+w
3 f
3 است و مجموع اوزان برابر با 1 است، حالتهای مختلفی برای ضرایب در نظر گرفته شود که در
جدول شماره 7 نشان داده شده است.
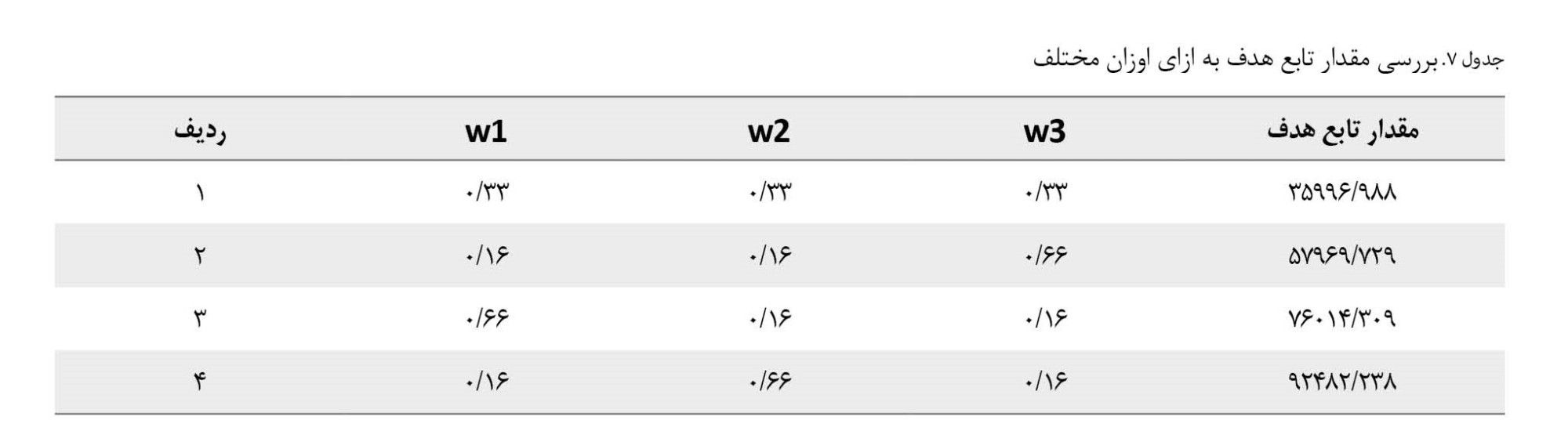
براساس نتایج بهدستآمده برای تابع هدف مشاهده میشود که مقدار تابع هدف بهشدت به اوزان توابع هدف وابسته است. برای مثال، هرچه وزن تابع هدف دوم کاهش پیدا میکند، مقدار تابع هدف ترکیبی افزایش مییابد و رابطه معکوس در مقدار تابع هدف ترکیبی ایجاد میکند.
تحلیل حساسیت
در این بخش تأثیر مقدار عرضه برای مواد ضروری q در مرکز امدادی p در هر دوره را بر روی مقدار تابع هدف میسنجیم و آن را با وضعیت موجود بررسی میکنیم. برای این منظور، مقدار پارامتر s
pqt را 10 درصد افزایش و کاهش میدهیم. همانطور که در
تصویر شماره 4 نشان داده شده است در صورت کاهش در مقدار پارامتر s
pqt مقدار تقاضای برآوردهنشده افزایش میباید و در همه دورهها اقلام ضروری با کمبود روبهرو میشوند.
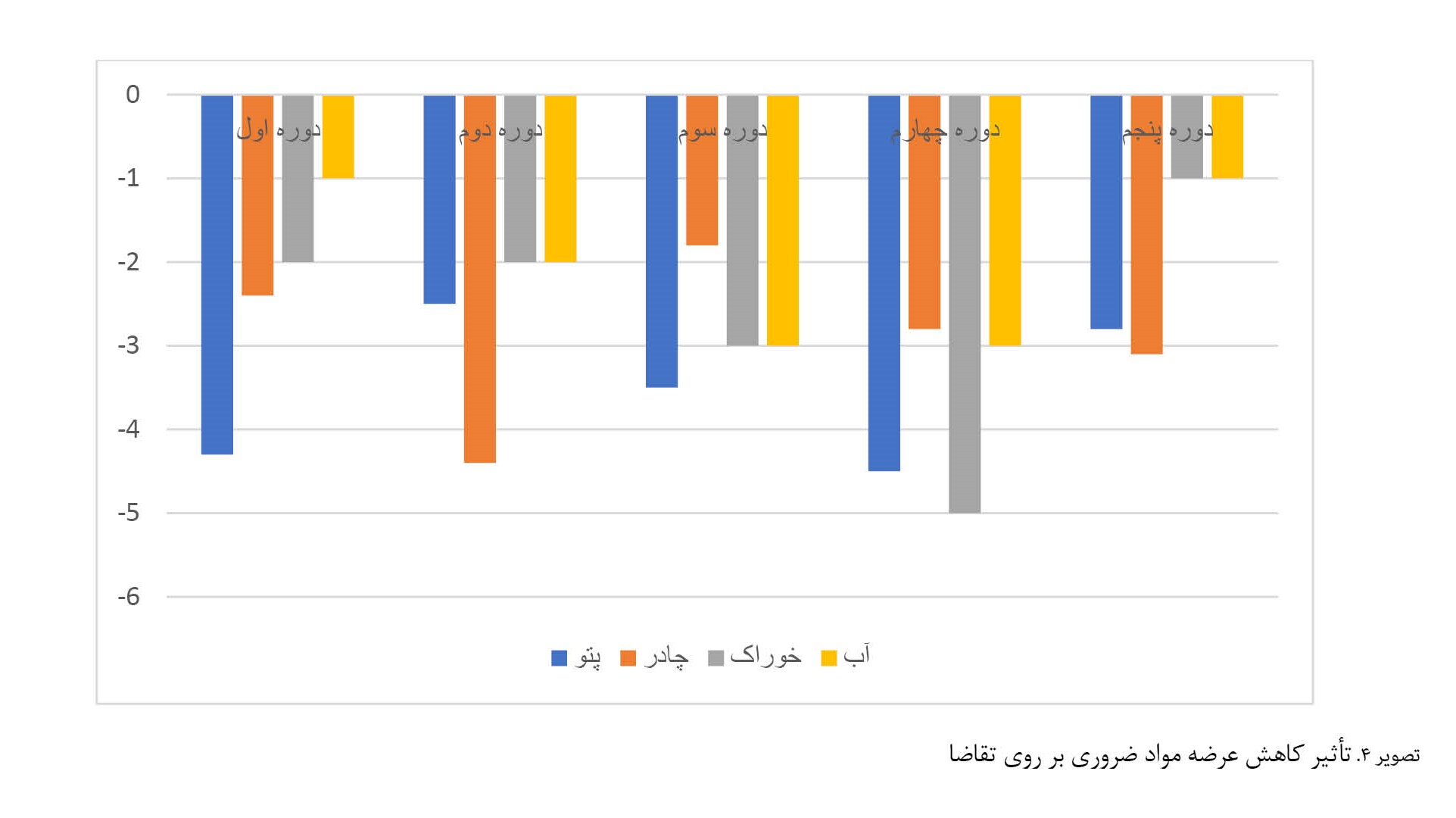
در
جدول شماره 8، میزان کمبود هریک از اقلام امدادی براساس هر دوره زمانی نشان داده شده است.
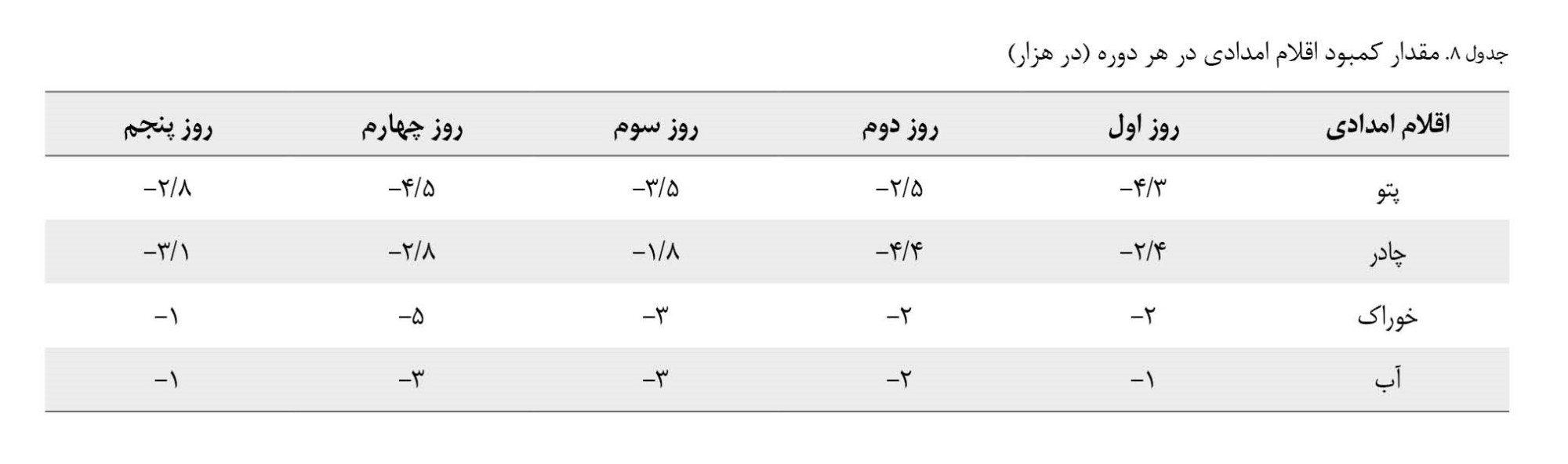
این کمبود بر روی مطلوبیت توزیع در میان تقاضاکنندگان تأثیر میگذارد. زیرا کاهش در مقدار عرضه باعث ایجاد عدم مطلوبیت در میان تقاضا کنندگان میشود و تأثیر سوء بر روی عملکرد زنجیره تأمین بشردوستانه و توزیع منصفانه میگذارد. زیرا در این صورت بسیاری از تقاضاها بدون پاسخ باقی میمانند.همچنین اگر مقدار پارامتر را افزایش دهیم، با مازاد اقلام روبهرو میشویم و باتوجهبه درنظرگرفتن پنجره زمانی، ممکن است تقاضا برای برخی از اقلام خوراکی وجود نداشته باشد و با فساد روبهرو شوند که دراینصورت نیز هزینه اضافه به زنجیره تحمیل میشود (
تصویر شماره 5).
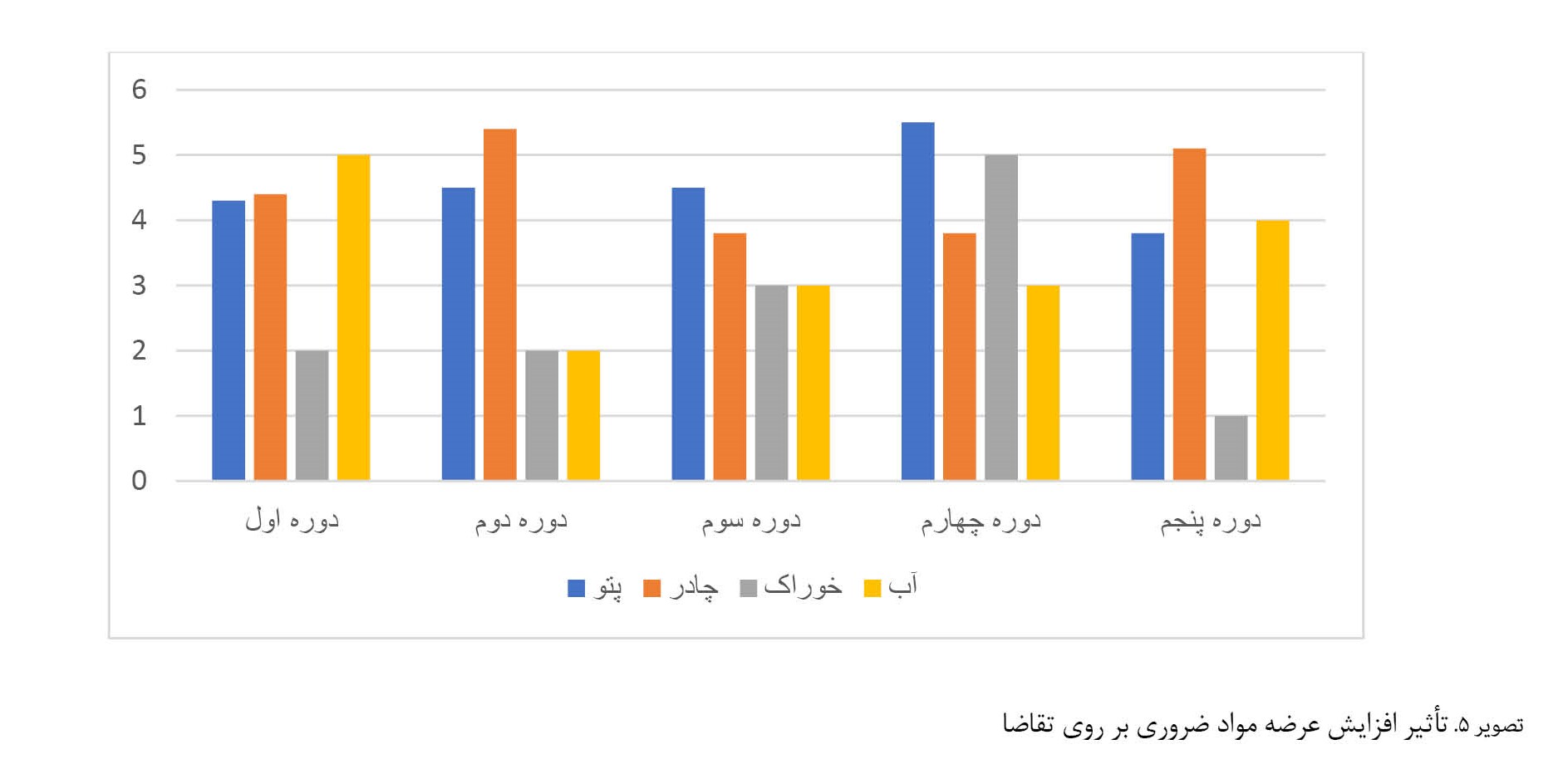
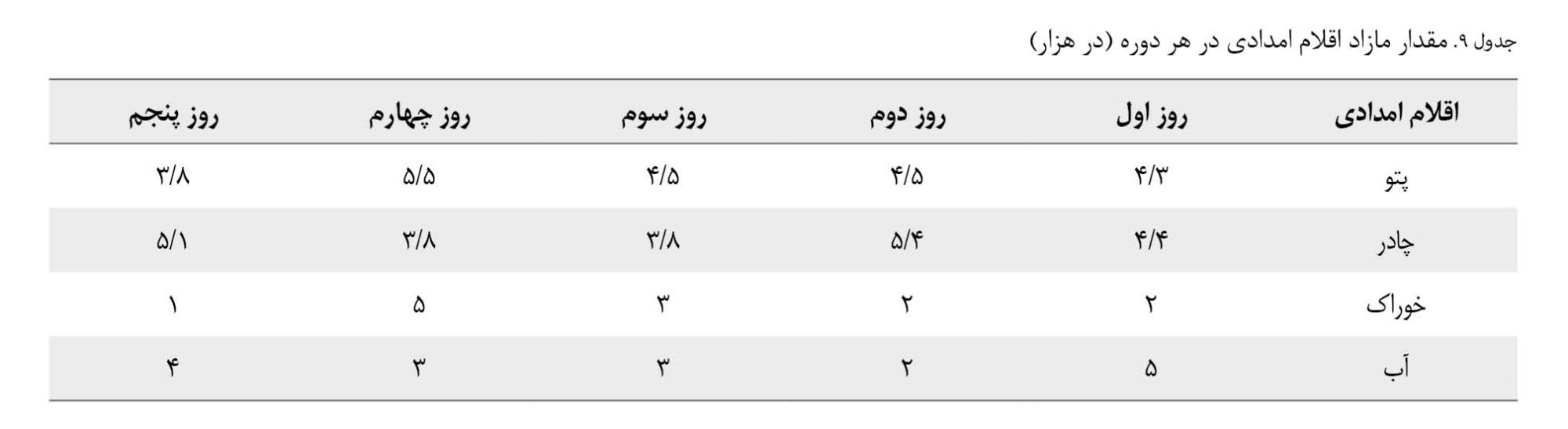
در
جدول شماره 9، میزان مازاد هریک از اقلام امدادی براساس هر دوره زمانی نشان داده شده است.
 بحث
بحث
در این مقاله یک مدل برنامهریزی ریاضی برای توزیع اقلام امدادرسانی در یک زنجیره تأمین بشردوستانه در 2 سطح بالا و پایین ارائه شده است. بنابراین، این مقاله در راستای تحقق اهداف ارائه یک مدل بهینهسازی برای توزیع بستههای معیشتی در زنجیره تأمین بشردوستانه برای مقابله با بحران است. برای این منظور، یک زنجیره تأمین بشردوستانه چندهدفه و چندسطحی جهت توزیع عادلانه بستههای معیشتی برای مقابله با بحران توسعه داده شده است. نظر به اینکه تحقیقات درمورد تخصیص مواد اضطراری معمولاً 1 تا 2 شاخص را در نظر میگیرند، این مقاله 3 بُعد شاخصهای لجستیک بشردوستانه را بررسی میکند که عبارتاند از: هزینه دسترسی، نرخ تقاضای برآوردهنشده در هر دوره و فاصله بین نرخ پر کردن تقاضا و نرخ رضایت ایدئال تقاضا در کل دوره. علاوهبراین، بهجای استفاده از شبکههای توزیع امدادرسانی یگانه ـ منطقه آسیبدیده منفرد یا حالتهای توزیع تکدورهای یا 2 دوره، این مقاله یک مدل تخصیص مواد ضروری اعم از خوراکی، آب، پتو و چادر از مراکز امدادرسانی چندگانه به مناطق آسیبدیده مختلف پیشنهاد میکند که قادر است رفتار منصفانه در توزیع اقلام در بین مناطق داشته باشد، زیرا در این حالت برنامهریزی برای مناطق آسیبدیده با وضعیت واقعی سازگارتر است. مدل پیشنهادشده در این مقاله برای سوانح طبیعی ناگهانی در مقیاس محلی مناسب است که در مناطق شهری (با تعداد معینی از جمعیت ساکن) رخ میدهد. طبق نتایج، در صورت کاهش در مقدار پارامتر مقدار عرضه اقلام امدادی مقدار تقاضای برآوردهنشده افزایش میباید و در همه دورهها اقلام ضروری با کمبود روبهرو میشوند. این کمبود بر روی مطلوبیت توزیع در میان تقاضاکنندگان تأثیر میگذارد. زیرا کاهش در مقدار عرضه باعث ایجاد عدم مطلوبیت در میان تقاضا کنندگان میشود و تأثیر سوء بر روی عملکرد زنجیره تأمین بشردوستانه و توزیع منصفانه میگذارد. در این صورت بسیاری از تقاضاها بدون پاسخ باقی میمانند. همچنین اگر مقدار عرضه اقلام امدادی افزایش دهیم، با مازاد اقلام روبهرو میشویم و باتوجهبه در نظر گرفتن پنجره زمانی ممکن است تقاضا برای برخی از اقلام خوراکی وجود نداشته باشد و با فساد روبهرو شوند که در اینصورت نیز هزینه اضافه به زنجیره تحمیل میشود. باتوجهبه اینکه تهران بهعنوان پایتخت ایران و یکی از شهرهای پرجمعیت، با مخاطرات زلزلهای قابلتوجهی روبهرو است پیشنهادات کاربردی این تحقیق به شرح زیر است:
• بررسی و تحلیل نیازهای اساسی مناطق آسیبدیده: با بررسی و تحلیل دقیق، نیازهای اساسی و اولیه مناطق آسیبدیده، ازجمله غذا، آب، پتو، چادر و غیره آغاز شود. این بررسی کمک میکند تا اقلام موردنیاز برای توزیع امداد بهموقع شناسایی شوند.
• تعیین مسیرهای ارسال امداد: با استفاده از مدل ریاضی پیشنهادشده می توان بهطور دقیق مشخص کرد که هریک از مناطق آسیبدیده از چه پایگاههای امدادیای باید امدادرسانی دریافت کنند.
• مدیریت موجودی امدادها: با استفاده از مدل پیشنهادشده، بهینهترین میزان موجودی امدادها برای هر منطقه آسیبدیده به ازای هر نوع محصول امدادی مشخص شده است. این شامل تعیین نوع و تعداد محصولات موردنیاز در هر منطقه و زمانبندی تحویل امدادها میشود.
نتیجهگیری
تحقیقات قبلی، مانند مطالعه
رضایی و همکاران (2021)،
کائو و همکاران (2021)،
ونگ و همکاران (2021) و
منصوری و همکاران (2020) که مربوط به تخصیص تدارکات اضطراری هستند دارای اهداف تک یا دوگانه بودهاند و بهندرت سه هدف را مانند این تحقیق در ابعاد مختلف انتخاب کردهاند. تعداد اهداف انتخابشده مهم نیست، مهم این است که توزیع منصفانه بهندرت در تمامی مقالات بهعنوان هدف در نظر گرفته شده است که در این تحقیق به آن توجه شده است. مطالعه 3 هدف زنجیره تأمین بشردوستانه در ابعاد مختلف، تصمیمگیرندگان را قادر میکند هنگام انتخاب استراتژی توزیع منابع اضطراری، بهینهسازی کلی را انجام دهند. مدل این مطالعه برخلاف مطالعات
میچ و کوینچو (2019)؛
هورنر و همکاران (2018)؛ و
کین و همکاران (2018) مدل تخصیص تدارکات اضطراری چنددورهای و چندگانه است. ازآنجاکه بلایای طبیعی ناگهانی در مقیاس بزرگ باعث ایجاد چندین منطقه فاجعه در یک زمان میشوند، یک مرکز نجات نمیتواند وضعیت واقعی را برآورد کند و هزینه نجات در این صورت افزایش مییابد. اکثر مطالعات کنونی مانند
دانشور و همکاران، 2023 و
وانگ و همکاران (2023) از شبکههای امدادی مراکز امداد و نجات واحد و مناطق چند بلایا استفاده کردهاند. اما این مطالعه با استفاده از شبکه تخصیص اضطراری مراکز امدادرسانی مختلف و مناطق آسیبدیده گوناگون درک واقعبینانهتری برای مواجهه با مسئله ایجاد کرده است. مهمترین محدودیت پژوهش حاضر در مواجهه با مدلسازی ریاضی رخ میدهد. در صورت افزایش ابعاد مسئله ممکن است روشهای حل مرسوم قادر به حل مدل ریاضی پیشنهادشده نباشند که مهمترین چالش پیشِروی محققین شمرده میشود. این مقاله پیشنهاد میکند تحقیقات آینده باید عوامل واقعیتر برای برخی پارامترها، مانند تقاضا و هزینههای ثابت و متغیر را در نظر بگیرند. برای این منظور، میتوان عدم قطعیت را ازطریق ایجاد یک برنامهریزی استوار وارد مدلسازی کرد.
ملاحظات اخلاقی
پیروی از اصول اخلاق پژوهش
نویسندگان این تحقیق بر خود لازم می دانند تا اعلام کنند به منظور رعایت اصل محرمانگی از کلیه اطلاعات نزد خود محافظت میکنند. همچنین، از نام بردن اشخاصی که اطلاعات مورد نیاز را در اختیارمان قرار دادند پرهیز به عمل آمده است.
حامی مالی
این مقاله از یک دکتری استخراج شده است. پایاننامه. این تحقیق هیچ کمک مالی خاصی از هیچ سازمان تأمین مالی در بخش های عمومی، تجاری یا غیرانتفاعی دریافت نکرده است.
مشارکت نویسندگان
نرم افزار: رضا نریمانی و حسین عموزاد خلیلی; بررسی و نگارش پیش نویس اصلی: رضا نریمانی; مفهومسازی، منابع، بررسی و ویرایش: مجید معتمدی; نقد و بررسی و تدوین: حسین عموزاد خلیلی.
تعارض منافع
بنابر اظهار نویسندگان این مقاله تعارض منافع ندارد.
References
Agarwal, S., Kant, R., Shankar, R. (2020). Evaluating solutions to overcome humanitarian supply chain management barriers: A hybrid fuzzy SWARA–Fuzzy WASPAS approach. International Journal of Disaster Risk Reduction, 51, 101838. [DOI:10.1016/j.ijdrr.2020.101838]
Aghajani, M., Torabi, S. A., & Heydari, J. (2020). A novel option contract integrated with supplier selection and inventory prepositioning for humanitarian relief supply chains. Socio-Economic Planning Sciences, 71, 100780. [DOI:10.1016/j.seps.2019.100780]
Anaya-Arenas, A. M., Ruiz, A., & Renaud, J. (2018). Importance of fairness in humanitarian relief distribution. Production Planning & Control, 29(14), 1145-1157. [DOI:10.1080/09537287.2018.1542157]
Behl, A., Dutta, P., & Gupta, S. (2019). Critical success factors for humanitarian supply chain management: a grey DEMATEL approach. IFAC-PapersOnLine, 52(13), 159-164. [DOI:10.1016/j.ifacol.2019.11.169]
Boonmee, C., Arimura, M., & Asada, T. (2017). Facility location optimization model for emergency humanitarian logistics. International Journal of Disaster Risk Reduction, 24, 485-498. [DOI:10.1016/j.ijdrr.2017.01.017]
Cao, C., Liu, Y., Tang, O., & Gao, X. (2021). A fuzzy bi-level optimization model for multi-period post-disaster relief distribution in sustainable humanitarian supply chains. International Journal of Production Economics, 235, 108081. [DOI:10.1016/j.ijpe.2021.108081]
Chobar, A. P., Adibi, M. A., & Kazemi, A. (2022). Multi-objective hub-spoke network design of perishable tourism products using combination machine learning and meta-heuristic algorithms. Environment, Development and Sustainability, 1-28. [DOI:10.1007/s10668-022-02350-2]
Daneshvar, M., Jena, S. D., & Rei, W. (2023). A two-stage stochastic post-disaster humanitarian supply chain network design problem. Computers & Industrial Engineering, 183, 109459. [DOI:10.1016/j.cie.2023.109459]
Dora, M., Kumar, M. (2022). Operational improvement programs and humanitarian operations. Production Planning & Control, 33(6-7), 513-6. [Link]
Gupta, U., & Ranganathan, N. (2006). Social fairness in multi-emergency resource management. Paper presened at: 2006 IEEE International Symposium on Technology and Society, Queens, NY, USA, 08-10 June 2006. [DOI:10.1109/ISTAS.2006.4375884]
Horner, M. W., Ozguven, E. E., Marcelin, J. M., & Kocatepe, A. (2018). Special needs hurricane shelters and the ageing population: development of a methodology and a case study application. Disasters, 42(1), 169-186. [DOI:10.1111/disa.12233] [PMID]
Jahangiri, S., Abolghasemian, M., Pourghader Chobar, A., Nadaffard, A., & Mottaghi, V. (2021). Ranking of key resources in the humanitarian supply chain in the emergency department of iranian hospital: a real case study in COVID-19 conditions. Journal of Applied Research on Industrial Engineering, 8(Special Issue), 1-10. [Link]
Jahangiri, Sh., Abolghasemian, M., Ghasemi, P., & Pourghader Chobar, A. (2023). Simulation-based optimization: Analysis of the emergency department resources under COVID-19 conditions. International Journal of Industrial and Systems Engineering, 43(1), 1-19. [DOI:10.1504/IJISE.2023.128399]
Jiang, P., Wang, Y., Liu, C., Hu, YC., Xie, J. (2020). Evaluating critical factors influencing the reliability of emergency logistics systems using multiple-attribute decision making. Symmetry, 12(7),1115. [Link]
Kanoun, I., Chabchoub, H., & Aouni, B. (2010). Goal programming model for fire and emergency service facilities site selection. INFOR: Information Systems and Operational Research, 48(3), 143-153. [DOI:10.3138/infor.48.3.143]
Ma, Y., Xu, W., Qin, L., Zhao, X., & Du, J. (2019). Hierarchical supplement location-allocation optimization for disaster supply warehouses in the Beijing-Tianjin-Hebei region of China. Geomatics, Natural Hazards and Risk, 10(1), 102-117. [DOI:10.1080/19475705.2018.1508077]
Maghfiroh, M. F., & Hanaoka, S. (2020). Multi-modal relief distribution model for disaster response operations. Progress in Disaster Science, 6, 100095. [DOI:10.1016/j.pdisas.2020.100095]
Maharjan, R., & Hanaoka, S. (2020). A credibility-based multi-objective temporary logistics hub location-allocation model for relief supply and distribution under uncertainty. Socio-Economic Planning Sciences, 70, 100727. [DOI:10.1016/j.seps.2019.07.003]
Mamashli, Z., Bozorgi-Amiri, A., Dadashpour, I., Nayeri, S., & Heydari, J. (2021). A heuristic-based multi-choice goal programming for the stochastic sustainable-resilient routing-allocation problem in relief logistics. Neural Computing and Applications, 33,14283–14309. [DOI:10.1007/s00521-021-06074-8]
Manopiniwes, W., & Irohara, T. (2014). A review of relief supply chain optimization. Industrial Engineering and Management Systems, 13(1), 1-14. [DOI:10.7232/iems.2014.13.1.001]
Mansoori, S., Bozorgi-Amiri, A., & Pishvaee, M. S. (2020). A robust multi-objective humanitarian relief chain network design for earthquake response, with evacuation assumption under uncertainties. Neural Computing and Applications, 32(7), 2183-2203. [DOI:10.1007/s00521-019-04193-x]
Mejia‐Argueta, C., Gaytan, J., Caballero, R., Molina, J., & Vitoriano, B. (2018). Multicriteria optimization approach to deploy humanitarian logistic operations integrally during floods. International Transactions in Operational Research, 25(3), 1053-1079. [DOI:10.1111/itor.12508]
Miç, P., Koyuncu, M., & Hallak, J. (2019). Primary health care center (PHCC) location-allocation with multi-objective modelling: A case study in Idleb, Syria. International Journal of Environmental Research and Public Health, 16(5), 811. [DOI:10.3390/ijerph16050811] [PMID]
Mirzapour Al-e-hashem, S. M. J., Amoozad Khalili, H., & Khazaei Kouhpar, R. (2022). [An ambulance routing problem in organ transplant supply chain considering traffic congestion (Persian)]. Journal of Industrial Management Perspective, 12(1), 261-291. [Link]
Mohammadi, S., Darestani, S. A., Vahdani, B., & Alinezhad, A. (2020). A robust neutrosophic fuzzy-based approach to integrate reliable facility location and routing decisions for disaster relief under fairness and aftershocks concerns. Computers & Industrial Engineering, 148, 106734. [DOI:10.1016/j.cie.2020.106734]
Nasr, A., Tavana, M., Alavi, B., & Mina, H. (2021). A novel fuzzy multi-objective circular supplier selection and order allocation model for sustainable closed-loop supply chains. Journal of Cleaner production, 287, 124994. [DOI:10.1016/j.jclepro.2020.124994]
Ozbay, E., Çavuş, Ö, & Kara, B. Y. (2019). Shelter site location under multi-hazard scenarios. Computers & Operations Research, 106, 102-118. [DOI:10.1016/j.cor.2019.02.008]
Patil, I., Zucchelli, MM., Kool, W., Campbell, S., Fornasier, F., Calò, M., Silani, G., Cikara, M., Cushman, F. (2021). Reasoning supports utilitarian resolutions to moral dilemmas across diverse measures. Journal of Personality and Social Psychology, 120(2), 443. [Link]
Peng, D., Ye, C., & Wan, M. (2022). A multi-objective improved novel discrete particle swarm optimization for emergency resource center location problem. Engineering Applications of Artificial Intelligence, 111, 104725. [DOI:10.1016/j.engappai.2022.104725]
Pirouz, B., & Khorram, E. (2016). A computational approach based on the ε-constraint method in multi-objective optimization problems. Advances and Applications in Statistics, 49(6), 453-83. [DOI:10.17654/AS049060453]
Poornaser, M., Amoozadkhalili, H., Momeni, E., Movahedi, M. M., & Motamedi, M. (2022). [Routing disaster relief vehicles in a humanitarian supply chain (Persian)]. Disaster Prevention and Management Knowledge , 12(2), 205-216. [Link]
Praneetpholkrang, P., & Huynh, V. N. (2020). Shelter site selection and allocation model for efficient response to humanitarian relief logistics. In: M. Freitag, H. D. Haasis, H. Kotzab, & J. Pannek (Eds.), Dynamics in logistics. LDIC 2020. Lecture notes in logistics. Cham: Springer. [DOI:10.1007/978-3-030-44783-0_30]
Qin, W., Zhao, X., Ma, Y., Li, Y., Qin, L., & Wang, Y., et al. (2018). A multi-objective optimization based method for evaluating earthquake shelter location-allocation. Geomatics, Natural Hazards and Risk, 9(1), 662-677. [DOI:10.1080/19475705.2018.1470114]
Rajak, S., Mathiyazhagan, K., Agarwal, V., Sivakumar, K., Kumar, V., Appolloni, A. (2022). Issues and analysis of critical success factors for the sustainable initiatives in the supply chain during COVID-19 pandemic outbreak in India: A case study. Research in Transportation Economics, 93, 101114. [DOI:10.1016/j.retrec.2021.101114]
Rezaei Kallaj, M., Abolghasemian, M., Moradi Pirbalouti, S., Sabk Ara, M., & Pourghader Chobar, A. (2021). Vehicle routing problem in relief supply under a crisis condition considering blood types. Mathematical Problems in Engineering, 1-10. [DOI:10.1155/2021/7217182]
Roh, S. Y., Jang, H. M., & Han, C. H. (2013). Warehouse location decision factors in humanitarian relief logistics. The Asian Journal of Shipping and Logistics, 29(1), 103-120. [DOI:10.1016/j.ajsl.2013.05.006]
Roh, S. Y., Shin, Y. R., & Seo, Y. J. (2018). The Pre-positioned warehouse location selection for international humanitarian relief logistics. The Asian Journal of Shipping and Logistics, 34(4), 297-307. [DOI:10.1016/j.ajsl.2018.12.003]
Sabouhi, F., Bozorgi-Amiri, A., & Vaez, P. (2020). Stochastic optimization for transportation planning in disaster relief under disruption and uncertainty. Kybernetes, 50(9), 2632-2650. [DOI:10.1108/K-10-2020-0632]
Shao-hong, Y., Jia-Yang, N., Tai-long, C., Qiu-Tong, L., Cen, Y., & Jia-qing, C., et al. (2022). Location algorithm of transfer stations based on density peak and outlier detection. Applied Intelligence, 52, 13520–13532. [DOI:10.1007/s10489-022-03206-y]
Wang, B. C., Qian, Q. Y., Gao, J. J., Tan, Z. Y., & Zhou, Y. (2021). The optimization of warehouse location and resources distribution for emergency rescue under uncertainty. Advanced Engineering Informatics, 48, 101278. [DOI:10.1016/j.aei.2021.101278]
Wang, Z., Liu, Y., & Li, W. (2023). A globalized robust optimization method for sustainable humanitarian relief network design with uncertain scenario probabilities. Sustainable Cities and Society, 97, 104729. [DOI:10.1016/j.scs.2023.104729]
Wu, G. H., Chang, C. K., & Hsu, L. M. (2018). Comparisons of interactive fuzzy programming approaches for closed-loop supply chain network design under uncertainty. Computers & Industrial Engineering, 125, 500-513. [DOI:10.1016/j.cie.2018.09.022]
Yofrido, F. M., & Harjana, L. T. (2019). Social-fairness perception in natural disaster, learn from Lombok: a phenomenological report. Indonesian Journal of Anesthesiology and Reanimation, 1(1), 1-7. [DOI:10.20473/ijar.V1I12019.1-7]
Zheng, Y. J., Chen, S. Y., & Ling, H. F. (2015). Evolutionary optimization for disaster relief operations: A survey. Applied Soft Computing, 27, 553-566. DOI:10.1016/j.asoc.2014.09.041]