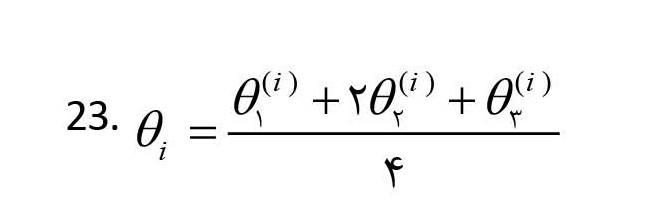مقدمه
در قرن بیستویکم، جهان شاهد بحرانهای طبیعی متعددی بوده است. طوفان عظیم کاترینا، سونامی آسیای جنوب شرقی و زلزله هائیتی ازجمله مهمترین آنهاست که آسیبها و تلفات جانی و مالی فراوانی را به همراه داشتهاند. در سالهای اخیر نیز پاندمی کووید ـ 19 تاکنون به مرگ بیش از 6/5 میلیون نفر منجر شده است که آمار قابلتوجهی است (
پایگاه داده بینالمللی سوانح، 2023). همه این سوانح این حقیقت را به جهانیان گوشزد میکنند که پیشبینیها و چارهاندیشیها و راههای مقابله و سازش با این سوانح بهمنظور کاهش تلفات جانی از اهمیت بالایی برخوردار هستند. تخصیص بهینه منابع و مکانیابی درست مراکز درمانی، از موضوعاتی هستند که مدیران و تصمیمگیرندگان میتوانند روی آن تمرکز کرده و عملکرد خود را دررابطهبا خدمترسانی به آسیبدیدگان بهبود بخشند.
به علت تعداد زیاد مجروحین و آسیبدیدگان پس از سوانح، در اغلب بیمارستانها و مراکز درمانی ظرفیت کافی برای خدمتدهی به آنها وجود ندارد. علاوهبراین، دررابطهبا سوانحی مثل سیل و زلزله، اکثر بیمارستانها و مراکز درمانی که در نزدیکی مناطق آسیبدیده هستند، تخریبشده و استفاده از آنها غیرممکن میشود. بنابراین استقرار تسهیلات بهداشتی و درمانی متحرک که تحت عنوان بیمارستانهای صحرایی شناخته میشوند، میتواند تا حدودی مشکل کمبود ظرفیت و عدم توانایی خدمات پزشکی محلی را برطرف کند، اما باید به این نکته توجه داشت که بیمارستانهای صحرایی در صورتی مفید خواهند بود که در همان روزهای اولیه پس از وقوع سانحه در محل استقرار یابند تا بتوانند از تلفات زیاد جلوگیری کنند و عملیات امدادرسانی سریعتر و با کیفیت بهتری انجام شود (
اختریاقدم و نوریزاده، 1385). نکته مهم دیگری که در احداث بیمارستانهای صحرایی باید توجه داشت، دررابطهبا محل استقرار بیمارستانهای صحرایی است. درواقع، اگر این تسهیلات درمانی در فاصله خیلی دوری نسبت به نواحی آسیبدیده احداث شوند، مدتزمان انتقال مجروحان از نواحی آسیبدیده به این تسهیلات زیاد میشود که همین عامل به افزایش تلفات جانی منجر میشود. بنابراین یکی از موضوعاتی که این پژوهش به آن میپردازد، تعیین محل مناسب بیمارستانهای صحرایی است.
موضوع دیگری که پس از سوانح طبیعی بسیار مهم و حیاتی است، استفاده صحیح از منابع محدود است. یکی از اولین اقدامات حیاتی بعد از سوانح، امدادرسانی به مصدومان و انتقال آنها به مراکز درمانی با وسایل نقلیه امدادی نظیر آمبولانس است. بنابراین نحوه تخصیص وسایل نقلیه امدادی به نواحی آسیبدیده بسیار مهم است. منبع دیگری که باید به آن توجه داشت، بودجه لازم برای احداث بیمارستانهای صحرایی است. درواقع، استقرار هر بیمارستان صحرایی هزینههایی را برای سازمانها به بار میآورد. بنابراین سازمانها باید از بودجه محدودی که در دست دارند، به بهترین شکل ممکن استفاده کنند. از دیگر منابع پزشکی مهم میتوان به داروهای پزشکی، تخت و پرسنل پزشکی (پزشکان و پرستاران) اشاره کرد که این منابع باید به هر بیمارستان صحرایی که استقرار مییابد، به شیوه مناسب تخصیص یابد. این پژوهش، تمام این منابع را دربر میگیرد و بر روی چگونگی استفاده از آنها تمرکز میکند.
سؤالات اصلی این پژوهش را میتوان بهصورت زیر بیان کرد:
• به چه تعداد بیمارستان صحرایی در شهر آمل نیاز است و این بیمارستانهای صحرایی در چه مکانهایی باید احداث شوند؟
• سایر سؤالات این پژوهش را میتوان بهصورت زیر بیان کرد:
• از منابع موجود چگونه استفاده شود تا به افراد بیشتری بتوان خدمترسانی کرد؟
• تأثیر مقدار بودجه بر کیفیت خدمترسانی به مصدومان چگونه خواهد بود؟
بخش پیشینه پژوهش، به مرور ادبیات مسائل مکانیابی بیمارستانهای صحرایی و تخصیص منابع پزشکی اختصاص دارد. در بخش روش تحقیق، درمورد روش انجام پژوهش بحث میشود. در بخش شرح مسئله، مسئله موردبحث در این پژوهش همراه با مفروضات آن، بهصورت دقیق شرح داده و یک مدل برنامهریزی عدد صحیح برای آن ارائه میشود. در بخش مطالعه موردی، مدل پیشنهادی به کمک دادههای مربوط به شهر آمل مورد ارزیابی قرار میگیرد و جواب بهینه مسئله و بینشهای مدیریتی در بخش یافتهها ارائه میشود. در آخر، نتایج کلی پژوهش و پیشنهادات برای مطالعات آینده در بخش نتیجهگیری آورده شده است.
پیشینه پژوهش
مطالعات نسبتاً زیادی درزمینه مکانیابی مراکز درمانی و تخصیص منابع در هنگام بحرانها انجام شده است.
لئو و لیانگ (2013) یک مدل برنامهریزی خطی پویا و 3 سطحی برای تخصیص منابع پزشکی که مبتنی بر مدلهای انتشار اپیدمی است، ارائه کردهاند. هدف این تحقیق، به حداقل رساندن هزینههای حملونقل منابع پزشکی در 3 سطح مختلف است. آنها برای حل این مسئله، یک الگوریتم ابتکاری پیشنهاد دادهاند. ز
هیری و همکاران (2014) بهمنظور افزایش کارایی شبکه زنجیره تأمین پیوند اعضا، یک مدل برنامهریزی احتمالی استوار برای مسئله مکانیابیتخصیص چنددورهای ارائه دادند. هدف این مطالعه به حداقل رساندن مجموع هزینههاست که شامل هزینههای استقرار مراکز درمانی، هزینههای مربوط به حملونقل و هزینههای مربوط به تقاضاهای برآوردهنشده میباشد.
کو و همکاران (2016) به تخصیص و طراحی ظرفیت مراکز فوریتهای پزشکی در یک منطقه معین پرداختند. مرکز درمانی انتخابشده در ازای ارائه خدمات پزشکی، مقدار مشخصی یارانه از دولت دریافت میکند. در این مطالعه، یک رویکرد برنامهریزی عدد صحیح برای به حداقل رساندن کل مبلغ یارانههای پرداختشده توسط دولت ارائه شده است.
سان و همکاران (2014) بر تخصیص بیماران و منابع بیمارستانها در یک شبکه مراقبتهای بهداشتی تمرکز میکنند. مدلهای ریاضی ارائهشده در این مطالعه بهمنظور بهینهسازی تخصیص بیماران است که روی کمینه کردن مسافت پیمودهشده بیماران تا بیمارستانها تمرکز میکنند. در مطالعه
کسایی و کلتون (2013) بودجه ثابتی باید به تسهیلات بهداشتی تخصیص پیدا کند. آنها یک رویکرد شبیهسازیبهینهسازی برای این مسئله ارائه دادند.
رامیرز و همکاران (2021) مکانیابی مراکز خدماتیدرمانی و تخصیص نیروی انسانی به آن مراکز را با هدف به حداقل رساندن زمان خدمترسانی به افراد، در منطقه آسیبدیده مورد بررسی قرار دادند. همچنین یک الگوریتم ابتکاری برای حل مسئله با مقیاس بزرگ پیشنهاد کردهاند.
آپته و همکاران (2015) با یک مدل برنامهریزی خطی به مکانیابی نقاط جمعآوری مصدومان با هدف بیشینهسازی توان عملیاتی در مواجهه با مصدومان میپردازند. در تحقیق آنها سعی میشود میزان استفاده از پرسنل، واحدهای ضدعفونی و آمبولانسها تعیین شود و مقدار کمبودها مشخص شود.
لی، اسمالی و همکاران (2009) به تعیین تعداد مراکز توزیع موردنیاز میپردازند. مدلهای ارائهشده در این تحقیق، تراکم جمعیت، حداکثر مسافتی که افراد باید طی کنند، انواع تسهیلات خصوصی و عمومی موجود و پرسنل در دسترس برای مراکز توزیع را در نظر گرفته شده و از رویکرد شبیهسازی در مقیاس بزرگ استفاده شده است.
زاریک و براندو (2002) مدلی را برای تخصیص منابع برای کنترل همهگیری مدلسازی کرده و از الگوریتمهای ابتکاری برای حل مسئله استفاده کردهاند. ضمناً آنها با استفاده از تجزیهوتحلیل دادهها، نشان دادهاند تخصیص منابع در طول افق زمانی مسئله، به جای تخصیص منابع در ابتدای افق زمانی، میتواند مزایای زیادی را به همراه داشته باشد.
اویانگ و همکاران (2020)، از مدلسازی و تجزیهوتحلیل ریاضی برای تخصیص تخت در بخش مراقبتهای ویژه بیمارستان در دورههایی که تقاضای بیماران زیاد است، استفاده کرده و یک مدل ریاضی پیچیده که در آن شرایط سلامتی بیماران باتوجهبه زنجیره مارکوف در طول زمان تغییر میکند، ارائه دادند. در این تحقیق با هدف به حداقل رساندن متوسط میزان مرگومیر در بلندمدت، سیاستهای بهینه تحت شرایط خاص ارائه شده است.
کویانس و ارول (2010)، یک مدل برنامهریزی ریاضی چند هدفه برای تخصیص بهینه منابع در هنگام همهگیری آنفولانزا ارائه کردهاند. منابع موردنظر آنها شامل بودجه برای واکسیناسیون، تختهای بخش مراقبتهای ویژه، دستگاههای تنفسی و تختهای بخش مراقبتهای غیرویژه است. این مدل ریاضی دارای 3 هدف، شامل به حداقل رساندن تعداد مرگومیر، تعداد موارد مبتلا و مجموع روزهای بیماری در طول اپیدمی آنفولانزا است.
آپورنک (2021) به تخصیص نیروی انسانی در بخش اورژانس بیمارستان در طول همهگیری کرونا پرداخته است. او یک مدل برنامهریزی ریاضی با هدف به حداقل رساندن تعداد پرستاران موردنیاز در شیفتهای مختلف ارائه کرد.
آنپاراسان و لژون (2019)، به مکانیابی مراکز درمانی در هنگام شیوع اپیدمی و همچنین تخصیص منابع پزشکی، مانند پرسنل پزشکی، آمبولانسها، داروی پزشکی و تختها پرداختند. آنها یک رویکرد برنامهریزی عدد صحیح با هدف بیشینهسازی خدمترسانی به بیماران، پیشنهاد داده و با دادههای مربوط به شیوع وبا در کشور هائیتی در سال 2010 آن را ارزیابی کردند.
در پژوهش حاضر که توسعهای از مقاله
آنپاراسان و لژون (2019) است، علاوه بر محدودیت منابعی که آنها در نظر گرفتند، محدودیتی برای زمان اتمام امدادرسانی در نظر گرفته شده است و وسایل نقلیه امدادی تا زمان مشخصی فرصت دارند تا به مصدومان خدمترسانی کنند. همچنین توسعه دیگری که صورت گرفته است، مربوط به بیمارستانهای فعال در اطراف نواحی آسیبدیده (بیمارستانهایی که در اثر سانحه تخریب نشدهاند و ظرفیت پذیرش آسیبدیدگان را دارند) است که در مدل لحاظ شده است و آسیبدیدگان میتوانند علاوه بر بیمارستانهای صحرایی احداثشده، به بیمارستانهای فعال در اطراف نواحی آسیبدیده نیز منتقل شوند. در
جدول شماره 1 مطالعات انجامشده درزمینه مکانیابی مراکز درمانی و تخصیص منابع بهصورت خلاصه آورده شده است.
 روش
روش
در این پژوهش به مدلسازی ریاضی مسئله مکانیابی مراکز درمانی موقت و تخصیص منابع بعد از زلزله پرداخته شده و برای ارزیابی مدل پیشنهادی، از دادههای واقعی شهر آمل واقع در استان مازندران استفاده شد. روش حل مدل پیشنهادی نیز یک روش دقیق محسوب میشود که جواب بهینه را با استفاده از نرمافزار بهینهسازی گمز به دست میآورد. در بخش بعدی به شرح دقیق مسئله و مدل ریاضی پیشنهادی پرداخته میشود.
شرح مسئله
کمبود بیمارستان و پرسنل پزشکی در نواحی آسیبدیده، در اغلب سوانح طبیعی و انسانساخت همچون زلزله، سیل و جنگ احساس میشود. همچنین تخلیه آسیبدیدگان و رساندن آنها به بیمارستان زمانبر خواهد بود. درحالیکه برخی از افراد آسیبدیده، نیازمند دریافت خدمات درمانی در اولین ساعات سانحه هستند. بنابراین احداث بیمارستانهای صحرایی در محلهای مناسب در هنگام بحران از اهمیت ویژهای برخوردار است.
مسئلهای که در این تحقیق، به بررسی و مدلسازی آن پرداخته شده است، یک مسئله مکانیابیتخصیص پس از وقوع بحران است. در این پژوهش، یک مدل برنامهریزی عدد صحیح بهمنظور تعیین مکانهای مناسب برای احداث بیمارستانهای صحرایی از بین مکانهای منتخب ارائه شده است. همچنین در این مدل، مسئله تخصیص بهینه آسیبدیدگان به بیمارستانهای فعال دارای ظرفیت پذیرش آسیبدیدگان در اطراف نواحی آسیبدیده نیز مطرح میشود. همچنین تعداد محدودی پرسنل پزشکی (پرستاران و پزشکان) در دسترس هستند که باید به بیمارستانهای صحرایی تخصیص یابند. بهطورکلی این تحقیق، بر روی استفاده بهینه از منابع موجود و محدودی، مثل بودجه، تختهای بیمارستانها، داروهای پزشکی، پرسنل پزشکی و آمبولانسها تمرکز میکند تا به بهبود در عملکرد و تصمیمگیری سازمانها منجر شود.
مفروضات اصلی در نظر گرفتهشده برای مدل ریاضی توسعه دادهشده در این مقاله بهصورت زیر هستند:
• منطقه آسیبدیده به نواحی کوچکتری تقسیم میشود و تعداد آسیبدیدگان هر ناحیه که باید به بیمارستان منتقل شوند، با جمعیت و شدت تخریب آن ناحیه برآورد میشود. شدت تخریب هر ناحیه آسیبدیده به دلیل ماهیت غیرقطعی آن، بهصورت یک عدد فازی در مدل در نظر گرفته شده است.
• 2 نوع بیمارستان در مدل لحاظ شده است: نوع اول بیمارستانهای فعال در اطراف نواحی آسیبدیده هستند که ظرفیت و توانایی پذیرش آسیبدیدگان را دارند. نوع دوم بیمارستانهای صحرایی هستند که میبایست با در نظر گرفتن بودجه محدودی که در دسترس است، در مکانهای منتخب احداث شوند.
سایر مفروضات مسئله بهصورت زیر هستند:
• درصدی از تختهای بیمارستانهای صحرایی برای بیماران خدمات اورژانس و یا آسیبدیدگان انتقالی به بیمارستان با وسیلهای به غیر از آمبولانس (فرضاً با وسیله شخصی) اختصاص داده میشود.
• ظرفیت آمبولانسها برای انتقال آسیبدیدگان به بیمارستانها با هم متفاوت است.
• افق برنامهریزی برای انتقال آسیبدیدگان به بیمارستانها با آمبولانس، محدود فرض شده است (این زمان برای بحرانهایی همانند زلزله معمولاً 72 ساعت در نظر گرفته میشود).
• هر آمبولانس در طول افق برنامهریزی حداکثر به یک ناحیه آسیبدیده میتواند تخصیص داده شود.
• انتقال آسیبدیدگان یک ناحیه با آمبولانس، فقط به بیمارستانهایی مجاز است که فاصله زمانی بین آنها بیشتر از فاصله مجاز زمانی نباشد.
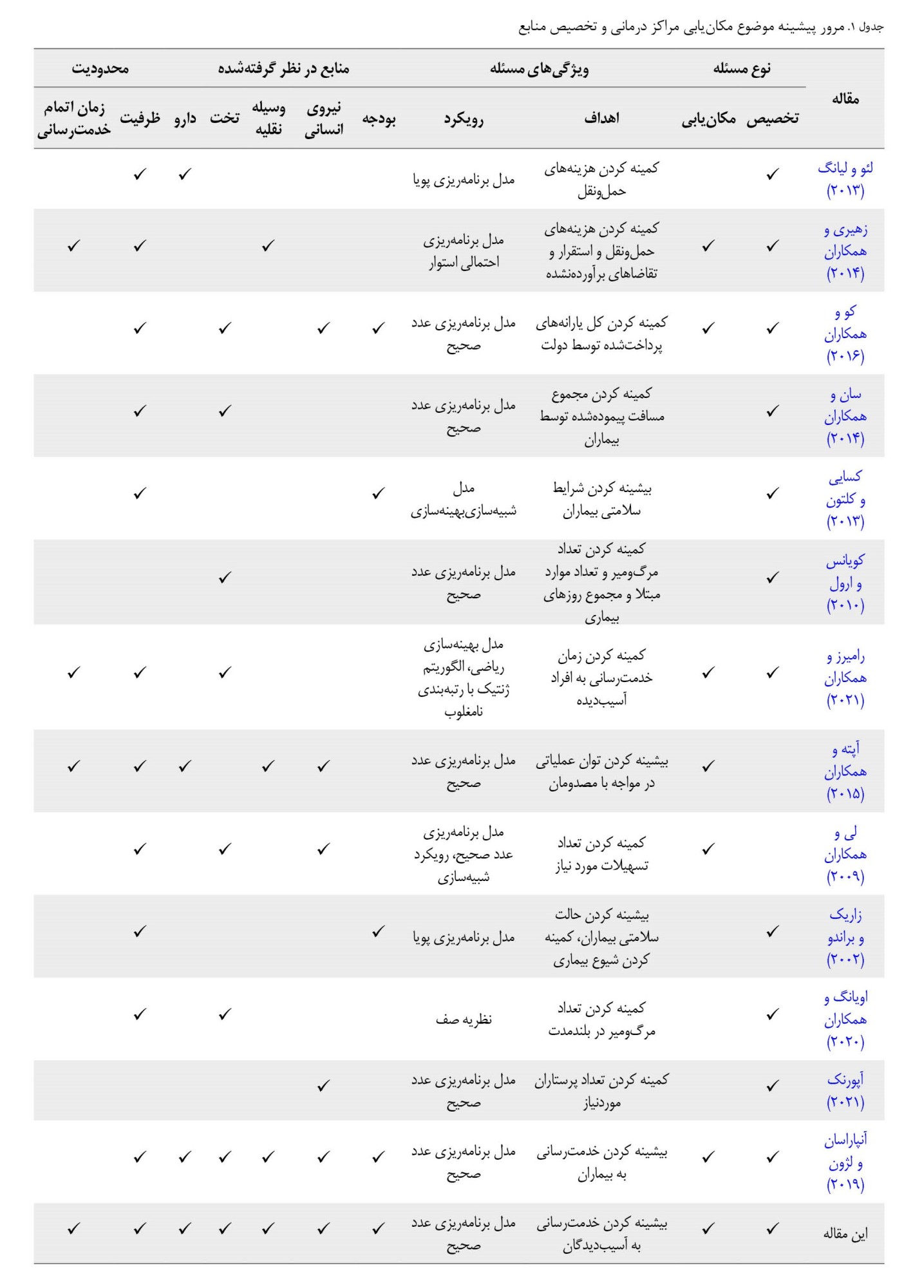
تصویر شماره 1 نمای گرافیکی از مسئله موردنظر را نشان میدهد.
 مجموعهها
مجموعهها
I: مجموعه نواحی آسیبدیده؛
J1: مجموعه بیمارستانهای دارای ظرفیت پذیرش آسیبدیدگان در اطراف نواحی آسیبدیده؛
J2: مجموعه مکانهای منتخب برای احداث بیمارستان صحرایی؛
Ij: مجموعه نواحی آسیبدیدهای که در فاصله زمانی مجاز نسبت به بیمارستان j قرار دارند؛
J1: مجموعه بیمارستانهایی که در فاصله زمانی مجاز نسبت به ناحیه آسیبدیده i قرار دارند؛
R: مجموعه انواع پرسنل پزشکی (پزشک و پرستار)؛
K: مجموعه آمبولانسها؛
L: مجموعه انواع بیمارستانهای صحرایی (چادری، کانکسی، ترکیبی)؛
پارامترها
P
1: جمعیت ناحیه آسیبدیده i؛
̃θ
i: شدت تخریب ناحیه i؛
t
ij: مدتزمان سفر آمبولانس از ناحیه آسیبدیده i تا بیمارستان j (بر حسب ساعت)؛
γ
ij: مدتزمان اضافی که آمبولانس برای رفتوبرگشت از ناحیه آسیبدیده i به بیمارستان j به دلایل مختلف ازجمله زمان سرویس، سوختگیری و ترافیک بایستی صرف کند (برحسب ساعت)؛
T: مدت زمان افق برنامهریزی ( بر حسب ساعت)؛
B: مقدار بودجه در دسترس برای احداث بیمارستان صحرایی؛
cb
l: تعداد تختهای بیمارستان صحرایی نوع l؛
h
l: هزینه احداث بیمارستان صحرایی نوع l؛
e
l: ظرفیت داروی پزشکی صحرایی نوع l؛
c
l: ظرفیت پذیرش بیمارستان j برای آسیبدیدگان jϵJl1؛
ca
k: ظرفیت آمبولانس k برای حمل آسیبدیدگان؛
q: تعداد آمبولانسهای موجود؛
m
r: تعداد پرسنل پزشکی در دسترس نوع r؛
u
r: تعداد آسیبدیدگانی که پرسنل پزشکی نوع r در هر روز میتوانند خدمترسانی کنند؛
n-minl
r: حداقل تعداد پرسنل پزشکی نوع r که برای بیمارستان صحرایی نوع l مورد نیاز است؛
n-maxl
r: حداکثر تعداد پرسنل پزشکی نوع r که برای بیمارستان صحرایی نوع l مورد نیاز است؛
β: درصدی از تختهای بیمارستانهای صحرایی که به سایر خدمات اورژانسی (همانند آپاندیسیت) و یا آسیبدیدگان انتقالی به بیمارستان با وسیلهای به غیر از آمبولانس (فرضاً با وسیله شخصی) اختصاص داده میشود؛
متغیرها
s
ijk: تعداد افراد آسیبدیده که از ناحیه آسیبدیده i بهوسیله آمبولانس k به بیمارستان واقع در گره j منتقل میشوند ((jϵJ
i؛
x
jl: متغیر صفر و 1: اگر بیمارستان صحرایی نوع l در گره منتخب j استقرار یابد، 1 و در غیر این صورت صفر است. ((jϵJ
2؛
y
ik: متغیر صفر و 1: اگر آمبولانس k به ناحیه آسیبدیدهتخصیص داده شود، 1 و در غیر این صورت صفر است؛
w
ijk: تعداد سفرهای آمبولانس k که از ناحیه آسیبدیده i به بیمارستان واقع درگره j انجام میشود؛
z
jr: تعداد پرسنل پزشکی نوع r که به بیمارستان صحرایی واقع در گره کاندید j تخصیص مییابد ((jϵJ
2؛
مدل ریاضی
جدول شماره 2 مدل ریاضی پیشنهادی را نشان میدهد که از نوع مدل یرنامهریزی عدد صحیح است. فرمول شماره 1، تابع هدف مدل و فرمولهای شماره 2 تا 22 محدودیتهای مدل را نشان میدهند. در ادامه به شرح تابع هدف و محدودیتهای موردنظر پرداخته میشود.

تابع هدف 1، بهمنظور بیشینهسازی مجموع مصدومان منتقلشده به بیمارستانها است. محدودیت 2 تضمین میکند که مجموع آسیبدیدگانی که از یک ناحیه آسیبدیده با آمبولانسها به بیمارستانها منتقل میشوند، نمیتواند بیشتر از تعداد آسیبدیدگان آن ناحیه باشد. محدودیت 3 به این نکته اشاره دارد که مجموع آسیبدیدگان پذیرششده در یک بیمارستان صحرایی، نباید از تعداد آسیبدیدگانی که پرسنل پزشکی در طول افق برنامهریزی میتوانند به آنها خدمترسانی کنند، بیشتر باشد. محدودیت 4 تضمین میکند که مجموع آسیبدیدگانی که به یک بیمارستان فعال در اطراف ناحیه آسیبدیده منتقل میشوند، نباید از ظرفیتی که آن بیمارستان برای پذیرش آسیبدیدگان این بحران تعیین کرده است، بیشتر باشد.
محدودیت 5 بیان میکند که مجموع تعداد آسیبدیدگانی که با آمبولانس به یک بیمارستان صحرایی منتقل میشوند، از تعداد تختهایی که برای این منظور در نظر گرفته شده است، بیشتر نباشد. محدودیت 6 مقدار بودجه در دسترس برای احداث بیمارستانهای صحرایی را در نظر میگیرد.
محدودیت 7 تضمین میکند که آمبولانس در هر سفر، حداکثر به اندازه ظرفیت خود میتواند آسیبدیدگان را حمل کند. محدودیت 8 یک حد بالا برای تعیین تعداد سفرهای آمبولانسها در نظر میگیرد. محدودیت 9 تضمین میکند که در هر گره منتخب، حداکثر 1 نوع بیمارستان صحرایی میتواند استقرار یابد. محدودیت 10 به این نکته اشاره دارد که آسیبدیدگان به شرطی میتوانند به بیمارستان صحرایی منتقل شوند که داروی کافی برای درمان آنها در دسترس باشد. محدودیت 11 بیان میکند که آمبولانسها حداکثر تا افق برنامهریزی، فرصت خدمترسانی به آسیبدیدگان را دارند. محدودیت 12 اطمینان حاصل میکند که تعداد آمبولانسهای تخصیصیافته به نواحی آسیبدیده از تعداد آمبولانسهای موجود بیشتر نباشد. محدودیت 13 تضمین میکند که هر آمبولانس به بیش از یک ناحیه آسیبدیده تخصیص داده نشود. محدودیتهای 14 و 15 مشخص میکنند که حدود بالا و پایین برای تعیین تعداد پرسنل در دسترس بیشتر نشود. محدودیت 17 تضمین میکند که اگر آمبولانس k هیچیک از آسیبدیدگان ناحیه i را به بیمارستانها منتقل نکند، آمبولانس k نمیتواند به ناحیه i تخصیص پیدا کند. محدودیتهای 18 تا 22 نیز دامنه متغیرها را نشان میدهند.
مطالعه موردی: شهر آمل
زلزله یکی از سوانح طبیعی است که همواره تهدیدی برای انسان بوده و به تلفات انسانی و خسارات مالی منجر میشود. کشور ایران نیز از این قاعده مستثنی نبوده است. براساس پایگاه داده بین المللی سوانح، از سال 2000 میلادی به بعد، کشور ایران با 55 مورد زلزله مواجه بوده است که مجموعاً به مصدوم شدن بیش از 46000 نفر و فوت بیش از 28000 نفر منجر شده است. بیشتر این آمار مربوط به زلزله بم بوده که به بزرگی 6/6 ریشتر در سال 1382 در شهر بم استان کرمان رخ داد و به مصدوم شدن بیش از 22000 نفر و فوت بیش از 26000 نفر منجر شد (
پایگاه داده بینالمللی سوانح، 2023).
یکی از استانهایی که در شمال ایران قرار دارد، استان مازندران است که در مجاورت رشتهکوه زاگرس قرار دارد و به دلیل قرار گرفتن روی گسل شمال البرز، از نواحی زلزلهخیز کشور به شمار میرود. شهر آمل بعد از ساری پرجمعیتترین شهر استان مازندران به حساب میآید که حدود 270000 نفر جمعیت دارد و در معرض خطر زلزله است. همچنین، شهر آمل بزرگترین قطب صنعتی استان مازندران بوده و به دلیل موقعیت استراتژیک و جغرافیایی به خاطر وجود جنگلهای انبوه، وصل بودن به جاده تهران ـ شمال، همجواری با استان تهران و چند راه ارتباطی تهران با شهرستانهای دیگر استان مازندران و همچنین توریستپذیر بودن، یکی از شهرهای مهم استان مازندران محسوب میشود. بنابراین برنامهریزی صحیح و مناسب، جهت پیشگیری یا کاهش آثار خطر احتمالی و تشکیل ستاد مدیریت بحران در این شهر و آمادگی لازم جهت امدادرسانی صحیح و کارآمد بسیار حیاتی و مهم است. ازاینرو، در این پژوهش شهر آمل بهعنوان مطالعه موردی در نظر گرفته شده و مدل ارائهشده روی این شهر اعمال شد.
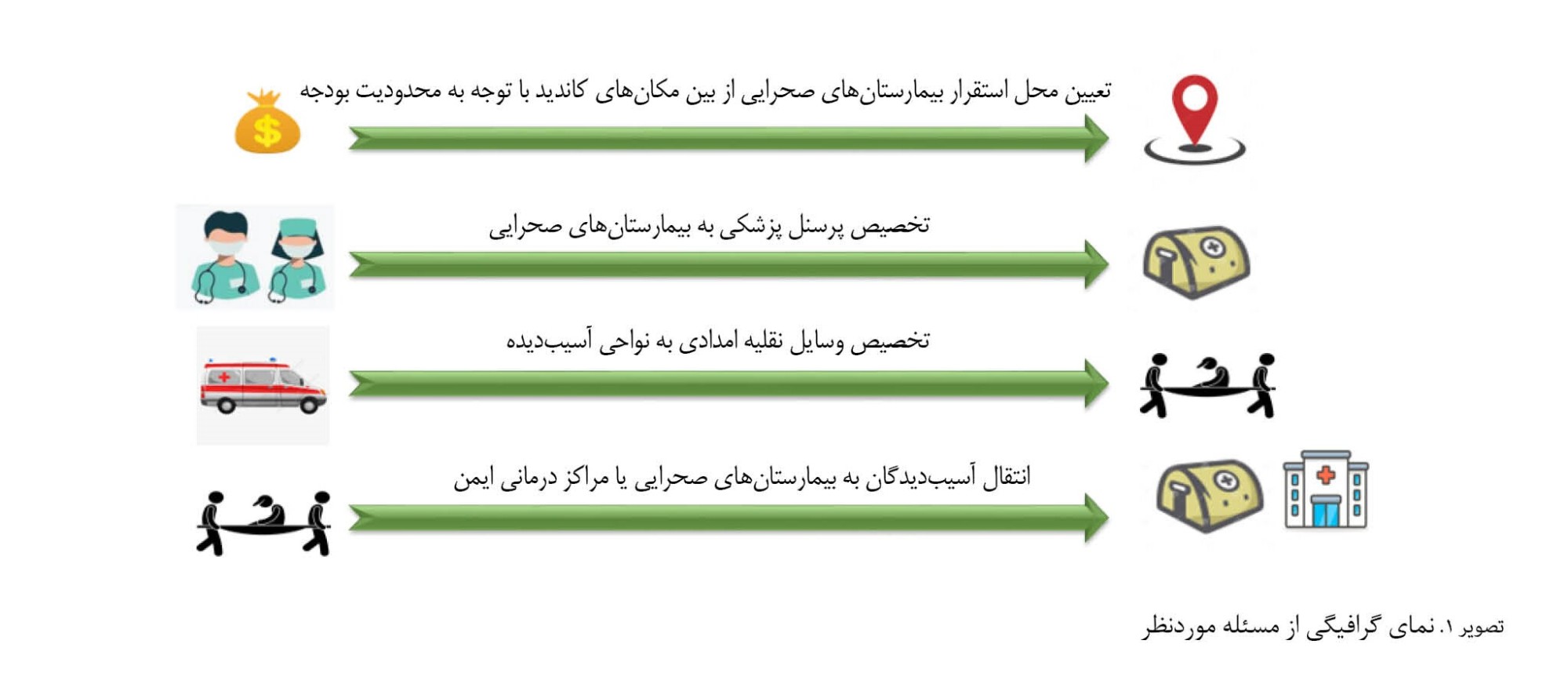
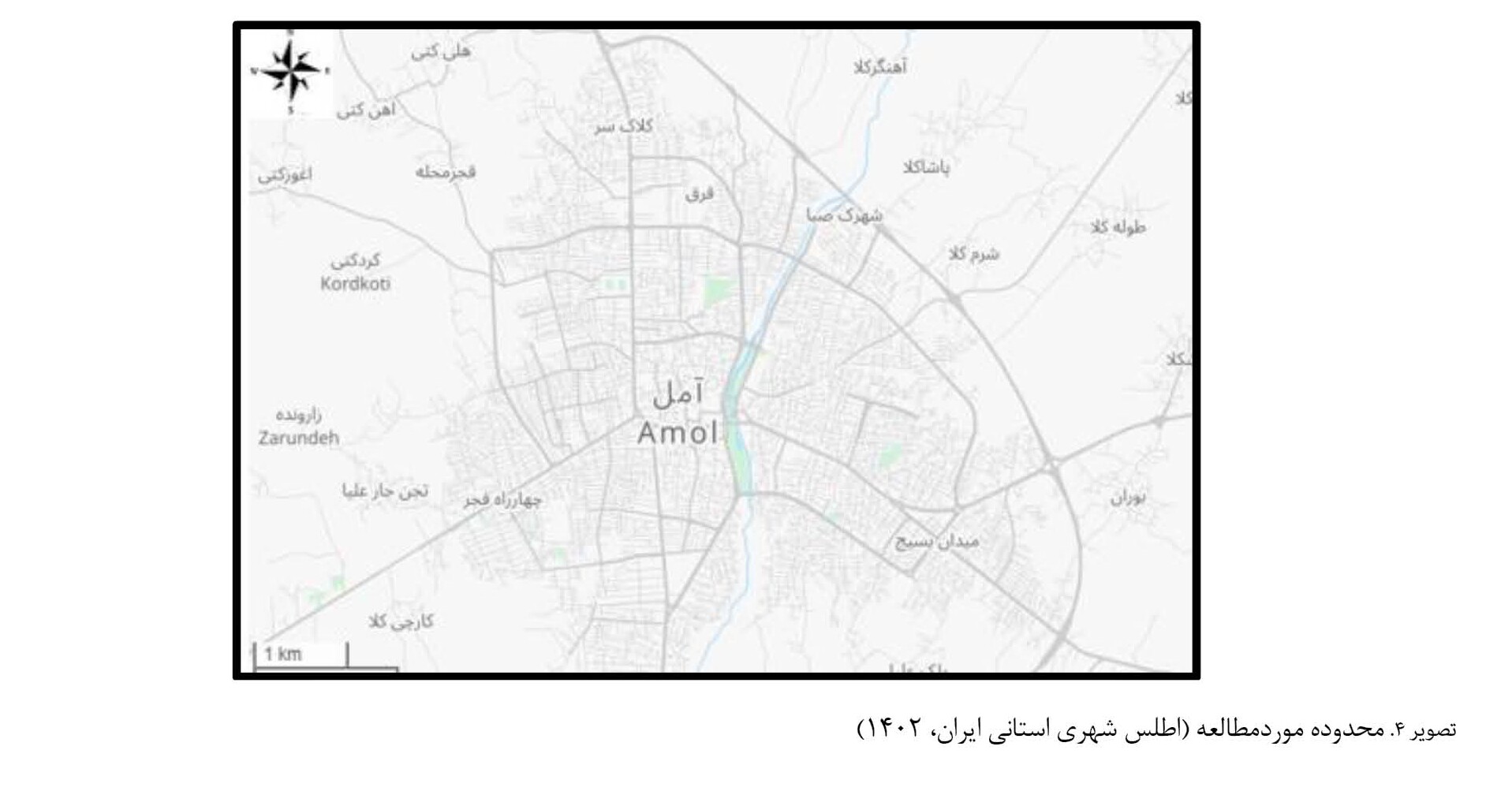
تصویرهای شماره 2،
3 و
4 به ترتیب، موقعیت استان مازندران در ایران، موقعیت شهر آمل در استان مازندران و محدوده موردمطالعه را نشان میدهد.
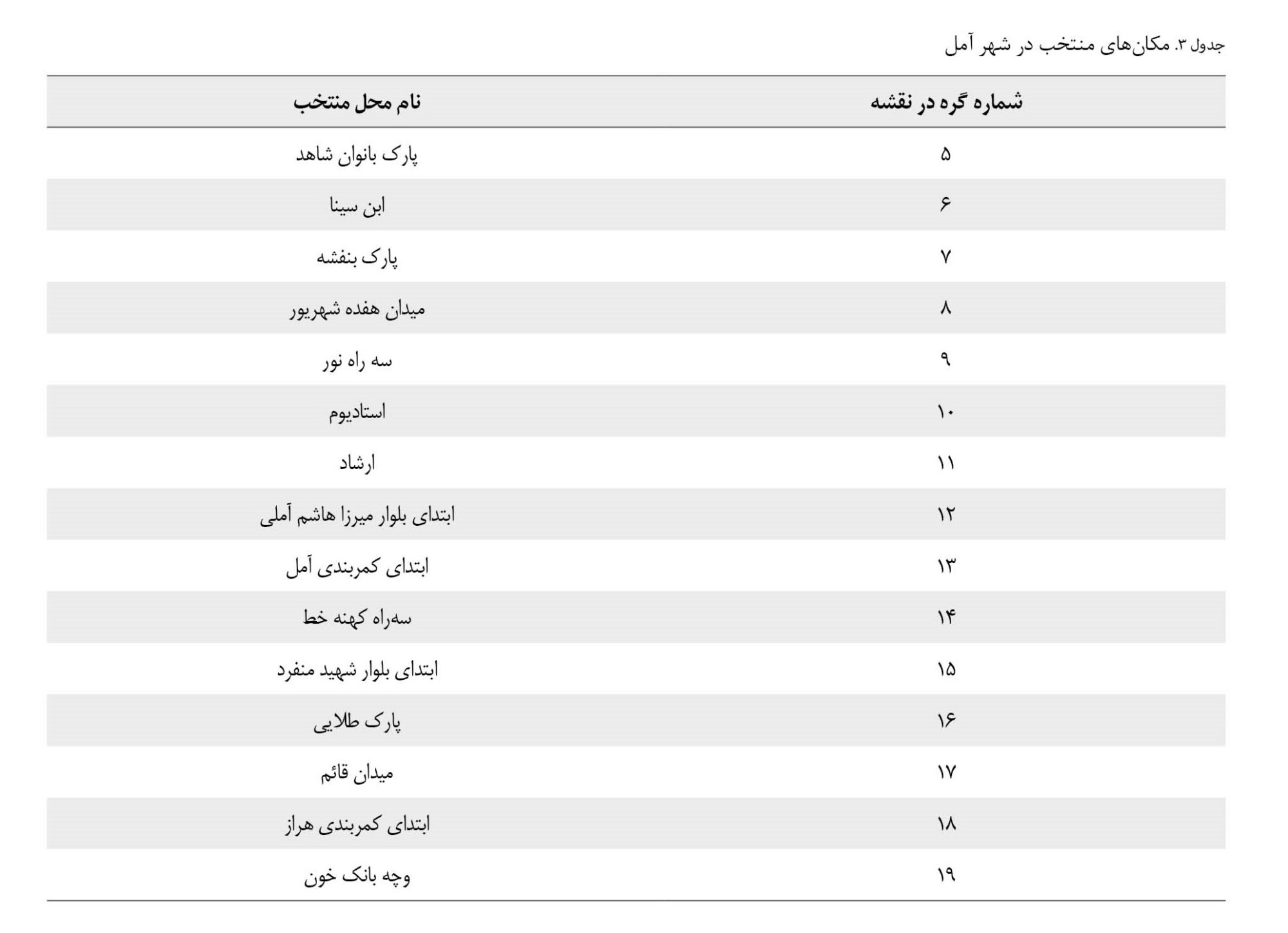
تعیین نواحی آسیبدیده و مکانهای منتخب برای احداث بیمارستانهای صحرایی در شهر آمل، از مهمترین اطلاعاتی بود که برای ارزیابی مدل ریاضی پیشنهادی، لازم بود تهیه شوند. در مطالعه
ملا داوودی و همکاران (1394) 15 محل منتخب برای احداث بیمارستانهای صحرایی در شهر آمل مشخص شدهاند که در پژوهش حاضر همان 15 محل بهعنوان مکانهای مدنظر انتخاب شدند (محل دقیق این مکانها در
جدول شماره 3 شرح داده شده است).
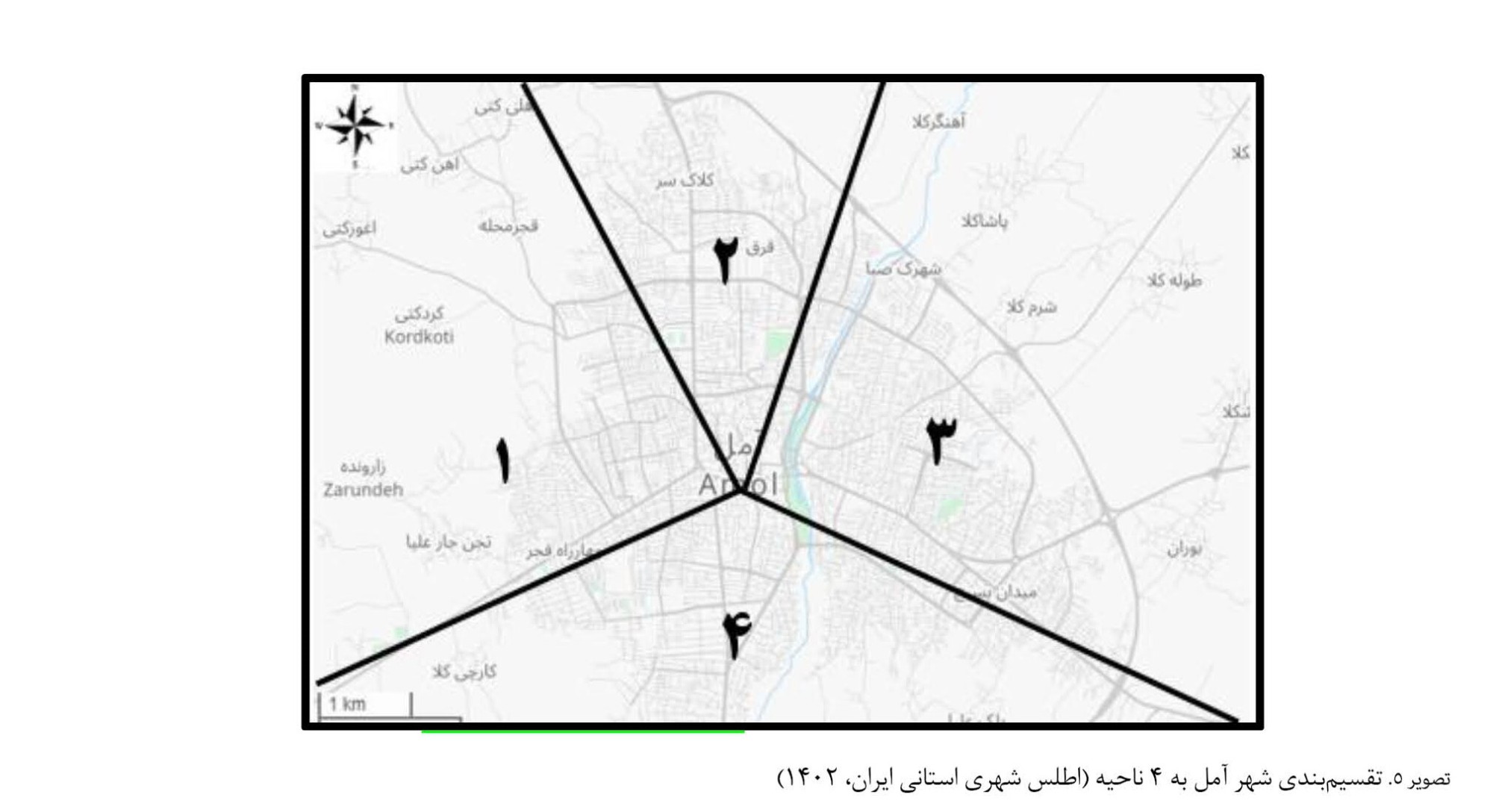
همچنین آنها شهر آمل را مطابق
تصویر شماره 5 به
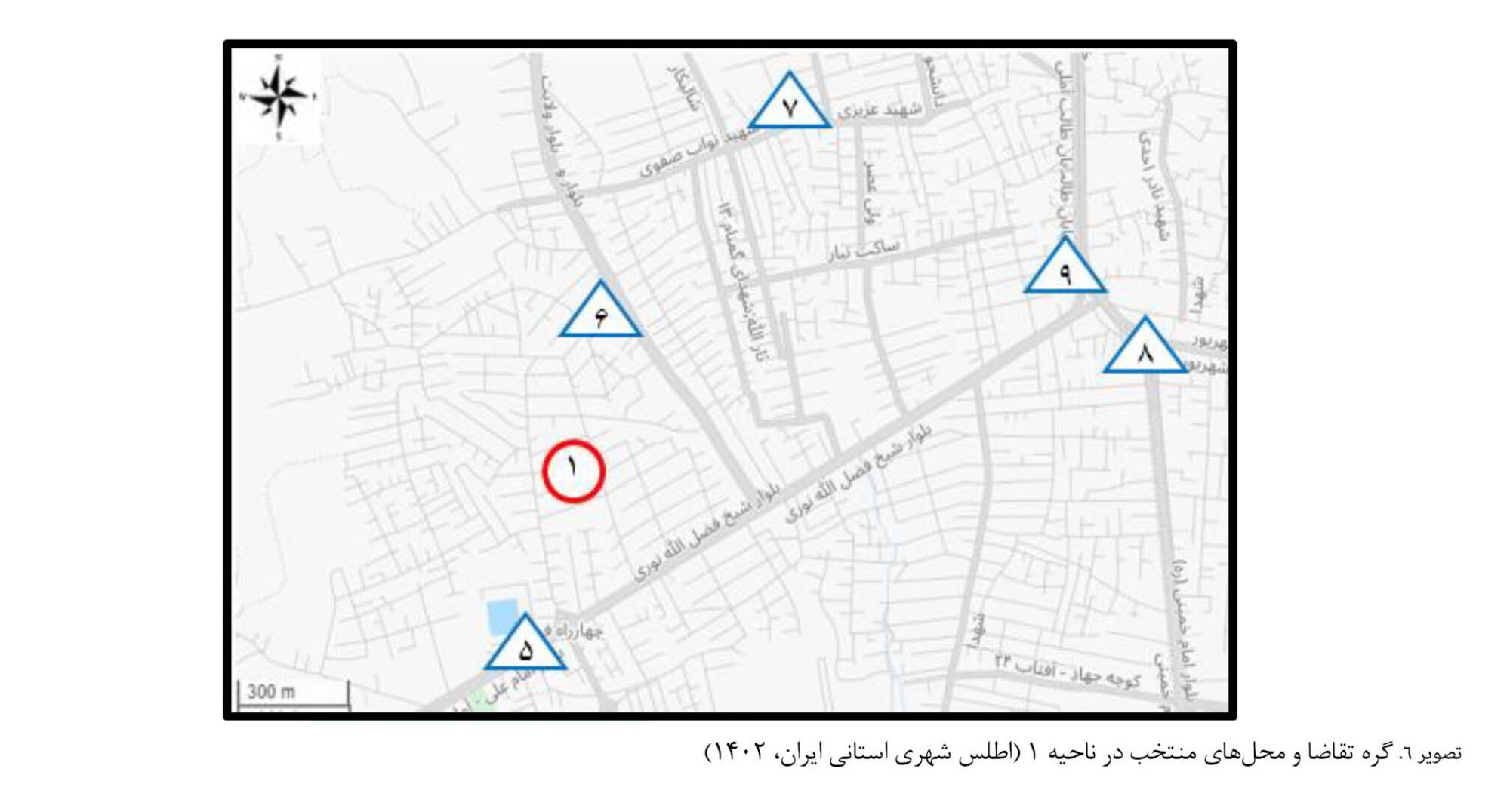
4 ناحیه تقسیمبندی میکنند که در پژوهش حاضر نیز همان 4 ناحیه بهعنوان نواحی آسیبدیده در نظر گرفته شدند. برای تعیین فاصله زمانی بین نواحی آسیبدیده تا مراکز درمانی، در هر ناحیه، گرهی بهعنوان گره تقاضا بهصورت فرضی در نظر گرفته شد و فاصله زمانی بین گرهها با کمک نرمافزار گوگلمَپ به دست آمد.
 تصویرهای شماره 6
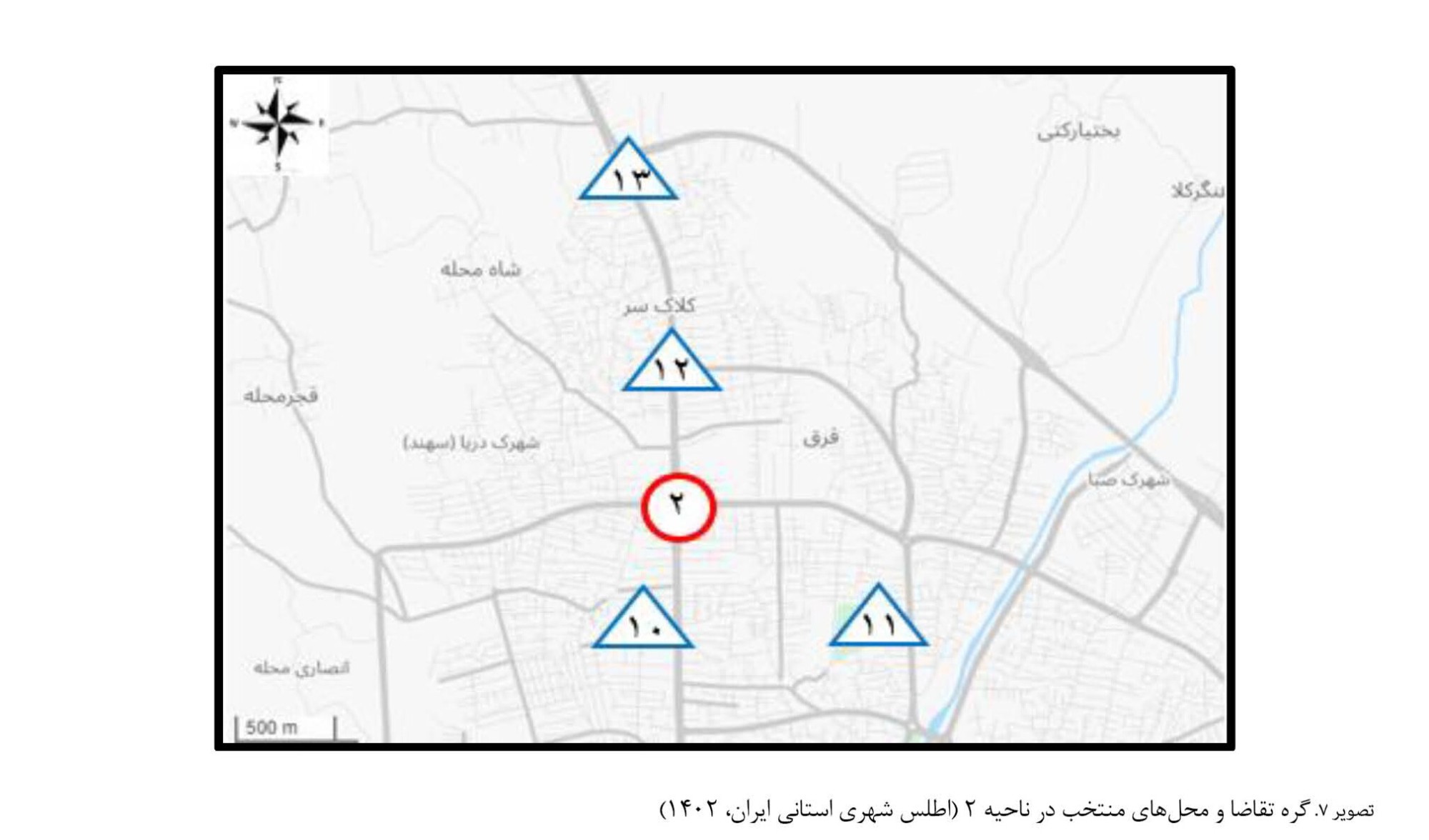
تصویرهای شماره 6،
7،
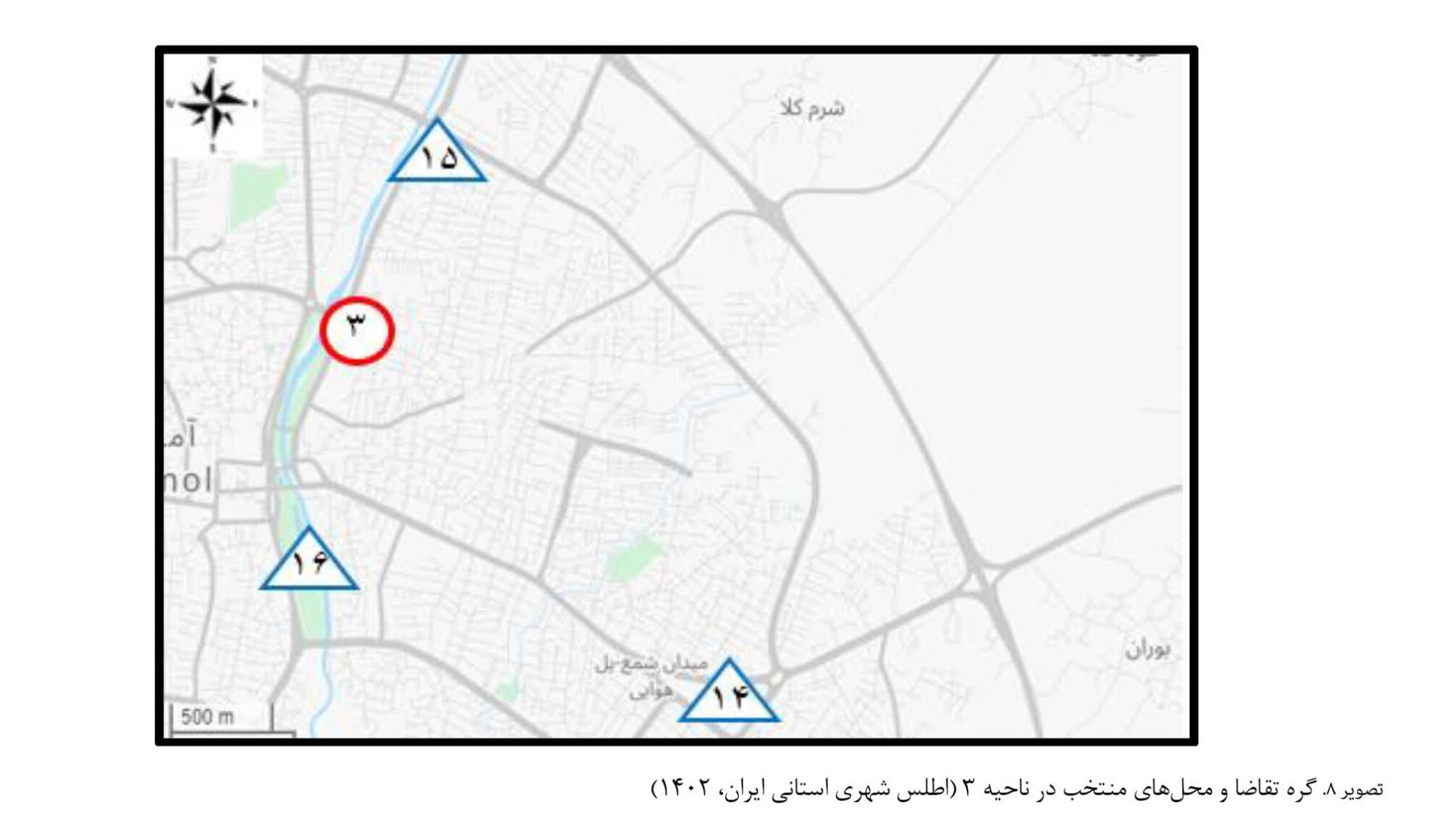
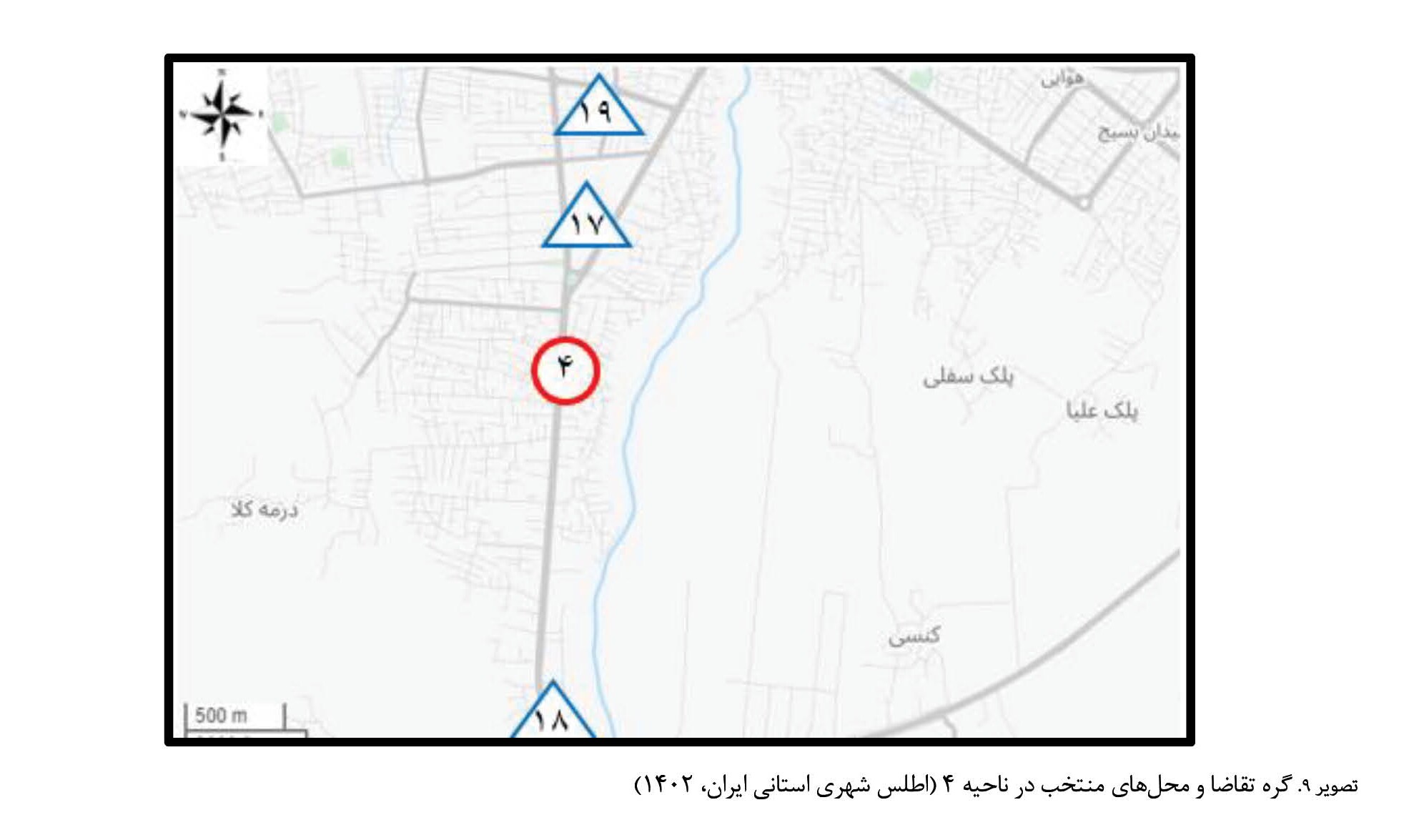
8 و
9، گرههای تقاضا (گرههای 1 تا 4) و مکانهای منتخب (گرههای 5 تا 19) را در نقشه برای نواحی 1 تا 4 به ترتیب نشان میدهند.
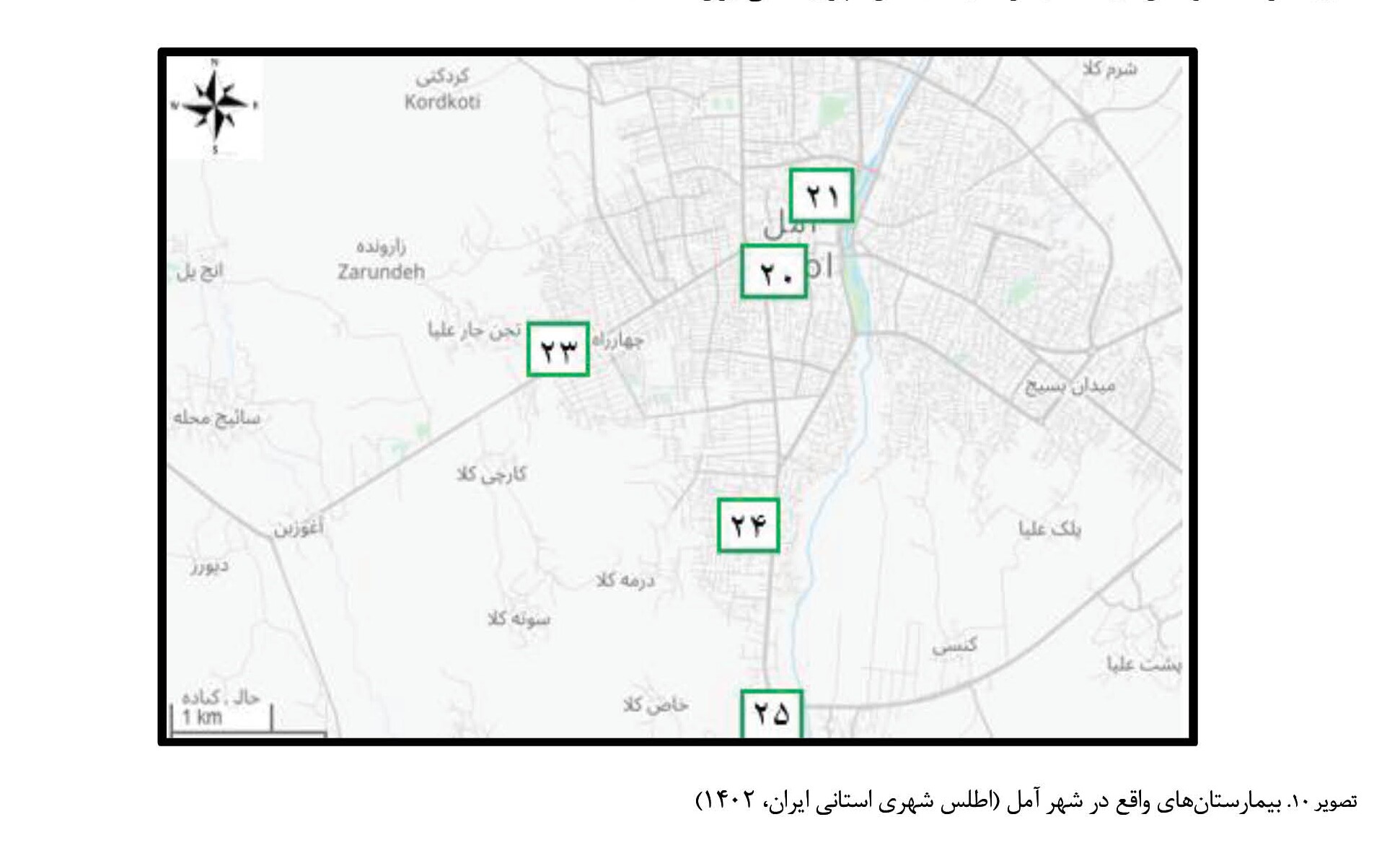
 تصویر شماره 10
تصویر شماره 10 نیز محل بیمارستانهای واقع در شهر آمل (گرههای 20 تا 24) را در نقشه نشان میدهد. در
جدول شماره 4 اسامی این 5 بیمارستان و شماره گره آنها در نقشه آمده است.

فاصله زمانی مجاز برای انتقال آسیبدیدگان به بیمارستانها 0/5 ساعت در نظر گرفته شده است.
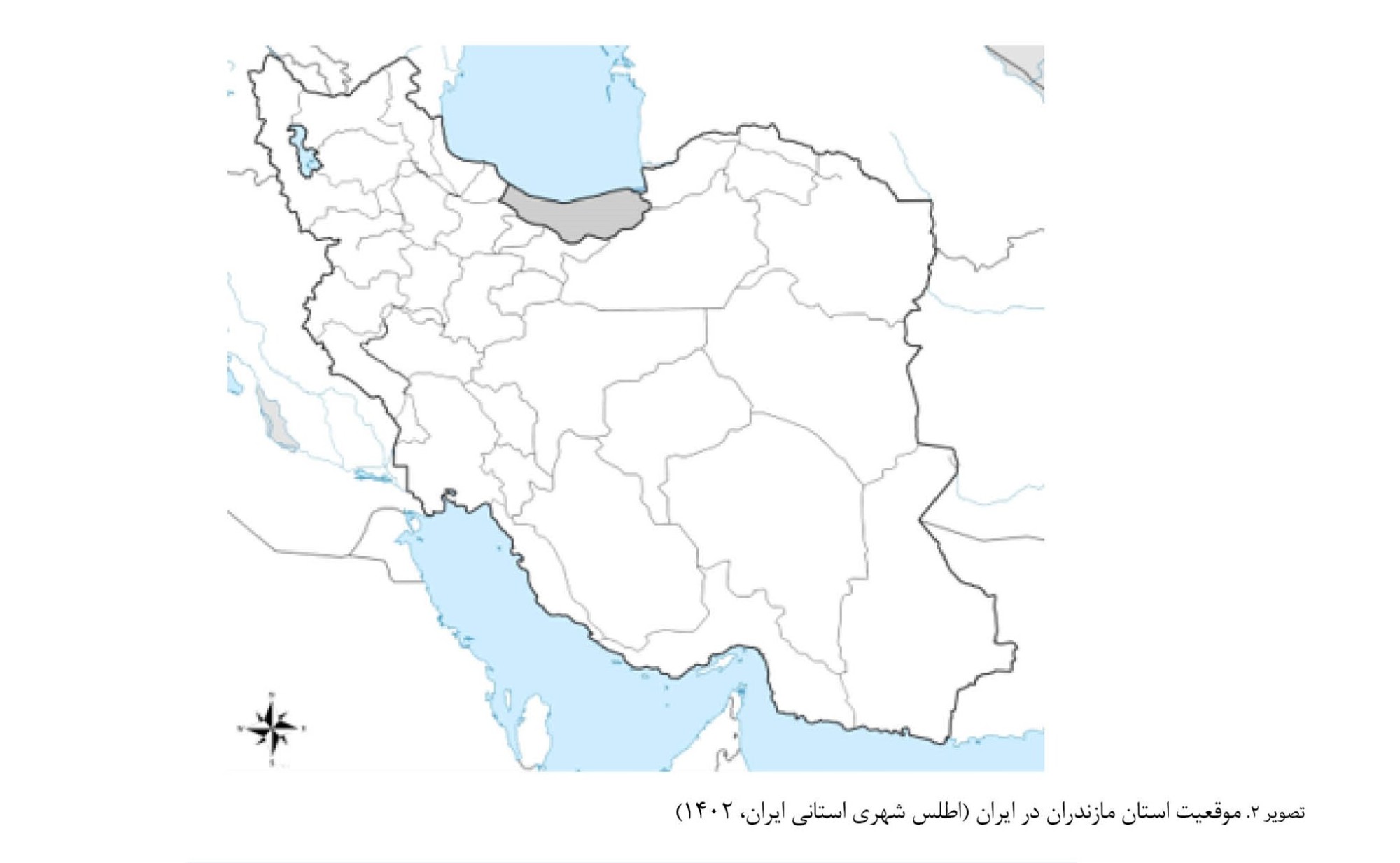
همچنین شدت تخریب هر ناحیه (̃θi) بهصورت یک عدد فازی مثلثی (θ
1(i), θ
2(i), θ
3(i)) در نظر گرفته شد و با استفاده از فرمول شماره (23) قطعی شدهاند (
راس، 2009).
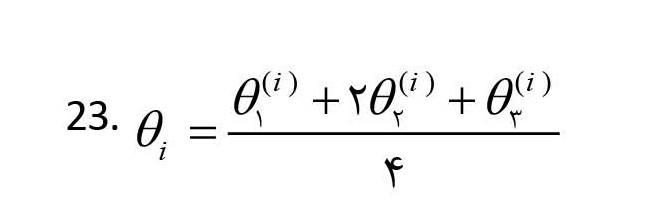
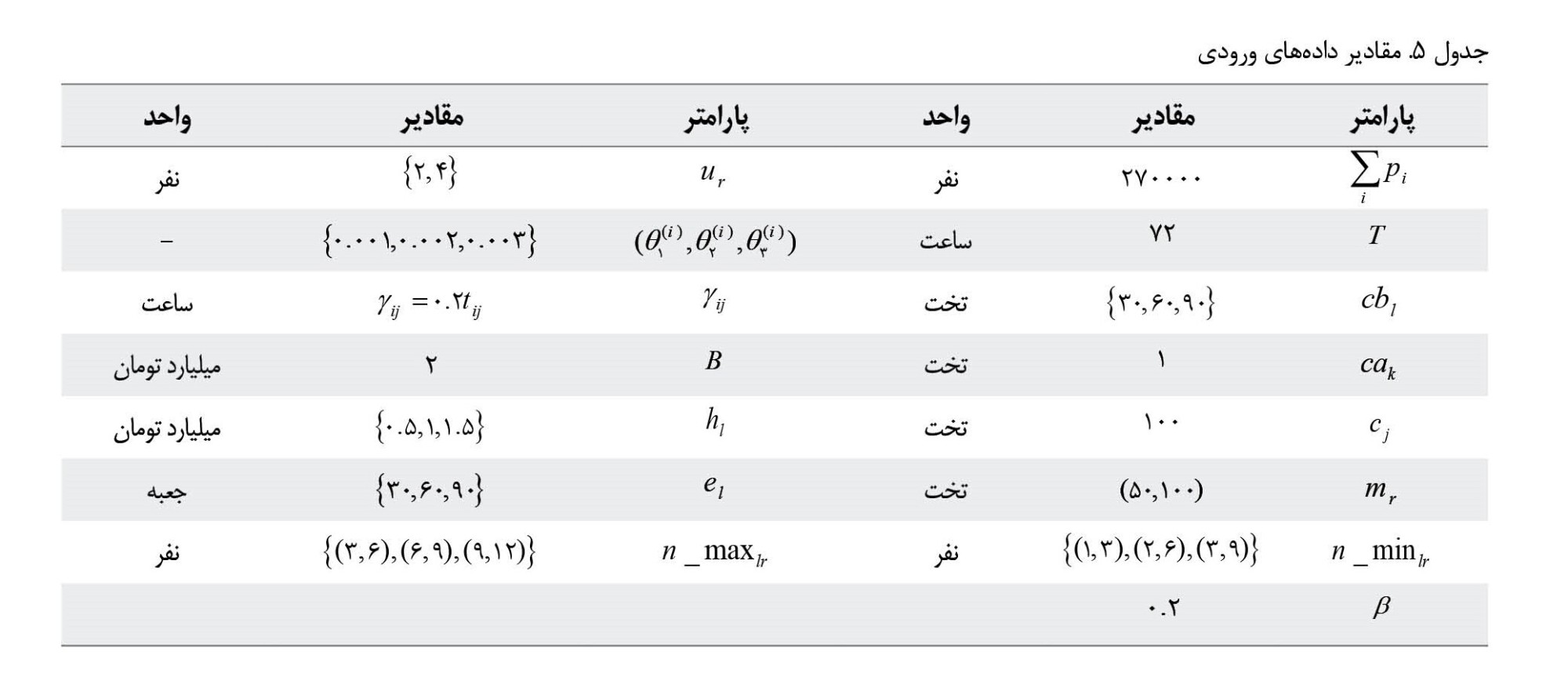
مقادیر سایر دادههای موردنیاز بهصورت فرضی ولی منطقی درنظر گرفته شدهاند که در
جدول شماره 5 قابلمشاهده است.
 یافتهها
یافتهها
پس از جمعآوری دادههای موردنیاز، مدل پیشنهادی در نرمافزار بهینهسازی گمز نسخه 25/1 و با حلکننده GUROBI در یک رایانه با مشخصات Intel i5-2.50 GHz و RAM 6 GB اجرا شد. خروجی نرمافزار گمز در
جدول شماره 6 قابلمشاهده است. بیمارستانهای صحرایی شامل انواع مختلفی هستند که 3 نمونه از آنها عبارتاند از: بیمارستانهای صحرایی چادری، کانکسی و ترکیبی (
آتشپنجه و همکاران، 1395).
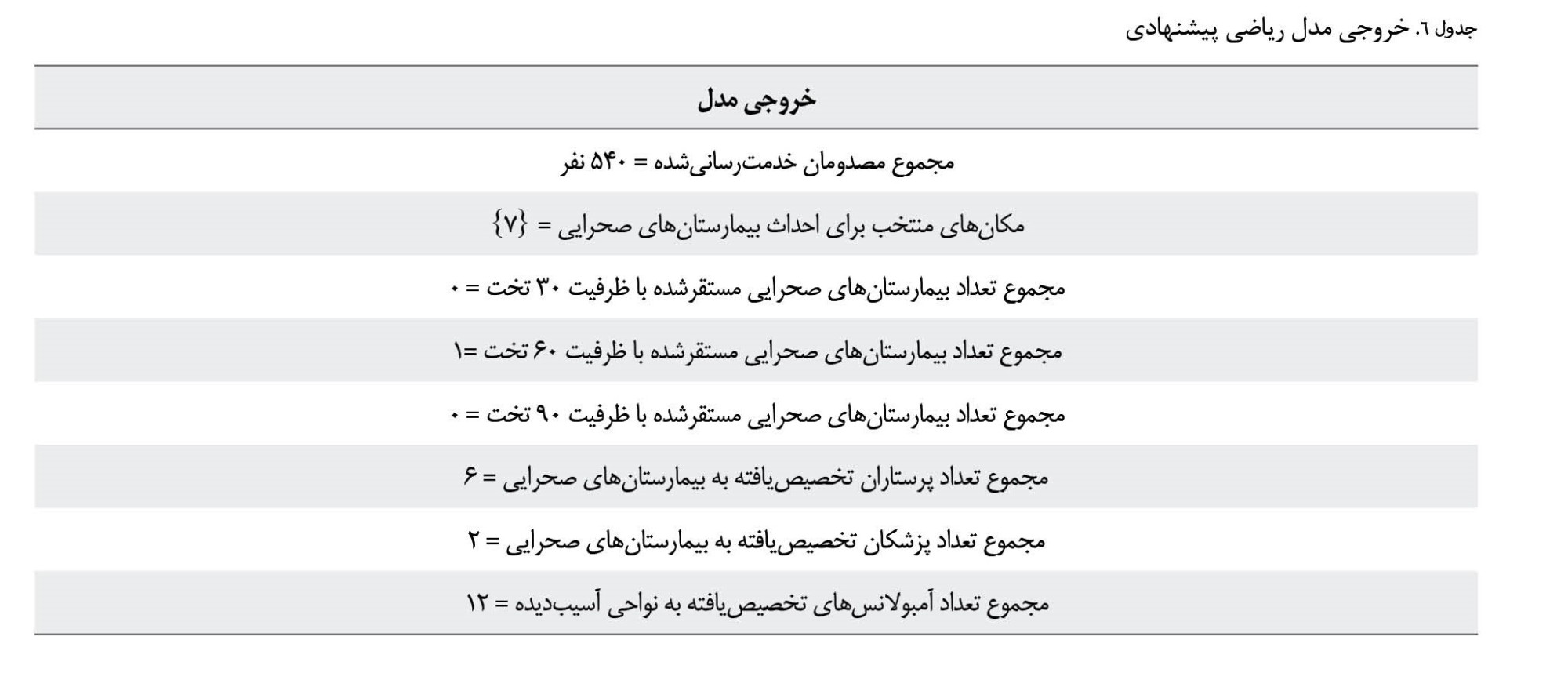
تفاوت عمده این بیمارستانها در هزینه احداث آنها و همچنین ظرفیتشان (تعداد تخت) برای پذیرش آسیبدیدگان است. در این پژوهش، فرض شده است بیمارستان صحرایی نوع اول، دوم و سوم به ترتیب دارای 30 تخت، 60 تخت و 90 تخت است. مکان بهینهای که برای احداث بیمارستان صحرایی مشخص شد، گره 7 یعنی همان پارک بنفشه است (
تصویر شماره 11). همچنین بیمارستان صحرایی که در گره 7 استقرار مییابد، باید از نوع دوم باشد.
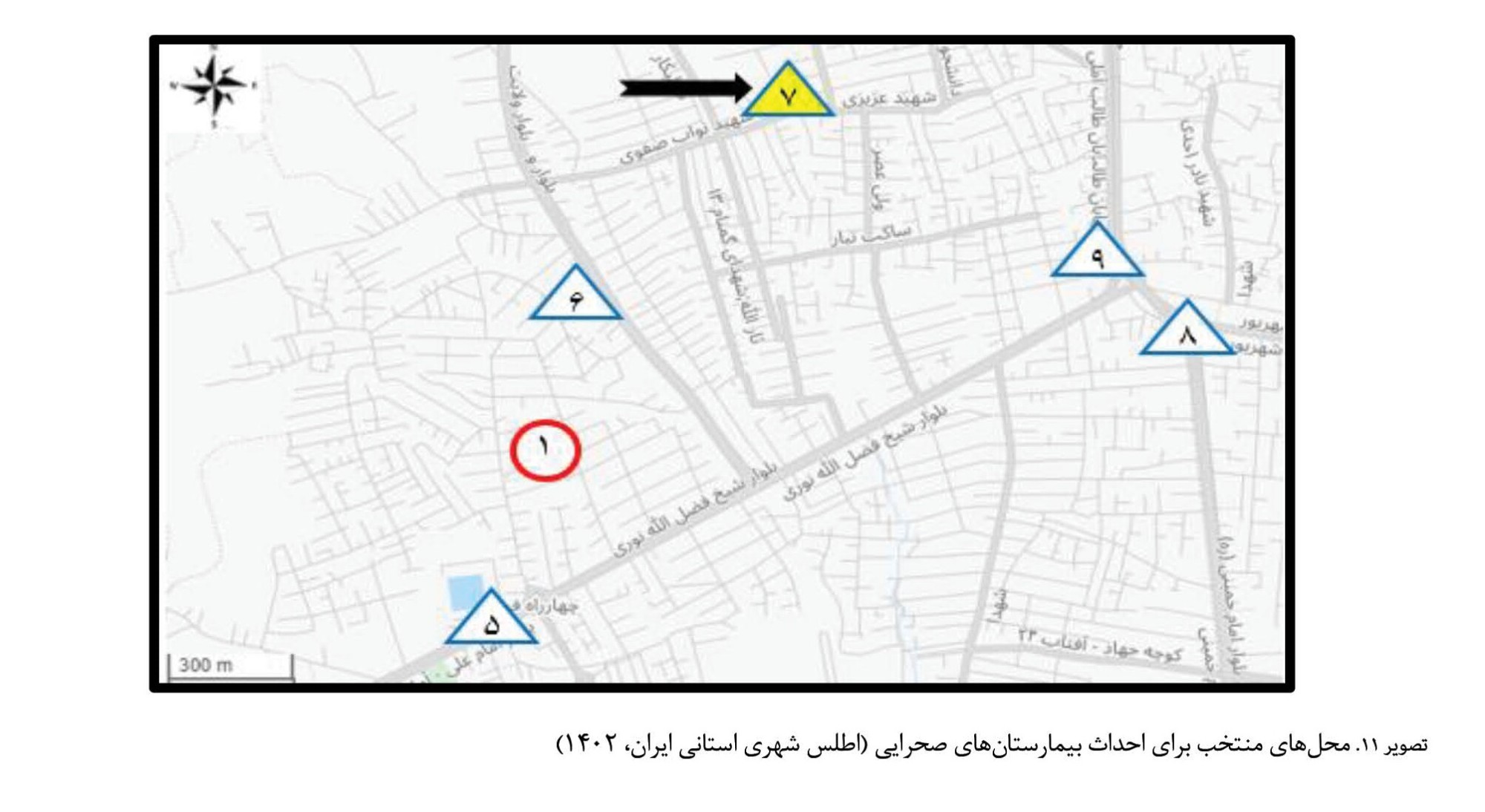
درواقع با ایجاد یک بیمارستان صحرایی تمام مصدومان (540 نفر) را میتوان در مدت 72 ساعت به بیمارستان منتقل کرد. اکنون سؤالی را میتوان مطرح کرد که «اگر شدت تخریب زلزله به گونهای باشد که تعداد مصدومان دو برابر شود (1080 نفر)، به چه بودجهای برای استقرار بیمارستانهای صحرایی نیاز است تا تمام مصدومان را در مدت 72 ساعت بتوان به مراکز درمانی منتقل کرد؟». برای پاسخ به این سؤال، تحلیل حساسیتی روی مقدار بودجه دردسترس و تعداد مصدومان خدمترسانیشده انجام شد. درواقع، مقدار بودجه در دسترس به تدریج اضافه شد تا خدمترسانی به همه مصدومان تکمیل شود.
تصویر شماره 12 نتایج تحلیل حسیاست را نشان میدهد. باتوجهبه
تصویر شماره 12 میتوان متوجه شد که با بودجه 13 میلیارد میتوان به تمام مصدومان خدمترسانی کرد. در این مثال فرض شد که هر 5 بیمارستان واقع در شهر آمل فعال هستند و پس از زلزله، تخریب نشده و میتوان از ظرفیت آنها برای بستری مصدومان استفاده کرد.
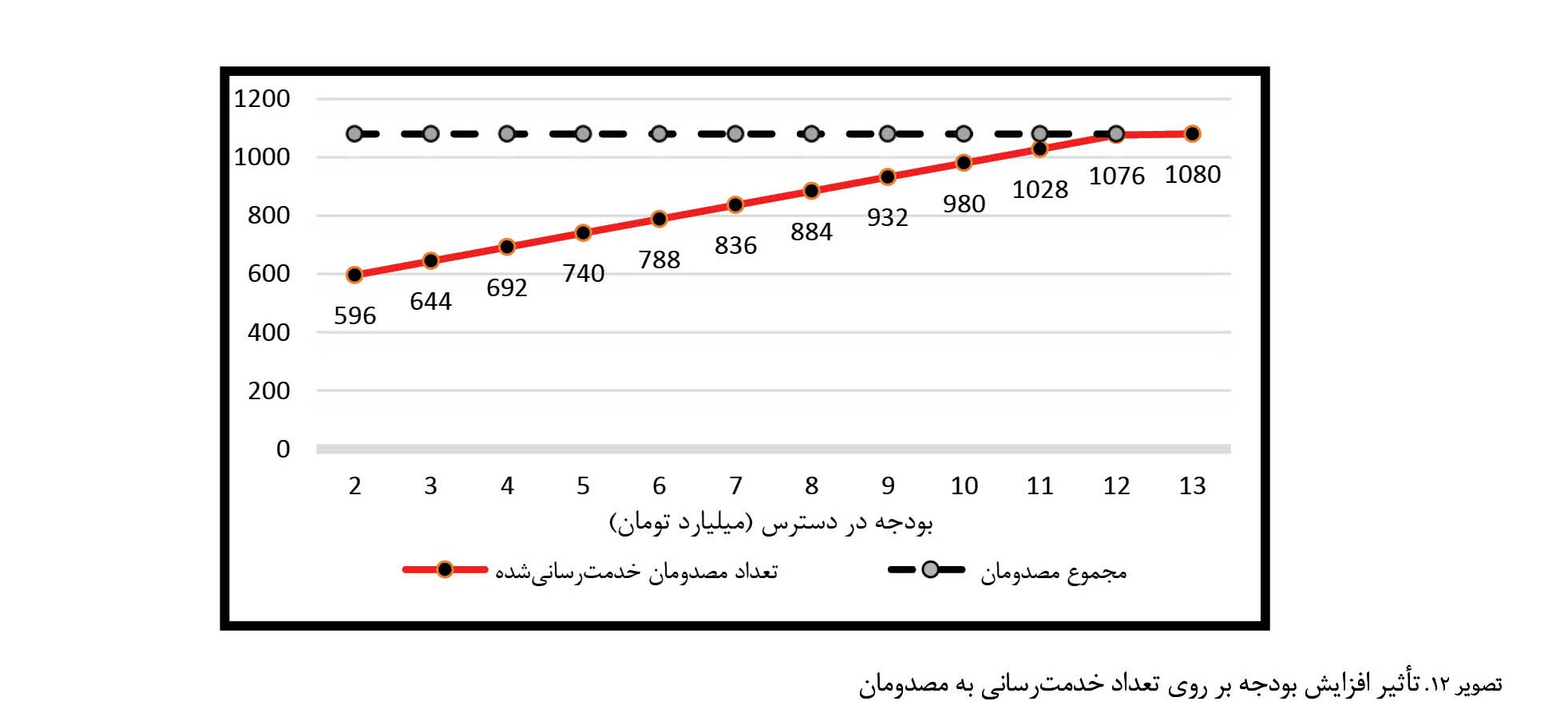
اکنون سؤال دیگری را میتوان در اینجا مطرح کرد که «اگر یکی از این 5 بیمارستان واقع در شهر آمل به دلیل شدت تخریب زلزله، غیرقابلاستفاده شوند، چه تغییری در تعداد و نوع بیمارستانهای صحرایی مستقرشده ایجاد خواهد شد؟». برای پاسخ به این سؤال، مدل پیشنهادی 5 بار اجرا شد که در هر اجرا یکی از 5 بیمارستان، غیرفعال و ظرفیت آن صفر در نظر گرفته شد.
تصویر شماره 13 نتایج این تحلیل حساسیت را نشان میدهد.
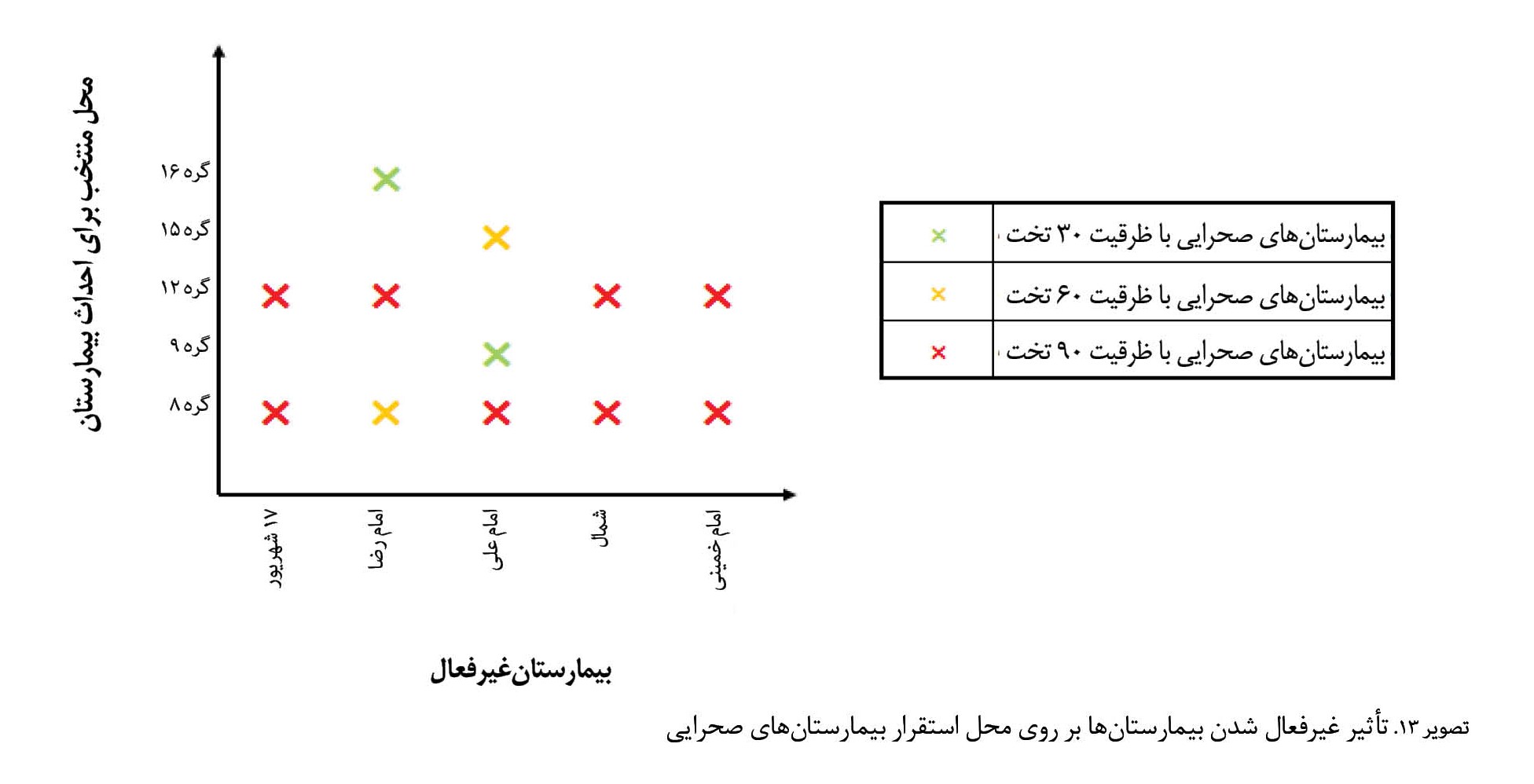
نتایج نشان میدهند اگر یکی از بیمارستانهای 17 شهریور، شمال و یا امام خمینی غیرفعال شود، 2 بیمارستان صحرایی نوع سوم (90 تخت) لازم است در گرههای 8 (میدان هفده شهریور) و 12 (ابتدای بلوار میرزا هاشم آملی) استقرار یابند. اگر بیمارستان امام رضا غیرفعال شود، 3 بیمارستان صحرایی از نوع اول (30 تخت)، دوم (60 تخت) و سوم (90 تخت) لازم است استقرار یابند که به ترتیب در گرههای 16 (پارک طلایی)، 8 (میدان هفده شهریور) و 12 (ابتدای بلوار میرزا هاشم آملی) جای میگیرند. اگر بیمارستان امام علی غیرفعال شود، 3 بیمارستان صحرایی از نوع اول (30 تخت)، دوم (60 تخت) و سوم (90 تخت) لازم است استقرار یابند که به ترتیب در گرههای 9 (سهراه نور)، 15 (ابتدای بلوار شهید منفرد) و 8 (میدان هفده شهریور) جای میگیرند. بهطورکلی میتوان نتیجه گرفت که گره 8 محل مناسبی برای احداث بیمارستان صحرایی است، زیرا در تمام 5حالت این گره انتخاب شده است.
بحث
در این پژوهش، شهر آمل که یکی از شهرهای پرجمعیت شهر مازندران محسوب میشود، بهعنوان مطالعه موردی انتخاب شده و مدل ریاضی پیشنهادی توسط دادههای مربوط به این شهر ارزیابی شده است. ضمناً فرض شده است که تمام بیمارستانهای واقع در شهر آمل بعد از سانحه طبیعی (زلزله) فعال بوده و تخریب نمیشوند. نتایج محاسباتی در این حالت نشان داد که بهترین مکان برای احداث بیمارستان صحرایی، در محوطه پارک بنفشه میباشد. ضمناً تحلیل حساسیتی بر روی مقدار بودجه دردسترس و تعداد مصدومان امدادرسانیشده انجام شد. نتایج نشان داد بودجه، تأثیر بسزایی در کیفیت خدمترسانی به مصدومان خواهد داشت.
در ادامه، فرض شد شدت تخریب زلزله بهگونهای است که یکی از بیمارستانهای شهر آمل تخریب شده و غیر فعال میشود. در این حالت نیز مشخص شد که یکی از مکانهای مناسب برای احداث بیمارستان صحرایی، میدان هفده شهریور میباشد.
نتیجهگیری
امروزه جهان بهدلیل تغییرات اقلیمی، زیستی و فناوری با افزایش تعداد و تنوع سوانح مواجه است. در میان چالشهایی که بعد از وقوع یک سانحه به وجود میآید، مسئله مکانیابی بیمارستانهای صحرایی و تخصیص منابع پزشکی از اهمیت ویژهای برخوردار است. بدینمنظور در این تحقیق یک مدل برنامهریزی عدد صحیح مختلط پیشنهاد شده است که محدودیتهای مختلفی مانند محدودیت در بودجه احداث بیمارستانهای صحرایی، ظرفیت بیمارستانها برای پذیرش آسیبدیدگان سانحه، تعداد آمبولانسها، تعداد پرسنل پزشکی و مقدار داروهای پزشکی دردسترس، در این مدل در نظر گرفته شده است. در این پژوهش، مکانیابی بیمارستانهای صحرایی باتوجهبه بیمارستانهای فعال در اطراف نواحی آسیبدیده انجام شده است. بنابراین آسیبدیدگان علاوه بر بیمارستانهای صحرایی احداثشده، به بیمارستانهای فعال نیز میتوانند منتقل شوند. همچنین محدودیتی برای اتمام زمان خدمترسانی اعمال شده. بهطوریکه وسایل نقلیه امدادی در مدتزمان محدودی، فرصت انتقال مصدومان را به مراکز امدادی در اختیار دارند.
در این راستا مسئله مسیریابی وسایل نقلیه امدادی در زمان بحرانهایی، مانند زلزله که بسیاری از مسیرها مسدود میشود، میتواند بسیار مهم باشد. بنابراین یکی از مهمترین پیشنهادات برای توسعه مدل پیشنهادی، ارائه یک مدل مکانیابی ـ تخصیص ـ مسیریابی است. همچنین مدل پیشنهادی میتواند در شهرهای بزگتر و پرجمعیتتری مانند تهران و یا اصفهان ارزیابی شود.
ملاحظات اخلاقی
پیروی از اصول اخلاق پژوهش
در این پژوهش، اصول اخلاقی رعایت شده و شرکتکنندگان از تمام مراحل پژوهش آگاهی کامل داشتند.
حامی مالی
این مقاله حامی مالی ندارد.
مشارکت نویسندگان
همه نویسندگان بهطور یکسان در تهیه این مقاله مشارکت داشتند.
تعارض منافع
بنابر اظهار نویسندگان این مقاله تعارض منافع ندارد.
References
Akhtari, F., & Noorizadeh, R. (2006). [Field hospitals and their role in natural disasters (Persian)]. Paper presented at: 3rd International Congress on Health, Medication and Crisis Management in Disaster, Tehran, Iran, 22 November 2006. [Link]
Atash Panjeh, H., Dast Dadeh, F., & Porbin, Z. (2016). [Investigation of field hospitals from the point of view of passive defense (Persian)]. Paper presented at: National Conference on Passive Defense and Sustainable Development, Tehran, Iran, 15 October 2016. [Link]
Gitashenasi. (2023). [Atlas of Tehran (Persian)]. Retrieved from: [Link]
Liu, M., & Liang, J. (2013). Dynamic optimization model for allocating medical resources in epidemic controlling. Journal of Industrial Engineering and Management, 6(1), 73-88. [DOI:10.3926/jiem.663]
Moladavoodi, H., Paydar, M. M., & Safai, A. (2016). [Locating field hospitals with the approach of hierarchical analysis process (Persian)]. Paper presented at: The International Conference in New Research of Industry and Mechanical Engineering, Tehran, Iran, 16 February 2016. [Link]
Zahiri, B., Tavakkoli-Moghaddam, R., & Pishvaee, M. S. (2014). A robust possibilistic programming approach to multi-period location-allocation of organ transplant centers under uncertainty. Computers & Industrial Engineering, 74, 139-148. [DOI:10.1016/j.cie.2014.05.008]
Ko, Y. D., Song, B. D., & Hwang, H. (2016). Location, capacity and capability design of emergency medical centers with multiple emergency diseases. Computers & Industrial Engineering, 101, 10-20. [DOI:10.1016/j.cie.2016.08.011]
Sun, L., DePuy, G. W., & Evans, G. W. (2014). Multi-objective optimization models for patient allocation during a pandemic influenza outbreak. Computers & Operations Research, 51, 350-359. [DOI:10.1016/j.cor.2013.12.001]
Kasaie, P., & Kelton, W. D. (2013). Simulation optimization for allocation of epidemic-control resources. IIE Transactions on Healthcare Systems Engineering, 3(2), 78-93. [DOI:10.1080/19488300.2013.790717]
Dellaert, N., Cayiroglu, E., & Jeunet, J. (2016). Assessing and controlling the impact of hospital capacity planning on the waiting time. International Journal of Production Research, 54(8), 2203-2214. [DOI:10.1080/00207543.2015.1051668]
Ramirez-Nafarrate, A., Araz, O. M., & Fowler, J. W. (2021). Decision assessment algorithms for location and capacity optimization under resource shortages. Decision Sciences, 52(1), 142-181. [DOI:10.1111/deci.12418]
Apte, A., Heidtke, C., & Salmerón, J. (2015). Casualty collection points optimization: A study for the district of Columbia. Interfaces, 45(2), 149-165. [DOI:10.1287/inte.2014.0757]
Lee, E. K., Smalley, H. K., Zhang, Y., Pietz, F., & Benecke, B. (2009). Facility location and multi-modality mass dispensing strategies and emergency response for biodefence and infectious disease outbreaks. International Journal of Risk Assessment and Management, 12(2-4), 311-351. [DOI:10.1504/IJRAM.2009.025925]
Zaric, G. S., & Brandeau, M. L. (2002). Dynamic resource allocation for epidemic control in multiple populations. Mathematical Medicine and Biology: A Journal of the IMA, 19(4), 235-255. [DOI:10.1093/imammb/19.4.235]
Ouyang, H., Argon, N. T., & Ziya, S. (2020). Allocation of intensive care unit beds in periods of high demand. Operations Research, 68(2), 591-608. [DOI:10.1287/opre.2019.1876]
Koyuncu, M., & Erol, R. (2010). Optimal resource allocation model to mitigate the impact of pandemic influenza: A case study for Turkey. Journal of Medical Systems, 34(1), 61-70. [DOI:10.1007/s10916-008-9216-y] [PMID]
Apornak, A. (2021). Human resources allocation in the hospital emergency department during COVID-19 pandemic. International Journal of Healthcare Management, 14(1), 264-270. [DOI:10.1080/20479700.2020.1861173]
Anparasan, A., & Lejeune, M. (2019). Resource deployment and donation allocation for epidemic outbreaks. Annals of Operations Research, 283, 9-32. [DOI:10.1007/s10479-016-2392-0]
Ross, T. J. (2009). Fuzzy logic with engineering applications. New Jerse: John Wiley & Sons. [Link]
Worldometer. (2023). COVID-19 Coronavirus Pandemic. Retrieved from: [Link]
ED-DAT. (2023). EM-DAT public. Retrieved from: [Link]