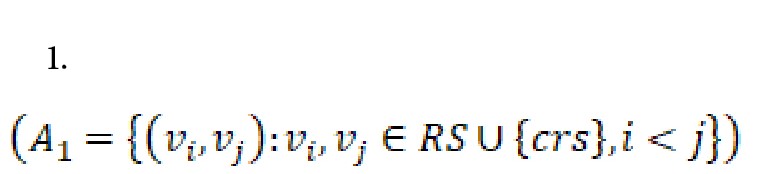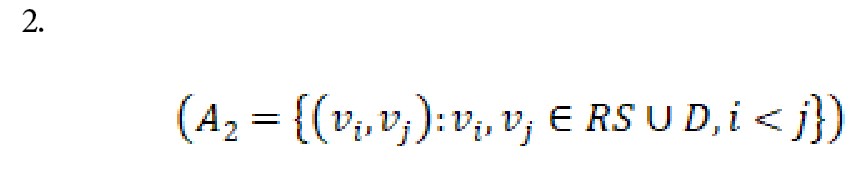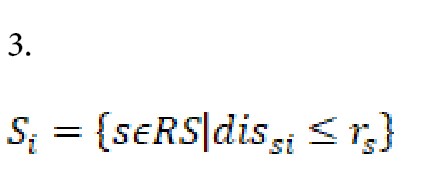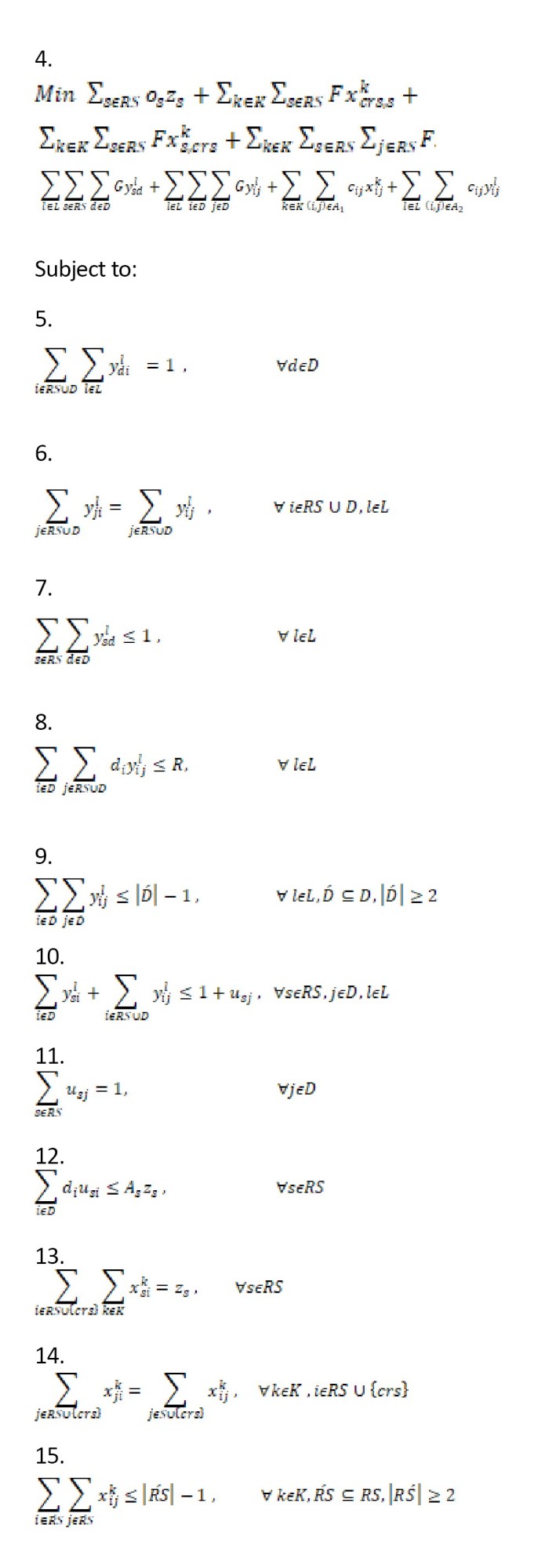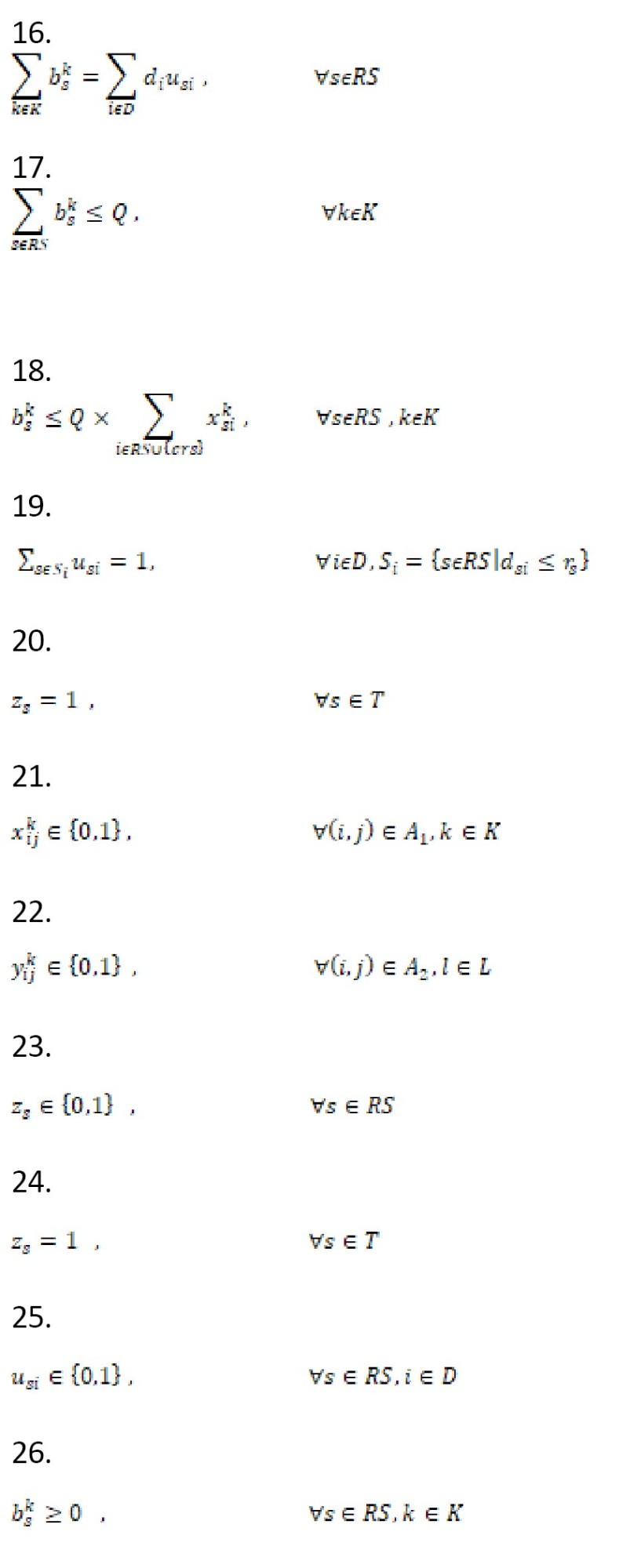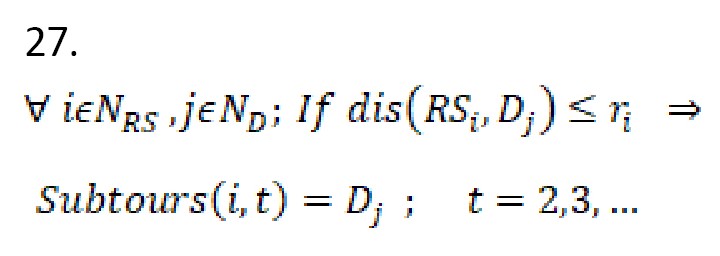مقدمه
در عصر حاضر، وقوع بلایای طبیعی نظیر زلزله، سیل و طوفان به‌عنوان یکی از بزرگ‌ترین چالش‌ها برای جوامع بشری محسوب می‌شود. با افزایش تعداد و شدت این بلایای طبیعی، بهبود و بهینه‌سازی فرایندهای امدادرسانی از اهمیت بیشتری برخوردار شده است (باتانی و همکاران (2021)؛ ژو و همکاران، 2020).  از‌این‌رو مسئله امدادرسانی در شرایط بحران، یکی از چالش‌های مهم در حوزه مدیریت بحران است. با‌توجه‌به پیچیدگی‌های موجود در این نوع مسائل، طراحی و پیاده‌سازی سیستم‌های امدادرسانی کارآمد، نیازمند رویکردهای علمی و مدل‌سازی دقیق است. تحقیقات اخیر نشان می‌دهند وجود یک مدل مسیریابی مناسب در شرایط بحرانی می‌تواند منجر به کاهش زمان واکنش و افزایش کارایی در توزیع منابع شود (مالکوف و همکاران،2022؛ ژانگ و همکاران، 2022). به علاوه، استفاده از الگوریتم‌های پیشرفته، مانند الگوریتم‌های بهینه‌سازی فراابتکاری در ترکیب با مدل‌های 2 سطحی، نویدبخش بهبودهای چشمگیری در حل مسائل پیچیده این حوزه است (پنگ و همکاران، 2023؛ لیائو و همکاران، 2020).
 مسیریابی به‌عنوان یکی از مسائل کلیدی در مدیریت بحران، به دنبال یافتن بهترین مسیر برای رسیدن به مناطق آسیب‌دیده و توزیع منابع امدادی است. در سال‌های اخیر، پژوهشگران بسیاری به این موضوع پرداخته و مدل‌های مختلفی را برای حل مسئله مسیریابی در شرایط اضطراری ارائه داده‌اند. با‌این‌حال اکثر این مدل‌ها به‌صورت تک‌‌مرحله‌ای و با تمرکز بر یک سطح از تصمیم‌گیری طراحی شده‌اند. در‌حالی‌که در واقعیت، فرایند امدادرسانی شامل تصمیم‌گیری در سطوح مختلفی، از‌جمله تخصیص منابع، تعیین مسیرهای بهینه و برنامه‌ریزی عملیات است. یکی از رویکردهای مؤثر در این زمینه، استفاده از مدل‌های مسیریابی 2 سطحی است که می‌توانند به بهینه‌سازی زمان و منابع در شرایط بحرانی کمک کنند (محمد و همکاران، 2023؛ تاراهان و همکاران، 2023). مدل‌سازی مسیریابی دو سطحی معمولاً شامل دو سطح عمده است: سطح اولیه که به شناسایی و تخصیص منابع به نقاط بحرانی می‌پردازد و سطح ثانویه که به طراحی مسیرهای بهینه برای انتقال منابع به این نقاط مربوط می‌شود (کای و همکاران، 2023). 
این رویکرد قابلیت‌های بالایی در تطبیق با تغییرات غیرمنتظره وضعیت بحران‌ها فراهم می‌کند و می‌تواند بهبود قابل‌توجهی در کارایی و سرعت امدادرسانی به همراه داشته باشد. بهبود تجربه‌های گذشته و استفاده از فناوری‌های نوین نظیر سیستم‌های اطلاعات جغرافیایی و داده‌های بزرگ می‌تواند به طراحی و اجرای مدل‌های بهینه‌تر برای مسیریابی در واکنش به بلایای طبیعی کمک کند (خانا و همکاران، 2021؛ چوئی و همکاران، 2022). 
همچنین ایجاد همکاری‌های بین‌نهادی و تبادل اطلاعات در زمان وقوع بحران‌ها، یکی دیگر از گسترش‌دهنده‌های مؤثر در بهبود فرایندهای امدادرسانی است (دالال و همکاران، 2019؛ جبور و همکاران، 2022). 
در این پژوهش، مسئله مکان‌یابی ـ مسیریابی 2 سطحی با محدودیت پوشش‌دهی بررسی می‌شود که در آن پایگاه‌های امداد تنها مجاز به ارائه خدمات در شعاع پوششی خود هستند. تصمیم‌گیری در دو سطح انجام می‌شود: در سطح اول، مکان‌یابی پایگاه‌های امداد در شهرها با در نظر گرفتن میزان آسیب‌دیدگی و امکانات موجود انجام می‌شود و در سطح دوم، تیم‌های امدادی مستقر در این پایگاه‌ها به‌صورت بهینه مسیرهایی را طی می‌کنند تا به روستاهای حادثه‌دیده در محدوده پوششی خود امدادرسانی کنند. مدل‌های پیشین معمولاً یا مکان‌یابی پایگاه‌های امداد را بدون در نظر گرفتن محدودیت پوششی بررسی کرده‌اند یا در مسیریابی تیم‌های امدادی، تأثیر سطح آسیب‌پذیری مناطق را نادیده گرفته‌اند. در این پژوهش، با ترکیب هم‌زمان این دو عامل و در نظر گرفتن یک مدل 2 سطحی، سعی شده است تا کارایی امدادرسانی در شرایط بحران بهبود یابد و با حداقل‌سازی هزینه‌ها و زمان پاسخ‌گویی، یک راهکار کارآمدتر برای مدیریت بحران ارائه شود که در آن تحلیل ریسک، ارزیابی تهدیدات و استراتژی‌های پیشگیرانه نیز لحاظ شده است.
در‌نتیجه این مقاله به ارائه یک مدل‌سازی و تحلیل مسیریابی 2 سطحی به‌صورت هم‌زمان می‌پردازد که با هدف بهینه‌سازی امداد‌رسانی در شرایط بحرانی و کاهش زمان واکنش به این بحران‌ها ارائه می‌شود. مقاله حاضر به‌صورت زیر سازماندهی شده است: 
در بخش دوم مقاله، مطالعات پیشین بررسی شده و خلأ تحقیقاتی مرتبط استخراج شده است. در بخش سوم، مسئله مسیریابی ـ مکان‌یابی تور پوششی 2 سطحی در شرایط امداد‌رسانی بیان شده و مدل ریاضی آن مطرح می‌شود. در بخش چهارم، روش حل مسئله توضیح داده شده است. بخش پنجم، شامل ساختار الگوریتم ژنتیک پیشنهادی جهت حل مسئله با پارامترهای تنظیم‌شده است. بخش ششم و هفتم مثال‌های عددی حل‌شده و تحلیل حساسیت انجام‌شده را در‌بر دارند. نهایتاً در بخش هشتم جمع‌بندی و نتیجه‌گیری ارائه شده است. 

بررسی مطالعات پیشین 
مدیرت بحران به 4 مرحله پیشگیری، آمادگی، پاسخ و بازسازی تقسیم‌بندی می‌‌شود. از میان این 4 مرحله، مرحله پاسخ، به دلیل امکان کاهش بیشتر تلفات و خسارات جانی و مالی از اهمیت ویژه‌ای برخورداراست (کانهای و همکاران، 2012). مکان‌یابی مراکز امدادرسانی و مسیریابی وسایل نقلیه امدادی جهت ارسال کالا و خدمات به آسیب‌دیدگان یکی از فعالیت‌های مرحله پاسخ است که از لحظات اولیه وقوع بحران شروع می‌‌شود و عملکرد مطلوب در مرحله پاسخ، نقش تعیین‌کننده‌­ای در کاهش تلفات و خسارات ایفا می‌کند. توجه هم‌زمان به 2 مقوله مکان‌یابی مراکز امداد و مسیریابی می‌تواند تأثیر مناسبی بر عملکرد سیستم ایفا کند. عدم توجه به مسیریابی در هنگام مکان‌یابی مراکز امدادی می‌تواند باعث افزایش زمان رسیدن اقلام امدادی به مراکز امداد شود و این امر باعث کاهش اثر‌بخشی امدادرسانی شود (جانگ و همکاران، 2009). 
استفاده از تور پوششی، رویکردی است که برخی محققین درزمینه امدادرسانی در زمان بحران به کار گرفته‌­اند. در کنار مسیریابی به روش تور پوششی، مکان‌یابی مراکز امدادرسانی و توزیع کالاهای مورد‌نیاز انجام می‌شود. در برخی تحقیقات ایجاد این مراکز به‌صورت سرپایی مطرح است تا در کمترین زمان ممکن احداث و راه­‌اندازی آن صورت گیرد. یی و ازدامار در سال 2007 به ارائه مدل مکان‌یابی و توزیع به‌منظور تخلیه مناطق آسیب‌دیده و ارائه کالاهای اساسی در شرایط بحران پرداخته‌اند. آن‌ها بسته‌­بندی مناسب کالاهای ضروری (دارو و غذا و آب آشامیدنی و غیره) به‌منظور سرعت و سهولت در توزیع را مد نظر قرار دادند و برای بسته‌های کالایی وزن‌هایی مشخص شده است که در بین آن‌ها بسته‌های دارویی از اهمیت بیشتری برخوردار است. در مدل ارائه‌شده برای مکان‌یابی مراکز امداد آن‌ها به‌صورت موقت و سرپایی در نظر گرفته شده و هزینه برپایی آن ناچیز فرض شده است. این مدل، رویکرد پوششی دارد و هدف آن کمینه کردن درصد تقاضای برآورده‌نشده است. 
برای ادبیات این تحقیق تعدادی از مطالعات مرتبط در این زمینه بررسی و نکات کلیدی آن‌ها ذکر می‌شود. مقالاتی که در آن‌ها به مسیریابی، مکان‌یابی، تور پوششی و امدادرسانی پرداخته شده است از آن جمله هستند. مفهوم پوشش کاربردهای فراوانی در دنیای واقعی دارد. به‌عنوان مثال می‌توان ترکیب مفاهیم پوشش و مسیریابی را در مسائل مرتبط با حالات اورژانسی نظیر سیل، زلزله، سونامی و غیره در مقالات (آلتای و گرین، 2006؛ دلاتوره و همکاران، 2012؛ کانهای و همکاران، 2012؛ جمالی و همکاران، 2015ب؛ جمالی و بشیری، 2020) پیدا کرد. کارنت و اسچیلینگ یکی از اولین مسائل مسیریابی به نام مسئله فروشنده پوششی  را بیان کردند که در آن ویزیت همه متقاضیان بر روی تور در نظر گرفته نشده است. آن‌ها در این مقاله به مسیریابی تیم‌های خدمات بهداشتی در کشورهای درحال‌توسعه پرداختند و برای حل مدل برنامه‌ریزی عدد صحیح خود، از یک روش ابتکاری 2 مرحله‌ای استفاده کردند. 
روش‌های حل گوناگونی برای مسئله فروشنده پوششی و انواع آن ارائه شده است که خواننده علاقه‌مند می‌تواند به مقالات مرتبط (آرکین و هاسین، 1994؛ گلدن و همکاران، 2008؛ گلدن و همکاران، 2012) مراجعه کند.
ژندریو و همکاران (ژاندر و همکاران، 1997) برای اولین‌بار با ترکیب مسائل پوشش مجموعه و فروشنده دوره‌گرد مسئله تور پوششی را تعریف کردند. آن‌ها یک مدل برنامه‌ریزی خطی ارائه دادند و سپس مسئله را با استفاده از یک روش دقیق و یک روش ابتکاری حل کردند. هاچیچا و همکاران (2000) نوعی چند‌وسیله‌ای از مسئله تور پوششی با کاربردهای گوناگون، شامل طراحی مسیرهایی برای تیم‌های ارائه‌دهنده خدمات مراقبت پزشکی سیار را گسترش دادند. در این مسئله هدف، طراحی چند تور همیلتونی بر روی یک زیرمجموعه از رئوس بود. نویسندگان یک فرموله‌سازی ریاضی و 3 الگوریتم ابتکاری را برای این مسئله ارائه کردند. 
کاربرد دیگری از پوشش برای مراقبت‌های بهداشتی در برخی مقالات ( هاجسون و همکاران، 1998؛ دورنر، فوکه و گوتجهر، 2007) ارائه شد. نولز و همکاران (2010) یک مسئله تور پوششی چند‌هدفه را پیشنهاد دادند که در آن یک ایستگاه مرکزی و مجموعه‌ای از وسایل نقلیه یکسان فرض شده بود. در این تحقیق امداد‌رسانی از‌طریق توزیع کمک‌های حیاتی مانند غذا، دارو و غیره به افراد حادثه‌دیده در یک سطح و به‌صورت غیر‌مستقیم صورت می‌گیرد. برای حل مسائل این مقاله از هر دو روش دقیق و فراابتکاری استفاده شده است. روش دقیق استفاده‌شده روش اپسیلون-محدودیت است. همچنین از روش فراابتکاری جست‌وجوی همسایگی و الگوریتم NSGA-II استفاده شده است. ناجی عظیمی و همکاران (2012) تعمیمی از مسئله تور پوششی را برای مکان‌یابی مراکز توزیع ارائه دادند. این مسئله به بررسی مکان‌یابی مراکز توزیع در جهت کمک به ارائه خدمات بشردوستانه برای همه افرادی که در یک ناحیه حادثه‌دیده قرار گرفته‌اند، می‌پردازد. در این مدل، نویسندگان وسایل حمل‌و‌نقل مختلف و با ظرفیت محدود را به کار گرفتند. برای حل این مسئله از روش ابتکاری الگوریتم شروع چندگانه (multi-start) استفاده شده است.
 نتایج محاسباتی بر روی داده‌هایی که به‌طور تصادفی تولید شده‌اند نشان می‌دهند که تنها مثال‌های کوچک با استفاده از مدل ریاضی به‌صورت کارا حل می‌شوند و روش ابتکاری پیشنهادی، مثال‌های در اندازه واقعی را با کیفیت بالا و در یک زمان منطقی حل می‌کند. الهیاری و همکاران (2014) ترکیبی از مسئله CSP و MDVRP را با نام MDCTVRP ارائه کردند. در این مقاله فرض ویزیت شدن تمامی متقاضیان وجود ندارد. تقاضای هر فرد می‌تواند به‌صورت مستقیم با ویزیت شدن در تور و یا به‌صورت غیر‌مستقیم با پوشش یافتن توسط تور برآورده شود. نویسندگان 2 فرمول‌بندی برنامه‌ریزی عدد صحیح مختلط (MIP) و 1 الگوریتم فراابتکاری هیبریدی که ترکیبی از GRASP، SA و 1 جست‌وجوی محلی تکراری است را برای این مسئله گسترش دادند. 
مطالعه‌ جمالی و بشیری (1399) که به طراحی مدلی جدید در حوزه مدیریت بحران اختصاص یافته است، در آن مسئله پوشش‌دهی مناطق بحرانی در قالب یک تور بهینه مورد بررسی قرار می‌گیرد. این مدل در شرایطی توسعه‌ یافته که محدودیت منابع و امکانات مانع از حضور مستقیم تیم‌های امدادی در تمامی نقاط آسیب‌دیده است و به همین دلیل تمرکز بر ایجاد مسیری بین برخی شهرهاست که از‌طریق آن بتوان نیاز روستاهای مجاور را نیز پوشش داد. در این چارچوب، هدف، یافتن کوتاه‌ترین مسیر همیلتونی ممکن بین مجموعه‌ای از شهرها به‌گونه‌ای است که کلیه روستاهای آسیب‌دیده نیز به‌طور غیرمستقیم تحت پوشش قرار گیرند. برای حل مدل در مقیاس‌های بزرگ، یک الگوریتم ژنتیک طراحی و پیاده‌سازی شده است. به‌منظور ارزیابی عملکرد مدل و روش پیشنهادی، چند نمونه کوچک‌مقیاس با استفاده از این الگوریتم حل شده و نتایج با خروجی‌های دقیق نرم‌افزار GAMS مقایسه شده است. بررسی‌ها نشان داده‌اند الگوریتم مذکور از‌نظر کیفیت جواب و هم‌گرایی بهینه، عملکرد مطلوبی دارد. همچنین این پژوهش به تحلیل حساسیت مدل نیز پرداخته و نشان داده است استفاده از ساختار تور پوششی در مسائل امدادرسانی می‌تواند منجر به تصمیم‌گیری‌های مؤثرتر در شرایط بحرانی شود. تمامی مقالات ارائه‌شده در‌زمینه تور پوششی، در یک سطح به مسائل می‌پردازند و این فرض وجود دارد که افراد باید خود را به تیم‌های مستقر در تور سطح اول برسانند. با این شرایط اگر افرادی دچار حادثه یا مصدوم شده باشند و نتوانند خود را به تیم‌های امداد برسانند، ممکن است جان آن‌ها در خطر باشد.  
در ادامه تعدادی از مقالات بررسی می‌شود که در حوزه حمل‌و‌نقل دو سطحی هستند. تمامی این مقالات در دو سطح بدون در نظر گرفتن مفهوم پوشش به حل مثال‌ها می‌پردازند و این فرض که ممکن است به علت آسیب ناشی از فاجعه رخ‌داده در هر شهر نتوان پایگاه امدادی با ظرفیت دلخواه برپا کرد، در نظر گرفته نشده است. یکی از اولین و مهم‌ترین مقالات در‌زمینه مسئله مسیریابی ـ مکان‌یابی دو سطحی (2E-LRP) توسط جاکوبسن و مدسن ارائه شد. جاکوبسن و مدسن در این مقاله یک کاربرد واقعی این مسئله را در ارتباط با توزیع و پخش روزنامه در بخش غربی دانمارک به کار بردند. هدف این مسئله مکان‌یابی مراکز توزیع، یافتن مسیرهای بهینه برای سطوح اول و دوم با حداقل هزینه است. نویسندگان این مقاله 3 الگوریتم ابتکاری مختلف را برای حل این مسئله ارائه کردند (جاکوبسن و مدسن, 1980). مدسن (1983) با انجام اصلاحاتی بر روی 2 الگوریتم از 3 الگوریتم ابتکاری بیان‌‌شده در قبل، کارایی آن‌ها را افزایش داد و برای همان مسئله از آن‌ها استفاده کرد. بوسیا و همکاران (2101) یک روش حل فراابتکاری جست‌وجوی ممنوع (TS) را برای مسئله مسیریابی ـ مکان‌یابی 2 سطحی با ظرفیت محدود ارائه کردند. این روش در اصل برای مسائل LRP طراحی شده بود و قبلاً توسط ناگی و صالحی (1996) و توزان و بورکه (1999) پیشنهاد شده بود. ایده اصلی این الگوریتم، اولاً تجزیه مسئله اصلی به 2 مسئله LRP و ثانیاً تجزیه هر LRP به یک مسئله مکان‌یابی تسهیلات دارای ظرفیت و یک مسئله مسیریابی وسایل حمل‌و‌نقل چند‌ایستگاهی بود. بنابراین الگوریتم TS ارائه‌شده شامل 2 مرحله اصلی است: مرحله اول مکان‌یابی است که در آن تعداد و مکان تسهیلات مشخص می‌شوند و مرحله دوم مسیریابی است. یک رویکرد از پایین به بالا در این مقاله استفاده شده است، به این‌ صورت که در ابتدا یک راه‌حل برای سطح دوم ساخته می‌شود و سپس با‌توجه‌به آن راه‌حل، راه‌حل سطح اول ساخته می‌شود. در تحقیقی مشابه، کرانیک و همکاران (الف2011) نیز از همین ایده برای حل مسئله خود استفاده کردند. 
ذگردی و نیکبخش (2010) 1 مدل ریاضی 4 اندیسه، 1 روش ابتکاری سریع و کارا و 1 کران پایین را برای مسئله 2E-LRP با محدودیت‌های پنجره‌های زمانی نرم ارائه دادند. 
روش ابتکاری پیشنهاد‌شده تلاش می‌کند مسئله را با استفاده از ایجاد یک راه‌حل اولیه، سپس بهبود دادن آن از‌طریق جست‌وجوی 6 همسایه از راه‌حل اولیه و استفاده از روش ابتکاری Or-opt حل کند. در پایان، نتایج محاسباتی نشان از کارایی روش ابتکاری پیشنهاد‌شده و استفاده از کران پایین ارائه‌شده دارد. 
کرانیک و همکاران (2011 ب) 3 مدل‌سازی بر پایه برنامه‌ریزی خطی عدد صحیح مختلط برای مسئله مسیریابی ـ مکان‌یابی 2 سطحی با ظرفیت محدود معرفی کردند. هدف این مقاله معرفی مسئله 2E-LRP و به دست آوردن این بینش است که این مسئله باتوجهبه مدل‌های ارائه‌شده، برای مثال‌های گوناگون چگونه عمل می‌کند.
 محاسباتی برای مثال‌های با اندازه متوسط و کوچک برای مدل‌های 2 شاخصه و 3 شاخصه انجام گرفت. این مثال‌ها با استفاده از حل‌کننده XPRESS حل شدند و سپس از‌نظر زمان محاسباتی، کران‌ها و کیفیت راه‌حل‌ها با هم مقایسه شدند. نتایج محاسباتی نشان دادند مدل 3 شاخصه کران‌های پایین بهتری به دست می‌دهد و کاراتر از مدل 2 شاخصه برای حل مثال‌های با اندازه متوسط است. 
کونتاردو و همکاران (2012) الگوریتم شاخه و برش‌ را که یک روش دقیق است برای حل مسئله 2E-LRP پیشنهاد دادند. در این مقاله نویسندگان یک مدل‌سازی جریان مبنا را پیشنهاد دادند که بر‌اساس الگوریتم شاخه و برش طراحی شده و قادر است مثال‌های در اندازه کوچک و متوسط را به‌صورت بهینه در یک زمان محاسباتی منطقی حل کند. این فرموله‌بندی ریاضی یک مدل برنامه‌ریزی خطی عدد صحیح مختلط است که توسط چندین نامساوی معتبر که از مقالات بلنگور و همکاران (2011) و کونتاردو و همکاران (2013) گرفته شده، تقویت شده است. همچنین نویسندگان یک الگوریتم ALNS را برای حل این مسئله پیشنهاد دادند. هر دو الگوریتم دقیق و فراابتکاری ارائهشده بر‌اساس تجزیه مسئله 2E-CLRP به 2 مسئله LRP در هر سطح طراحی شده‌اند. این کار نویسندگان را قادر می‌کند الگوریتم‌های پیشنهاد‌شده را برای مسئله CLRP در هر سطح به کار گیرند و سپس راه‌حل‌های جزئی به‌دست‌آمده را برای به دست آوردن یک راه‌حل کلی ترکیب کنند. نتایج محاسباتی که بر روی یک مجموعه بزرگ از مثال‌ها انجام گرفت حاکی از آن است که الگوریتم ALNS کاراتر از روش‌های ابتکاری موجود است. علاوه‌براین روش شاخه و برش ارائه‌شده، کران‌های پایین دقیقی را فراهم می‌آورد. 
نگوین و همکاران (2012 الف) نوعی از مسئله مسیریابی ـ مکان‌یابی 2 سطحی با ظرفیت محدود و دارای یک ایستگاه که در آن تنها یک ایستگاه با مکان مشخص وجود دارد را بررسی کردند. آن‌ها این مسئله را با یک مدل برنامه‌ریزی خطی عدد صحیح و با استفاده از متغیرهای تصمیم 2 شاخصه مدل‌سازی کردند. همچنین آن‌ها 4 روش ابتکاری سازنده، یک روش فراابتکاری ترکیبی GRASP که با استفاده از learning process و path relinking تقویت شده است را برای حل این مسئله ارائه کردند. الگوریتم GRASP از 3 روش ابتکاری تصادفی حریصانه برای تولید راه‌حل‌های آزمایشی و 2 روش VND برای بهبود آن‌ها استفاده می‌کند. نویسندگان این مقاله 2 مجموعه مثال را برای این مسئله تعریف کردند که شامل حداکثر 10 مرکز توزیع و 200 متقاضی بودند. نتایج محاسباتی نشان دادند الگوریتم GRASP ترکیبی مذکور کاراتر از دیگر روش‌های ابتکاری بیان‌شده در این مقاله هستند (نگوین و همکاران (2012 ب). یک مدل برنامه‌ریزی خطی عدد صحیح مختلط جدید و یک الگوریتم جست‌وجوی محلی تکراری چند شروعی را برای 2E-CLRPSD پیشنهاد دادند که دارای چند ویژگی خاص است. این ویژگی‌ها شامل موارد زیر هستند: 
اولین ویژگی یک معیار پذیرش برای راه‌حل‌ها است. بهطوری‌که این راه‌حل‌ها تنها در صورتی می‌توانند پذیرفته شوند که اختلافشان از بهترین راه‌حل شناخته‌شده از یک مقدار معین تجاوز نکند. دومین ویژگی شامل 2 روش بهبود‌یافته بر پایه جست‌وجوی 2 همسایه با پیچیدگی متفاوت است و سومین ویژگی شامل یک لیست است که راه‌حل‌های بازدید‌شده اخیر توسط یک الگوریتم TS را ذخیره می‌کند. در ادامه نتایج الگوریتم ILS چند‌شروعی با روش path relinking تقویت شد. این الگوریتم همراه با تعدای روش ابتکاری ساده‌تر و با کارایی کمتر بر روی تعدادی از مثال‌های پایه که در مقاله (نگوین و همکاران، 2012الف) تولید شده بودند، مورد آزمایش قرار گرفت. همچنین در این مقاله، نویسندگان تنها بهترین مقادیر به‌دست‌آمده از تعدادی اجرا را گزارش داده‌اند. در‌حالی‌که هیچ اطلاعاتی در‌مورد میانگین عملکرد اجراها داده نشده است. مقایسه دو مقاله (نگوین و همکاران، 2012الف؛ نگوین و همکاران، 2012ب) نشان می‌دهد که ILS چند‌شروعی ترکیب شده با path relinking در مقاله (نگوین و همکاران، 2012ب)کمی بهتر از الگوریتم GRASP ترکیب شده با learning process و path relinking بیان‌شده در مقاله (نگوین و همکاران، 2012 الف) است. اسچونگر و همکاران (2012) روش ابتکاری جست‌وجوی همسایگی متغیر را برای 2E-CLRP گسترش دادند که این الگوریتم قبلاً توسط پیرکویسر و رایدل (2010) برای مسئله LRP طراحی شده بود. 
محاسبات بر روی 3 مجموعه از مثال‌های به‌کار‌رفته توسط کونتاردو و همکاران (2013) در مقاله انجام گرفت؛ کارایی الگوریتم VNS در مقایسه با کارایی الگوریتم آزمون‌شده در مقالات (کانتاردو و همکاران، 2013؛ نگوین و همکاران، 2012الف؛ نگوین و همکاران، 012ب) مورد تأیید قرار گرفت. نتایج محاسباتی نشان دادند الگوریتم VNS پیشنهاد‌شده بهتر از روش‌های فراابتکاری پیشنهاد‌شده در (نگوین و همکاران، 2012الف؛ نگوین و همکاران، 2012ب) هستند، اما به‌طور متوسط الگوریتم ALNS ارائه‌شده در (کانتاردو و همکاران، 2013) عملکرد بهتری داشته است. گویندان و همکاران یک مدل بهینه‌سازی چند‌هدفه را برای یک شبکه زنجیره تأمین مواد غذایی فاسد‌شدنی پیشنهاد دادند. این مدل یک مسئله مسیریابی ـ مکان‌یابی 2 سطحی با پنجره‌های زمانی برای طراحی یک شبکه زنجیره تأمین و بهینه‌سازی اهداف محیطی و اقتصادی در یک شبکه زنجیره تأمین مواد غذایی فاسد‌شدنی را تعریف می‌کند. هدف این مدل، شناسایی تعداد و مکان تسهیلات، بهینه‌سازی مقدار مواد حمل‌شده به سطوح پایین و مسیریابی در هر سطح است. همچنین هدف دیگر این مقاله کاهش هزینه‌های مرتبط با کربن ناشی از تماس لاستیک‌های وسایل نقلیه با سطح جاده و انتشار گازهای گلخانه‌ای در کل شبکه است. روش پیشنهاد‌شده شامل یک رویکرد هیبریدی چندهدفه جدید به نام فراابتکاری هیبریدی مبتنی بر جمعیت برای چندهدفه (MHPV)، ترکیبی از 2 الگوریتم چند‌هدفه شناخته‌شده به نام الگوریتم بهینه‌سازی تجمع ذرات چند‌هدفه و الگوریتم جست‌وجوی همسایگی متغیر چند‌هدفه تعدیل‌شده است. نتایج نشان می‌دهند این رویکرد هیبریدی راه‌حل‌های بهتری در مقایسه با روش‌های دیگر ارائه می‌دهد. 
جمالی و همکاران (1394) در مقاله‌ای به بررسی و حل مسئله امدادرسانی 2 سطحی نقاط آسیب‌دیده از بحران پرداختند. این مقاله به بررسی مسئله مسیریابی ـ مکان‌یابی 2 سطحی ظرفیت‌دار با پنجره‌های زمانی سخت در شرایط امدادرسانی برای افرادی که در یک ناحیه بحران‌زده قرار گرفته‌اند، می‌پردازد. در این شرایط افراد باید در اسرع وقت توسط تیم‌های امدادرسان مورد حمایت قرار گیرند و لازمه این امر، یافتن مسیرهای بهینه جهت حمل‌و‌نقل سریع این تیم‌ها و ارائه کالاهای ضروری مورد‌نیاز به افراد حادثه‌دیده است. هدف این مقاله تعیین مجموعه‌ای بهینه از پایگاه‌های امداد جهت استقرار تیم‌های امداد‌رسان، مسیریابی بهینه این تیم‌ها از پایگاه اصلی به پایگاه‌های امداد برپا‌شده و سپس از این پایگاه‌ها به نقاط حادثه‌دیده است. به‌طوری‌که کل تقاضا برآورده شود و هزینه کل که شامل مجموع هزینه برپا شدن پایگاه‌های امداد و هزینه‌های حمل‌و‌نقل هستند، حداقل شود. نتایج حاصل از حل مسئله نشان می‌دهند الگوریتم ژنتیک پیشنهادی، الگوریتمی کارا و کاربردی است. این مسئله با مسائل مسیریابی ـ مکان‌یابی 1 سطحی و تور پوششی در شرایط امداد‌رسانی طی چندین مثال و در شرایط یکسان مقایسه و نتیجه‌گیری شد این مسئله به مراتب دارای هزینه کمتری بوده و بنابراین کاراتر است. در ادامه به تحلیل حساسیت مسئله از‌نظر ظرفیت وسایل حمل‌و‌نقل، ظرفیت پایگاه‌های امداد و تعداد این پایگاه‌ها پرداخته و نتیجه‌گیری شد با کاهش ظرفیت وسایل حمل‌و‌نقل سطح دوم، مسئله امداد‌رسانی 2 سطحی به مسئله تور پوششی هم‌گرا می‌شود، همچنین با افزایش ظرفیت پایگاه‌های امداد و استفاده از وسایل حمل‌و‌نقل بزرگ‌تر، این مسئله به مسئله مسیریابی ـ مکان‌یابی 1 سطحی هم‌گرا می‌شود و نهایتاً با برپایی پایگاه‌های امداد با ظرفیت بیشتر و استفاده از وسایل حمل‌و‌نقل متناظر با آن‌ها، امداد‌رسانی با هزینه کمتر و سرعت بیشتری انجام خواهد گرفت.
 اولیواری و همکاران (2025) مسئله تور پوشش چند وسیله نقلیه را تعریف می‌کنند. هدف تعیین مجموعه‌ای از مسیرها با حداقل هزینه است که محدودیت‌های زیر را برطرف می‌کند: 
هر مسیر در انبار شروع و به پایان می‌رسد. هر تسهیلات اجباری دقیقاً 1 بار در یک مسیر واحد بازدید می‌شود. هر مسیر از امکانات p بیشتر بازدید نمی‌کند و حداکثر هزینه آن q است. برای هر مشتری، حداقل یک تسهیلات اختیاری از مجموعه پوشش آن باید توسط یکی از مسیرها بازدید شود. در این مقاله، یک الگوریتم دقیق شاخه ـ برش و قیمت. خانواده جدیدی از برش‌های ظرفیت مانند و مجموعه جدیدی از نمونه‌های معیار وجود دارد. نتایج نشان داد الگوریتم پیشنهادی از بهترین روش دقیق از ادبیات عملکرد بهتری دارد و برش‌های پیشنهادی عملکرد آن را با یک مرتبه قدر بهبود می‌بخشد. 
در ادامه چند مقاله در‌زمینه امداد‌رسانی بحران که مرتبط با این تحقیق هستند بررسی و ویژگی‌های آن‌ها به‌طور خلاصه ذکر می‌شوند. 
راس و گوتجهر (2014) یک مدل بهینه سازی 3 هدفه را برای یک مسئله مسیریابی ـ مکان‌یابی انبار جهت امداد‌رسانی بعد از وقوع حادثه پیشنهاد دادند. در این مسئله چند ایستگاه وجود دارد که باید در ابتدا مکان‌یابی شوند. سپس باید متقاضیان به این ایستگاه‌ها تخصیص یابند و در ادامه مسیریابی به این متقاضیان توسط یک ناوگان از وسایل حمل‌و‌نقل با ظرفیت یکسان انجام گیرد. تعداد، اندازه و مکان انبارها، تخصیص متقاضیان به انبارها و مسیریابی حمل کالاها باید به‌گونه‌ای انجام گیرد که حداقل هزینه را در‌بر داشته باشد. نویسندگان برای حل این مسئله از روش دقیق اپسیلون-محدودیت و الگوریتم VNS استفاده کرده‌اند. وانگ و همکاران یک مدل مسیریابی ـ مکان‌یابی عدد صحیح غیرخطی را برای مسئله توزیع امداد 1‌ سطحی با در نظر گرفتن مدت‌زمان پیموده‌شده، کل هزینه و قابلیت اطمینان تعریف کردند. به‌طوری‌که در این مدل شکست تقاضا مجاز است. به این معنی که وسایل حمل‌و‌نقل می‌توانند در آخرین نقطه توقفشان تا فرا‌رسیدن مأموریت بعدی منتظر بمانند بدون اینکه به ایستگاه برگردند. توزیع امداد شامل مکان‌یابی مراکز توزیع، مسیریابی وسایل نقلیه و زمان‌بندی پس از وقوع زلزله است. در این مسئله از یک ناوگان وسایل حمل‌و‌نقل ناهمگون که دارای ظرفیت و سرعت‌های متفاوت هستند استفاده شده است. هدف این مسئله مشخص کردن یک زیر‌مجموعه از مراکز توزیع جهت بازگشایی، تخصیص نواحی بحران‌زده و وسایل حمل‌و‌نقل به مراکز توزیع و برنامه‌ریزی مسیرها مراکز توزیع به نواحی حادثه‌دیده با‌توجه‌به ظرفیت وسایل حمل‌و‌نقل و مجاز بودن شکست تقاضا است. نویسندگان این مقاله از 2 روش فراابتکاری الگوریتم ژنتیک مرتب‌سازی نامغلوب نسخه2 (NSGA-II و NSDA) برای حل مدلشان استفاده کردند. این 2 روش در عملگرهای تقاطع و جهش با هم تفاوت دارند. برای ارزیابی کارایی 2 روش پیشنهاد‌شده، 5 مجموعه از مثال‌ها در اندازه‌های مختلف به‌صورت تصادفی تولید و توسط مدل‌های پیشنهادی حل شد. مقایسه جواب‌ها نشان داد روش NSGA-II در اکثر موارد نسبت به روش NSDA عملکرد بهتری داشته است. 
وانگ و ژانگ (2005) برای بهینه‌سازی مکان مراکز امداد مدلی را بر‌اساس احتمال وقوع فاجعه، توابع هدف پراکندگی فاجعه و امداد‌رسانی ارائه کردند. آن‌ها یک الگوریتم ژنتیک (GA) را با استفاده از کدهای باینری و در نظر گرفتن یک روش ابتکاری حریصانه برای محاسبه تابع هدف گسترش دادند. نتایج محاسباتی که برروی مثال‌ها انجام گرفت نشان داد الگوریتم مذکور دارای عملکرد رضایت‌بخشی است. هان و ژانگ (2009) یک مسئله مکان‌یابی تسهیلات اورژانسی را گسترش دادند که به‌عنوان یک مسئله برنامه‌ریزی خطی مدل‌سازی شد. آن‌ها یک الگوریتم ژنتیک (GA) که در آن هر کروموزوم از شماره سریال تسهیلات اورژانسی موردنظر تشکیل شده بود و تنوع جمعیت به واسطه استفاده از یک عملگر احتمالی جهش پشتیبانی می‌شد را ارائه کردند. نتایج آزمایشات نشان دادند کارایی الگوریتم ژنتیک ارائه‌شده بسیار بیشتر از کارایی الگوریتم‌های دیگر است. 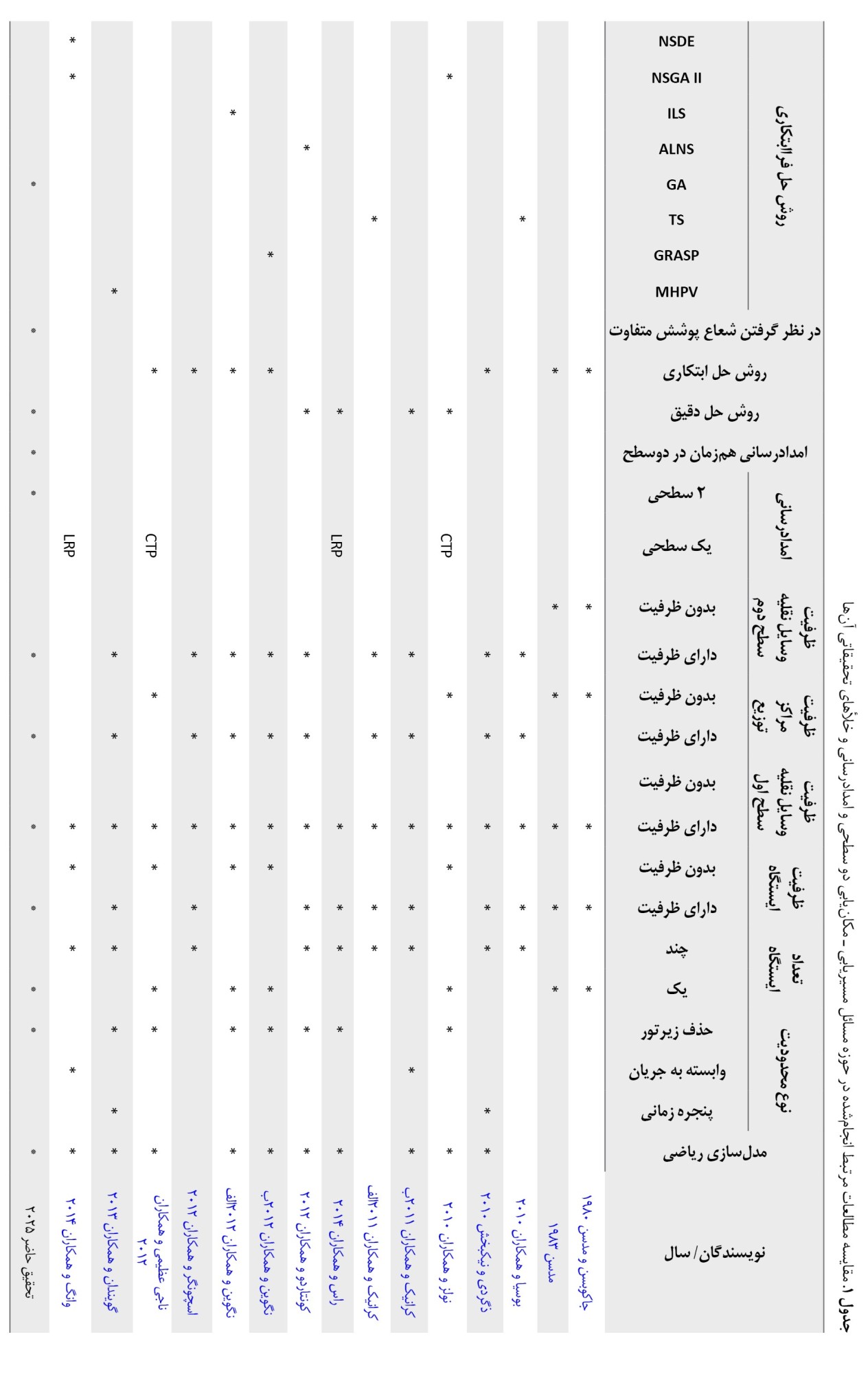جدول شماره 1 به‌طور خلاصه، ویژگی‌های مطالعات انجام‌شده در حوزه مسائل تور پوششی، مسیریابی ـ مکان‌یابی دو سطحی و امداد‌رسانی را به همراه خلأهای تحقیقاتی نشان می‌دهد. 


هدف پاشاپور و همکاران (2024) کمک به سازمان‌های بشردوستانه در بهینه‌سازی مقرون‌به‌صرفه لجستیک امکانات سیار با ظرفیت مورد‌استفاده برای ارائه کمک‌های امدادی به پناهندگان در حال عبور در یک محیط چند دوره بود. 1 مدل برنامه‌ریزی خطی عدد صحیح مختلط فرموله شد و 2 روش راه‌حل برای حل این مشکل پیچیده پیشنهاد شد: یک رویکرد تجزیه سریع بندرز به‌عنوان یک روش حل دقیق و یک الگوریتم ریاضی که بر یک دستور کار اصلاح و بهینه‌سازی پیشرفته تأکید دارد.
با مشاهده جدول شماره 1، واضح است مدل‌سازی مسئله تور پوششی 2 سطحی در شرایط امدادرسانی، امداد‌رسانی در دو سطح و به‌صورت هم‌زمان به نقاط حادثه‌دیده، در نظر گرفتن شعاع پوششی متفاوت با‌توجه‌به امکانات موجود در پایگاه‌ها، طراحی الگوریتم فراابتکاری ژنتیک برای حل این مسئله در اندازه‌های واقعی و در نظر گرفتن چند وسیله نقلیه در سطح اول و دوم در صورت لزوم از نکاتی هستند که تاکنون مورد مطالعه قرار نگرفته‌اند. 

بیان مسئله و مدل‌سازی ریاضی آن
فرض کنید مجموعه معینی از رئوس وجود دارند که باید در تور قرار گیرند. همچنین رئوسی موجودند که می‌توانند جهت بازدید در تور قرار گیرند. مجموعه سومی از رئوس نیز موجودند که باید حداقل به‌وسیله یک شهر ویزیت شده، پوشش یابند. منظور از پوشش این است که این رئوس باید در یک فاصله از پیش تعیین‌شده نسبت به شهر ویزیت‌شده‌ای در تور قرار گیرند. حال اگر در یک منطقه جغرافیایی، حادثه‌ای طبیعی نظیر سیل، زلزله و غیره رخ داده باشد و هدف امداد‌رسانی به افراد حادثه‌دیده با استفاده از مسئله تور پوششی کلاسیک باشد، افراد حادثه‌دیده باید خود را به نقاط ویزیت‌شده جهت دریافت خدمات برسانند. در این شرایط ممکن است به هر علتی، مثلاً محدودیت زمانی، دوری راه، آسیب‌دیدگی افراد حادثه‌دیده و غیره، تعدادی از افراد حادثه‌دیده نتوانند خود را به پایگاه‌های امداد برپا‌شده در تور اصلی برسانند و خدمت مورد‌نظرشان را دریافت کنند و قطعاً در این حالت جان انسان‌های زیادی ممکن است در خطر باشد. 
زمانی که ظرفیت پایگاه‌ها حداکثر برابر با مقدار تقاضای کل افراد حادثه‌دیده باشد، افزایش ظرفیت پایگاه‌ها مجاز است و میتوان در آن پایگاه‌ها از وسایل حمل‌ونقل متناظر با ظرفیت آن پایگاه‌ها بهره برد و در این صورت امدادرسانی با هزینه کمتر و سرعت بیشتری انجام خواهد گرفت، ولی اگر با یک برنامه‌ریزی نادرست، پایگاه‌های امداد با ظرفیت بیشتر از حد نیاز برپا شوند، با آنکه این کار هزینه امدادرسانی بیشتری در‌بر دارد، در سرعت امدادرسانی تأثیر چندانی نمی‌گذارد؛ بنابراین پایگاه‌های امداد باید با ظرفیت بهینه و متناسب با میزان تقاضای افراد حادثه‌دیده برپا گردند (جمالی و همکاران، 2015 الف). 
از‌آنجایی‌که یکی از اهداف اصلی امداد‌رسانی، کاهش مرگ‌ومیر افراد حادثه‌دیده است، نمی‌توان در چنین شرایطی انتظار داشت مردم بحران‌زده، خود را به تیم‌های امداد که در پایگاه‌های شهری مستقر شده‌اند، جهت دریافت خدمت برسانند. بنابراین استفاده از تور سطح دوم برای امدادرسانی مستقیم به افراد حادثه‌دیده لازم به نظر می‌رسد. برای درک بهتر مسئله فرض کنید در یک منطقه جغرافیایی، تعدادی شهر و روستا وجود دارد که در شرایط بحرانی بعد از وقوع حادثه قرار دارند. شهرها به 2 دسته تقسیم می‌شوند: دسته اول شامل شهرهایی هستند که حادثه دیده‌اند و باید حتماً در تور سطح اول قرار گیرند و در ضمن باید در آن‌ها پایگاه‌های امداد جهت خدمت‌رسانی به روستاهای حادثه‌دیده برپا شود. 
دسته دوم شامل شهرهایی ‌هستند که حادثه ندیده‌اند و می‌توانند در تور سطح اول به‌عنوان پایگاه امداد‌رسانی جهت امداد‌رسانی به نقاط حادثه‌دیده قرار گیرند. همه پایگاه‌های امداد دارای ظرفیت محدود و هزینه بازگشایی هستند. 
امداد‌رسانی در سطح دوم با‌توجهبه امکانات آن سطح، صرفاً به نقاط آسیب دیده‌ای امکان‌پذیر است که در فاصله کمتری از یک شعاع معین نسبت به پایگاه امداد متناظر قرار داشته باشند. در این مقاله امداد‌رسانی از پایگاه مرکزی به شهرها و سپس از شهرها به روستاهای حادثه‌دیده در دو سطح و به‌صورت هم‌زمان انجام می‌گیرد. به این صورت که در سطح اول پایگاه‌های امداد شهری برپا و تجهیز می‌شوند، به محض تجهیز شدن این پایگاه‌ها، امداد‌رسانی از آن‌ها به روستاهای حادثه‌دیده‌ای که تحت پوشش آن‌ها هستند و به آن‌ها تخصیص یافته‌اند توسط وسایل نقلیه امدادی مستقر در آن‌ها صورت می‌گیرد. این کار باعث می‌شود که تورها به‌طور هم‌زمان در دو سطح تشکیل شوند و امداد‌رسانی با سرعت بیشتری انجام گیرد. 
پایگاه مرکزی موجود در این مسئله دارای امکاناتی نظیر وسایل حمل‌و‌نقل جهت امدادرسانی و مواد مورد‌نیاز افراد حادثه‌دیده است. فاصله پوششی شهرها با یکدیگر متفاوت است و هر شهر فقط می‌تواند به روستاهایی که در فاصله پوششی آن شهر قرار دارند، امداد‌رسانی کند. هدف این مقاله تعیین مجموعه‌ای بهینه از پایگاه‌های امداد جهت استقرار تیم‌های امدادرسان و تجهیز آن‌ها توسط پایگاه امداد مرکزی، مسیریابی بهینه این تیم‌ها از پایگاه مرکزی به پایگاه‌های امداد برپا‌شده و سپس از این پایگاه‌ها به روستاهای حادثه‌دیده است. به‌طوری‌که نیاز امداد تمامی نقاط حادثه‌دیده برآورده شود و هزینه کل که شامل مجموع هزینه برپا شدن پایگاه‌های امداد و هزینه‌های حمل‌و‌نقل هستند، حداقل شود.
 این مسئله دارای دو سطح است: سطح اول شامل پایگاه اصلی و پایگاه‌های امداد برپا‌شده و سطح دوم شامل این پایگاه‌ها و نقاط حادثه‌دیده است. در هر سطح، یک ناوگان از وسایل نقلیه مشابه با ظرفیت‌های یکسان و معین وجود دارد. وسایل حمل‌ونقل سطح اول در پایگاه اصلی موجودند. هر وسیله نقلیه سطح اولی یک زیر‌مجموعه از پایگاه‌های امداد را می‌پیماید و سپس به پایگاه مرکزی برمی‌گردد. به محض رسیدن وسیله نقلیه سطح اول به پایگاه‌های امداد و تأمین شدن مقدار تقاضای تخصیص‌یافته به آن پایگاه، وسیله نقلیه سطح دوم از آن پایگاه حرکت خود را آغاز می‌کند. مسیری را که برای ارائه خدمت و توزیع مواد امدادی به افراد حادثه‌دیده در نظر گرفته شده است را می‌پیماید و سپس به همان پایگاه بر می‌گردد. در این مسئله وسایل نقلیه سطح اول ظرفیت بیشتری نسبت به وسایل نقلیه سطح دوم دارند. هر پایگاه امداد برپا‌شده باید دقیقاً توسط یک وسیله نقلیه سطح اول بازدید شود. به‌طور مشابه هر نقطه متقاضی دریافت خدمات امداد باید دقیقاً توسط یک وسیله نقلیه سطح دوم خدمت‌رسانی شود. بنابراین باید مقدار تقاضای امدادی هر نقطه حادثه‌دیده، کوچک‌تر از ظرفیت هر‌یک از وسایل نقلیه سطح دوم باشد. 
با‌توجه‌به توضیحات بیان‌شده می‌توان نتیجه گرفت مسئله مورد‌بررسی در این تحقیق، تعمیمی از مسائل تور پوششی و مسئله مسیریابی-مکان‌یابی 2 سطحی در شرایط امداد‌رسانی است به همین علت این مسئله با عنوان مسئله مسیریابی ـ مکان‌یابی تور پوششی 2 سطحی در شرایط امدادرسانی نام‌گذاری می‌شود که به‌اختصار در این مقاله مسئله تور پوششی دو سطحی نامیده می‌شود. نوآوری‌های تحقیق حاضر را می‌توان در موارد زیر دانست: 
مدل‌سازی مسئله تور پوششی دو سطحی در شرایط امدادرسانی، امدادرسانی در دو سطح و به‌صورت هم‌زمان به نقاط حادثه‌دیده، در نظر گرفتن شعاع پوششی متفاوت با‌توجه‌به امکانات موجود در پایگاه‌ها، طراحی الگوریتم فراابتکاری ژنتیک برای حل این مسئله در اندازه‌های واقعی و تحلیل حساسیت آن. 
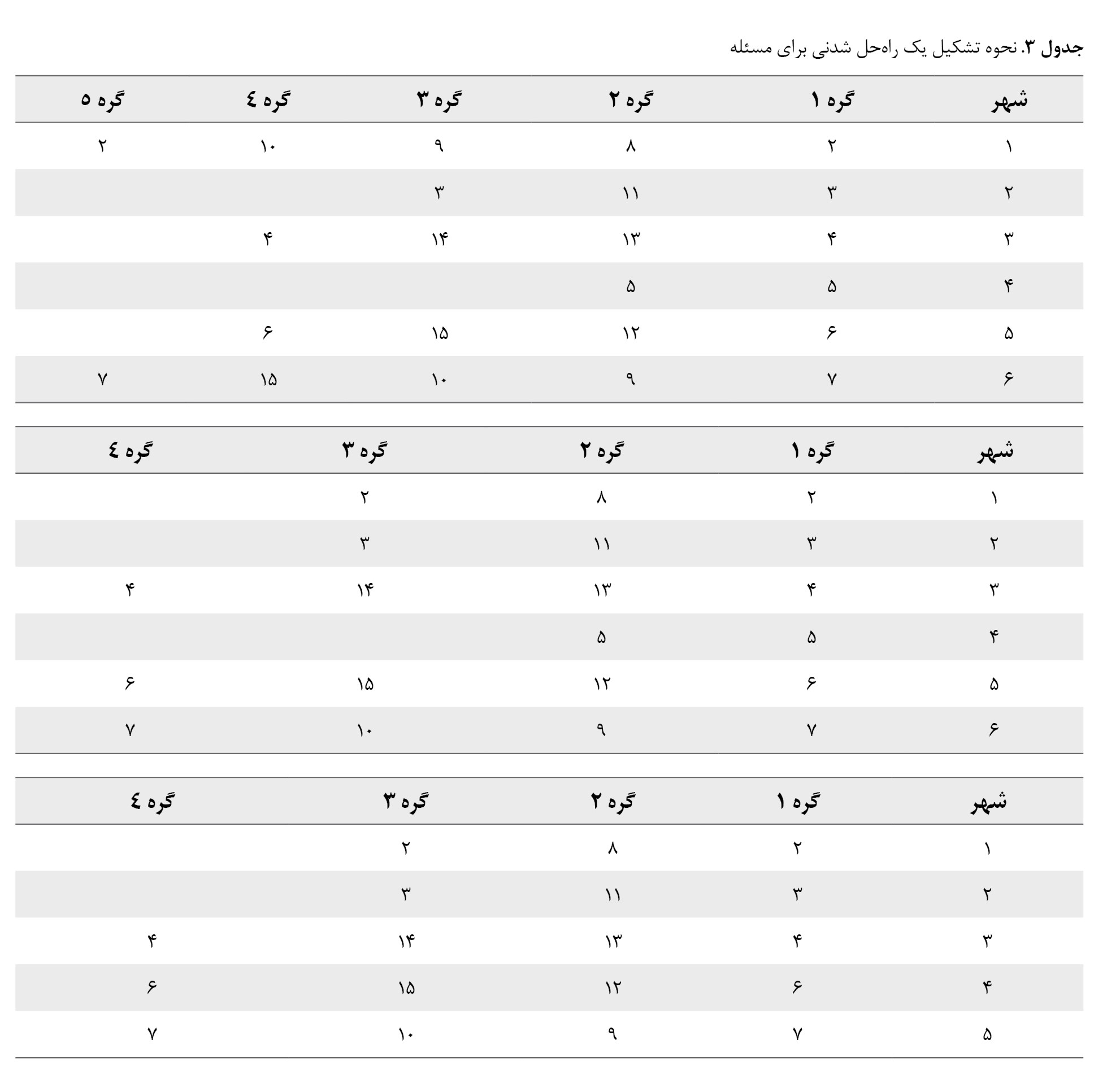
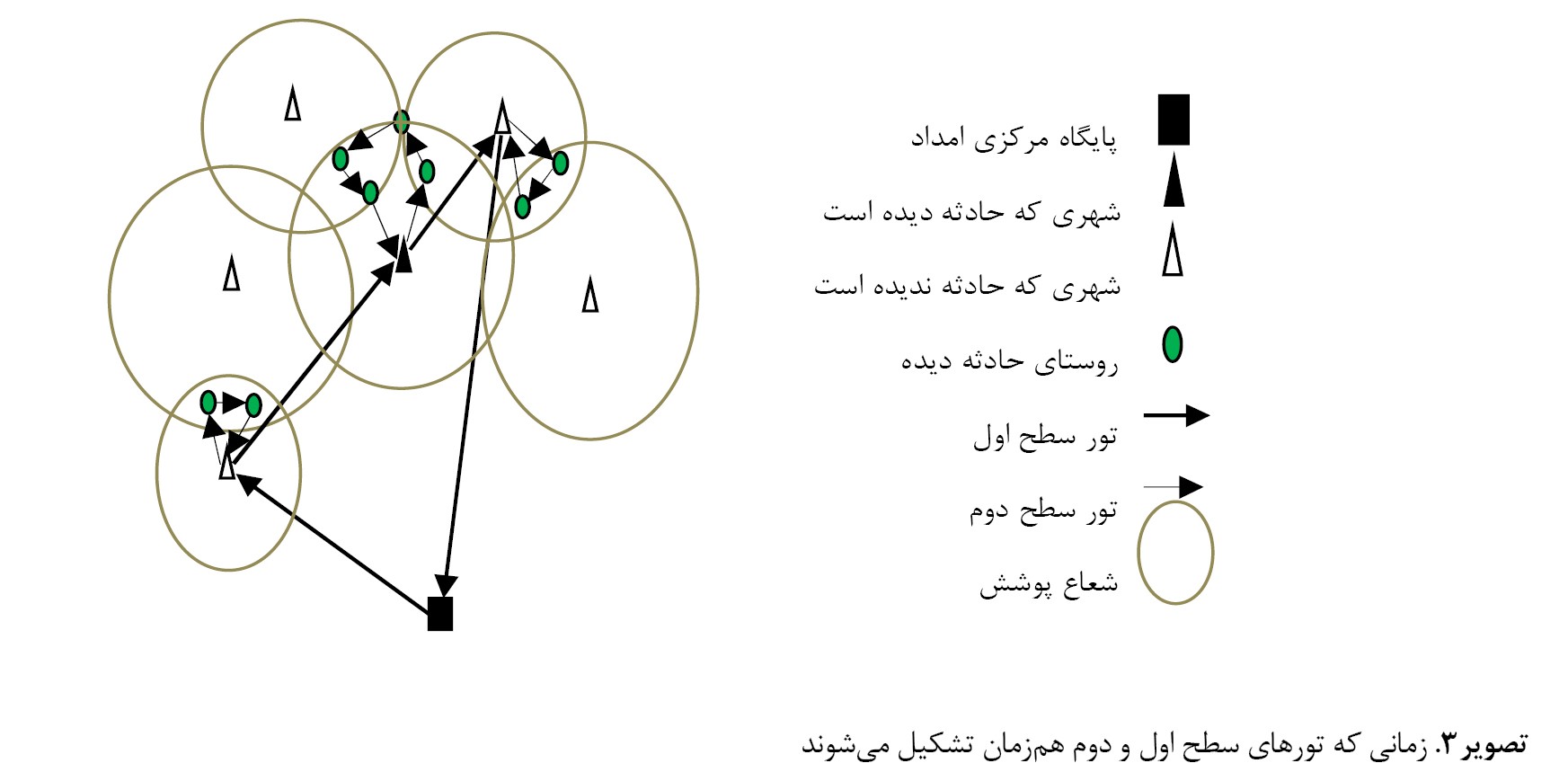
تصویر شماره 1 راه‌حلی شدنی را برای یک مثال (مثال 4 جدول شماره 7) از مسئله مورد‌بررسی در این تحقیق نشان می‌دهد.

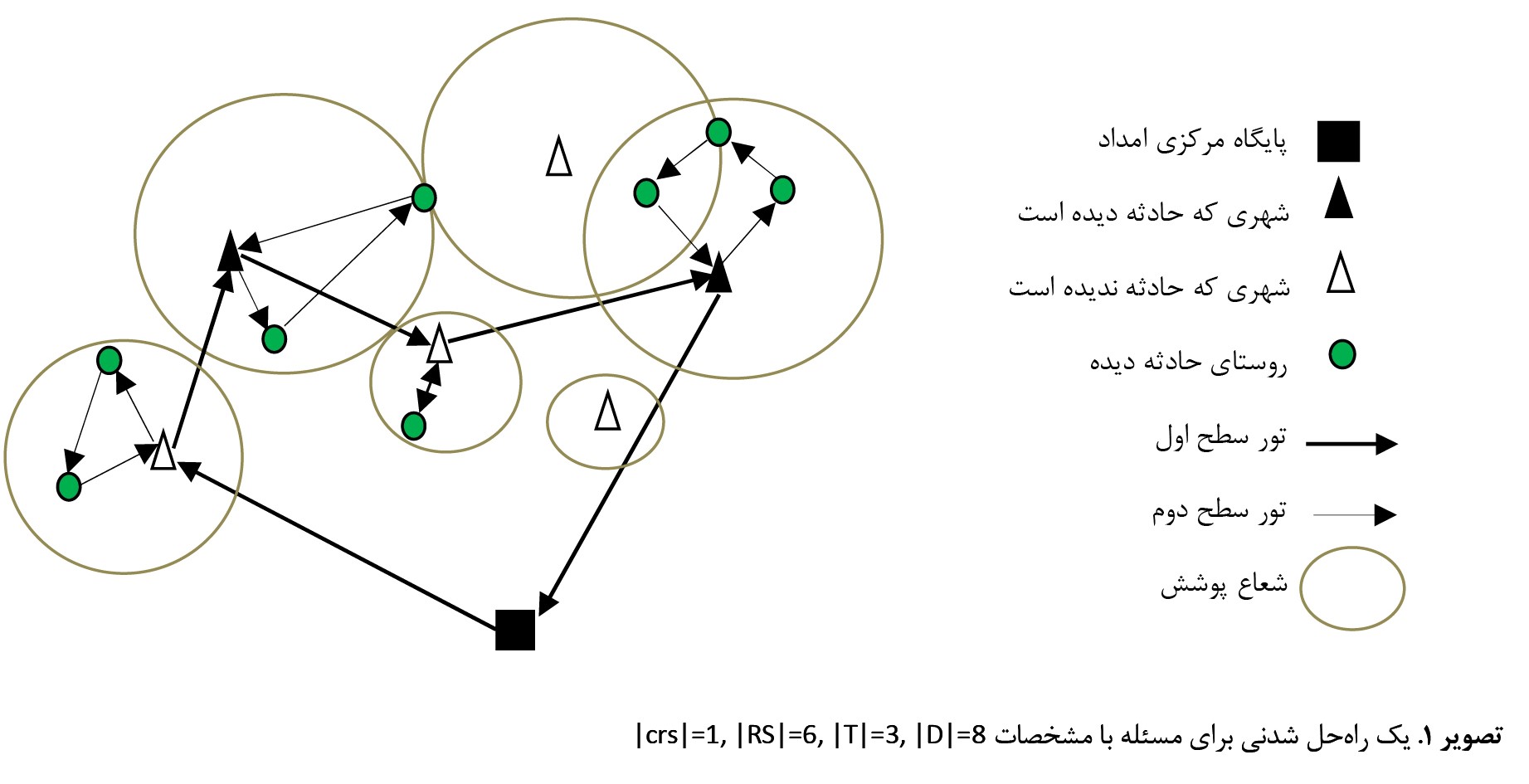
این مثال شامل 15 رأس است که از این 15 رأس، یک پایگاه امداد مرکزی (crs)، 6 شهر (RS) که از این شهرها، 2 شهر باید در تور قرار گیرند و 4 شهر دیگر می‌توانند در تور واقع شوند. همچنین 8 نقطه حادثه‌دیده وجود دارد (D). همه نقاط حادثه‌دیده از‌طریق پایگاه‌های امداد برپا‌شده در شهرهای قرار‌گرفته در تور امداد‌رسانی شده‌اند. همچنین در این شکل نحوه امداد‌رسانی از پایگاه اصلی به پایگاه‌های برپا‌شده در تور سطح اول و سپس امداد‌رسانی از این پایگاه‌ها به نقاط حادثه‌دیده در سطح دوم به ترتیب و به‌طور هم‌زمان نمایش داده شده‌اند. 
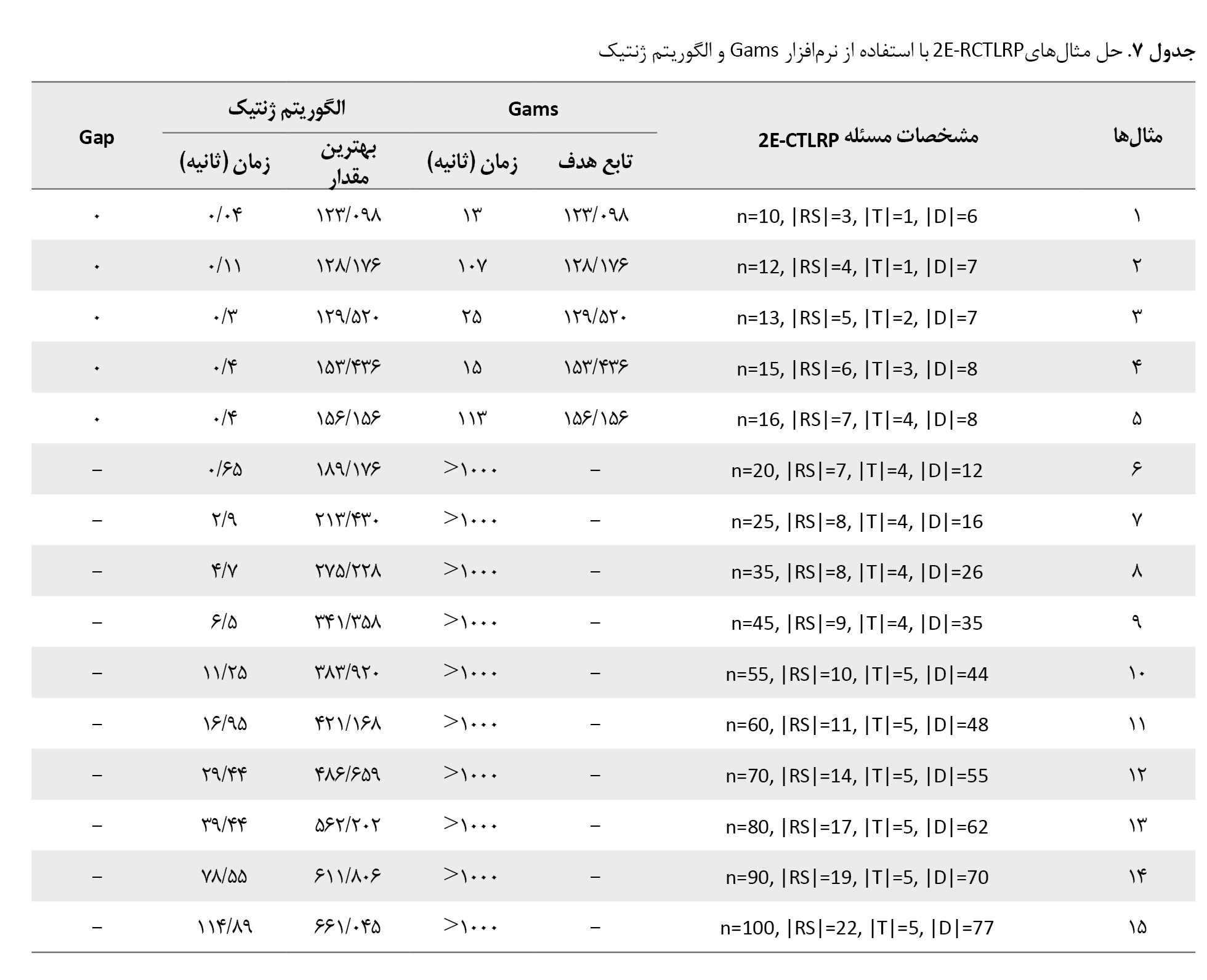
مسئله تور پوششی دو سطحی در شرایط امداد‌رسانی بر روی گراف کامل G=(V,E) که در آن V برابر با R S U D U {crs} مجموعه رئوس و E مجموعه یال‌هاست، تعریف می‌شود. RS مجموعه پایگاه‌های امداد‌رسان شهری است که به 2 دسته تقسیم می‌شود: دسته اول شامل آن دسته از پایگاه‌ها است که لزوماً باید برپا شوند و دسته دوم شامل پایگاه‌هایی است که می‌توانند جهت امدادرسانی به نقاط حادثه‌دیده، برپا شوند. رأس crs که بیانگر پایگاه مرکزی امدادرسانی است، باید در تور قرار گیرد و بنابراین به مجموعه T تعلق دارد . مجموعه T شامل برخی از رئوس مجموعه RS و پایگاه مرکزی است. بنابراین داریم . مجموعه D شامل نقاط حادثه‌دید‌ه‌ای است که باید توسط پایگاه‌های امداد برپاشده امداد‌رسانی شوند.
توجه شود که هر نقطه حادثه‌دیده فقط می‌تواند توسط پایگاه‌هایی امداد‌رسانی شود که در فاصله پوششی آن قرار داشته باشند. این فاصله پوششی برای رئوس مجموعه RS باتوجه‌به میزان امکانات موجود در آن‌ها متفاوت است. در این مسئله مجموعه‌ای از متقاضیان دریافت امداد (نقاط حادثه‌دیده)، مجموعه‌ای از نقاط (شهرهای حادثه‌دیده) که باید در آن‌ها پایگاه امداد برپا شود و مجموعه‌ای از نقاط (شهرهای آسیب‌ندیده) که می‌توان در آن‌ها پایگاه‌های امداد‌رسانی برپا کرد، وجود دارد. مقدار تقاضای نقاط آسیب‌دیده و ظرفیت پایگاه‌ها از ابتدا مشخص هستند. وسایل حمل‌و‌نقل کالا در هر سطح، مشابه و دارای ظرفیتی یکسان هستند. همچنین این مسئله شامل 2 مجموعه از مسیرهای وسایل حمل‌و‌نقل نیز هست. مسیرهای سطح اول بر روی مجموعه RS تعریف می‌شوند به این صورت که در شهرهای مجموعه T حتماً باید پایگاه‌های امداد برپا شوند و در بقیه شهرها می‌توان پایگاه‌های امداد جهت خدمت‌رسانی به نقاط حادثه‌دیده برپا کرد (فرمول شماره 1).


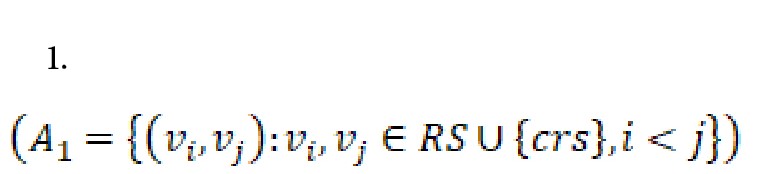
 امداد‌رسانی در سطح دوم باتوجه‌به امکانات آن سطح، صرفاً به نقاط آسیب‌دیده‌ای امکان‌پذیر است که در فاصله کمتری از یک شعاع معین نسبت به پایگاه امداد متناظر قرار داشته باشند (فرمول شماره 2).


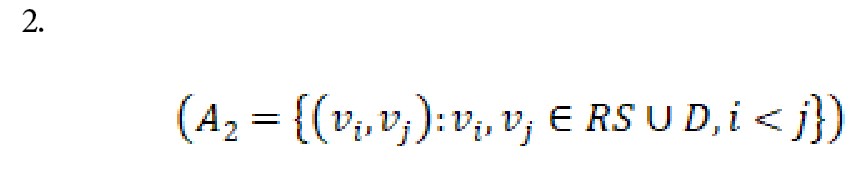
هدف از این مسئله، کمینه کردن هزینه‌های مربوطه، تعیین مکان‌های مناسب احداث پایگاه‌های امداد، تعیین و برنامه‌ریزی تورهای وسایل نقلیه در هر سطح است. به‌طوری‌که همه تقاضاها برآورده شوند. در این مقاله فرض شده است که پایگاه مرکزی امداد و پایگاه‌های امداد برپا‌شده می‌توانند کل مقدار تقاضا را برآورده کنند. یک راه‌حل شدنی شامل زیرمجموعه‌ای از پایگاه‌های امداد برپا‌شده و یک زیرمجموعه از مسیرهای سطح اول و دوم است. در ضمن محدودیت‌های زیر باید اعمال شوند:
هر نقطه حادثه‌دیده باید توسط تنها یک وسیله نقلیه سطح دوم خدمت‌رسانی شود و هر مرکز پایگاه امداد برپا‌شده باید تنها توسط یک وسیله نقلیه سطح اول تأمین شود. کل مقدار کالای تحویل‌شده توسط یک وسیله نقلیه نمی‌تواند از ظرفیت آن وسیله تجاوز کند. هر مسیر سطح دوم باید از یک پایگاه امداد برپا‌شده شروع شده و در همان پایگاه پایان یابد. کل مقدار کالای دریافت‌شده توسط یک پایگاه امداد باید به‌طور کامل به متقاضیان تحویل داده شود (ذخیره‌سازی مجاز نیست). تابع هدف که کل هزینه سیستم است و شامل هزینه استقرار پایگاه‌های امداد، هزینه‌های ثابت وسایل نقلیه استفاده‌شده و هزینه‌های مسیرهای سطح اول و سطح دوم، باید حداقل شود. برای بیان مدل‌سازی ریاضی برنامه‌ریزی عدد صحیح مختلط مسئله مورد‌تحقیق، ابتدا نمادها و پارامترهای به‌کار‌رفته در مدل ریاضی تشریح می‌شوند.سپس با افزودن ملاحظات مربوط به محدودیت‌های پوشش به مسئله مسیریابی ـ مکان‌یابی 2 سطحی ارائه‌شده توسط نگوین و همکاران (2012 ب) مسئله مورد‌تحقیق مدل‌سازی می‌شود. 

 مجموعه‌های مسئله
 V مجموعه کل رئوس برابر با R S U D U {crs}
RS مجموعه کل شهرها
D مجموعه روستاهای حادثه‌دیده
T مجموعه شهرهای حادثه‌دیده
A1 مجموعه مسیرهای سطح اول
A2 مجموعه مسیرهای سطح دوم
K مجموعه وسایل نقلیه سطح اول
 L مجموعه وسایل نقلیه سطح دوم


 
 فرمول شماره 3 حاوی رئوسی از مجموعه  است که می‌توانند برای پوشش رأس  در فاصله پوششی  استفاده شوند. 

پارامترهای مسئله
Os هزینه برپا شدن پایگاه امداد s
As ظرفیت پایگاه امداد s
Dj مقدار تقاضای امدادی روستای j
Q ظرفیت وسایل نقلیه سطح اول
R ظرفیت وسایل نقلیه سطح دوم
F هزینه ثابت استفاده از وسایل نقلیه سطح اول
G هزینه ثابت استفاده از وسایل نقلیه سطح دوم
Rs شعاع پوششی پایگاه امداد s
dis_sd فاصله نقطه  sERSو dED
Cij هزینه طی مسافت از گره i به گره j

متغیرهای مسئله

X^k_ij اگر وسیله نقلیه سطح اول  k کمان (i,j) را پیموده باشد 1 و در غیر این صورت صفر است. 

Y^l_ij اگر وسیله نقلیه سطح دوم l کمان (i,j) را پیموده باشد 1 و در غیر این صورت صفر است. 
Zs اگر پایگاه امداد sERS برپا شده باشد 1 و در غیر این صورت صفر است.
Usd اگر پایگاه امداد sERS به نقطه حادثه‌دیده dED خدمت‌رسانی کرده باشد 1 و در غیر این صورت صفر است.
متغیر نامنفی b^k_s مقدار کالای تحویل داده‌شده به پایگاه امداد sERS توسط وسیله نقلیه kEK را نشان می‌دهد. 
باتوجه‌به موارد ذکر‌شده، مدل برنامه‌ریزی عدد صحیح مختلط مسئله تور پوششی دو سطحی در شرایط امداد‌رسانی به‌صورت فرمول‌های شماره 4، 5، 6، 7، 8، 9، 10، 11، 12، 13، 14، 15، 16، 17، 18، 19، 20، 21، 22، 23، 24، 25، 26 ، 27 ارائه می‌شود:





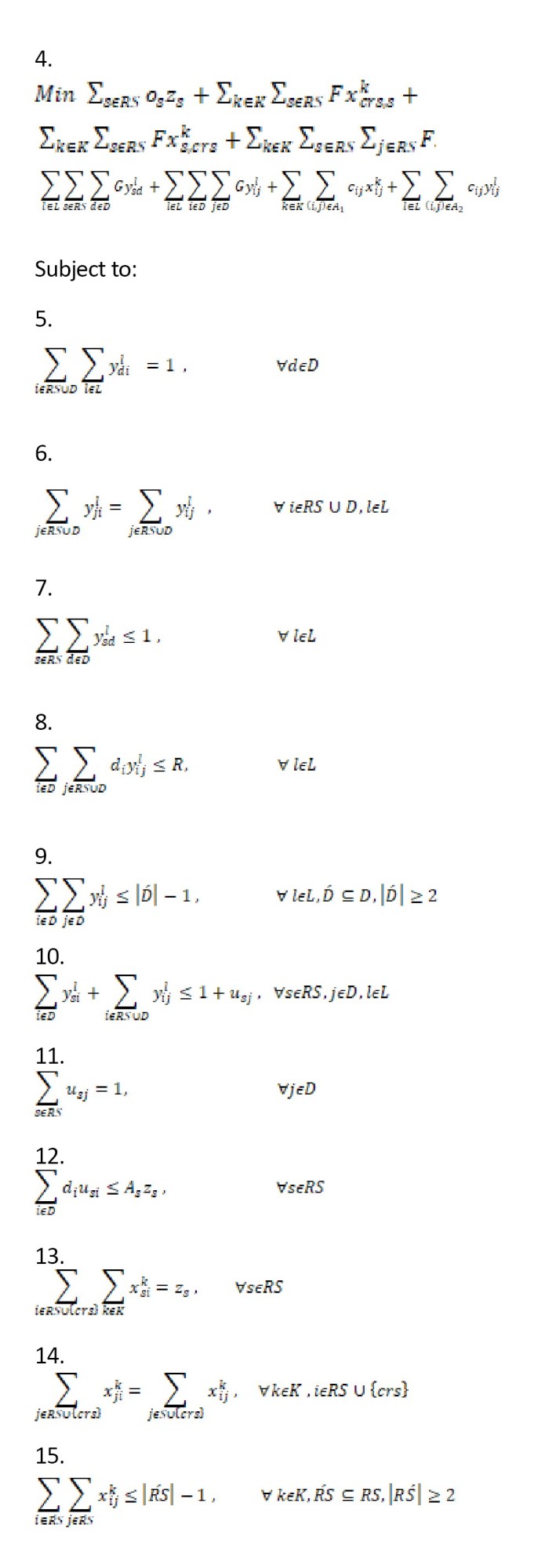
تابع هدف 1 شامل هزینه‌های برپایی پایگاه‌های امداد، هزینه‌های ثابت استفاده از وسایل نقلیه سطح اول و دوم و هزینه‌های مسیریابی هر دو سطح است. محدودیت‌های 2 تا 9 مربوط به سطح دوم است. محدودیت 2 تضمین می‌کند که تمام نقاط حادثه‌دیده بازدید شوند. محدودیت 3 تضمین می‌کند یک وسیله نقلیه سطح دوم به پایگاه امداد اولیه‌اش برگردد. در محدودیت 4، هر وسیله نقلیه سطح دومی حداکثر از یک پایگاه امداد حرکت می‌کند. محدودیت 5 مربوط به ظرفیت وسایل نقلیه سطح دوم است. محدودیت 6 مربوط به حذف زیرتورها است. محدودیت 7 تضمین می‌کند پایگاه امداد s به نقطه حادثه‌دیده j خدمت‌رسانی می‌کند (Usj=1). اگر یک وسیله نقلیه lEL وجود داشته باشد که پایگاه امداد s را ترک کرده و به نقطه حادثه‌دیده Usj رسیده باشد. همچنین  می‌تواند مساوی 1 باشد حتی اگر هیچ وسیله نقلیه‌ای از s به j نرفته باشد. محدودیت 8 دبرای تخصیص هر نقطه حادثه‌دیده به 1 پایگاه امداد به کار می‌رود. محدودیت 9 بیان می‌دارد اگر پایگاه امداد s برپا نشده باشد آن‌گاه هیچ نقطه حادثه‌دیده‌ای به آن تخصیص نمی‌یابد و در غیر این صورت اگر پایگاه امداد ss برپا شده باشد، آن‌گاه کل تقاضای تخصیص یافته به آن نمی‌تواند از ظرفیتش تجاوز کند. 
محدودیت‌های 10 تا 17 مربوط به سطح اول هستند. محدودیت 10 بیان می‌دارد که هر پایگاه امداد برپا‌شده باید توسط 1 وسیله نقلیه سطح اول بازدید شود. محدودیت 11 یک سفر پیوسته را برای هر وسیله نقلیه به کار گرفته‌شده در سطح اول تضمین می‌کند. محدودیت 12 مربوط به حذف زیر‌تورها است. محدودیت 13 مقدار جریان را در هر پایگاه امداد s نشان می‌دهد به این صورت که کل مقدار کالای آورده‌شده به پایگاه امداد s توسط وسایل نقلیه k سطح اول باید با کل تقاضای تخصیص‌یافته به این پایگاه امداد s برابر باشد (ذخیره‌سازی مجاز نیست). محدودیت 14 مربوط به ظرفیت وسایل نقلیه سطح اول است. محدودیت 15 بیان می‌دارد اگر وسیله نقلیه k پایگاه امداد s را بازدید نکرده باشد، مقدار کالای ارائه‌شده توسط وسیله نقلیه k به پایگاه امداد s باید صفر باشد. محدودیت‌ 16 تضمین می‌کند هر نقطه حادثه‌دیده فقط به 1 پایگاه‌های امدادی که در فاصله پوششی آن قرار دارد تخصیص یابد. محدودیت 17 تضمین می‌کند در نقاط مجموعه T حتماً باید پایگاه امداد برپا شود. محدودیت‌های 18 تا 23 متغیرهای تصمیم مسئله را تعریف می‌کنند. 

روش حل مسئله
برای حل این مسئله از روش‌های دقیق و فراابتکاری در این مقاله استفاده شده است. این مسئله یک مسئله Np-hard می‌باشد، زیرا تعمیمی از مسائل شناخته‌شده Np-hard مانند مسئله مسیریابی ـ مکان‌یابی 2 سطحی (2E-LRP) تعریف شده در مقاله (نگوین، پرینس و پرودون، 2012ب) و مسئله تور پوششی بیان‌شده در مقاله (ژاندرُ و همکاران، 1997) است. در ابتدا مسئله در ابعاد کوچک توسط نرم‌افزار بهینه‌سازی Gams به‌صورت دقیق حل می‌شود. ازآنجایی‌که این مسئله در حوزه مسائل Np-hard قرار دارد و با بزرگ‌تر شدن ابعاد مسئله، روش‌های دقیق قادر به حل آن‌ها در یک زمان منطقی و قابل‌قبول نیستند، برای ابعاد بزرگ‌تر مسئله از روش فراابتکاری الگوریتم ژنتیک استفاده می‌شود. به این صورت مسئله مذکور در نرم‌افزار متلب کدنویسی شده و سپس حل شده است. با مقایسه جواب‌ها بعد از حل مسئله در ابعاد کوچک، با استفاده از هر دو روش دقیق و فراابتکاری مشاهده می‌شود جواب‌ها کاملاً یکسان هستند. بنابراین عملکرد الگوریتم ژنتیک مورد تأیید و قابل‌استفاده برای مثال‌های در ابعاد بزرگ است. 

الگوریتم ژنتیک پیشنهادی برای حل مسئله 
نمایش جواب و تولید جواب شدنی
برای مسئله مورد بررسی در این تحقیق یک جواب شدنی، شامل مکان‌یابی پایگاه‌های امداد‌رسانی و مسیریابی وسایل حمل‌و‌نقل در دو سطح است. در سطح اول مسئله، پایگاه‌های امداد برپا‌شده در شهرها توسط پایگاه مرکزی امداد و به‌وسیله وسایل نقلیه مستقر در این پایگاه تأمین می‌شوند. در سطح دوم، روستاهای بحران‌زده تخصیص‌یافته به هر پایگاه امداد، توسط وسایل نقلیه مستقر در آن پایگاه‌ها امداد‌رسانی می‌شوند. برای توضیح بیشتر، روند الگوریتم ژنتیک برای مثال 4 جدول شماره 7 تشریح می‌شود. این مثال شامل 15 رأس است که از این 15 رأس، 1رأس مربوط به پایگاه امداد مرکزی، 6 رأس نشان‌دهنده شهرها  و 8 رأس مربوط به نقاط حادثه‌دیده (روستاها) هستند . از مجموع 6 شهر، شهرهای 2 و 6 باید در تور قرار گیرند و 4 شهر دیگر می‌توانند جهت امداد‌رسانی به روستاها در تور قرار گیرند. بنابراین باتوجه‌به اینکه پایگاه مرکزی امداد نیز در تور سطح اول قرار می‌گیرد، 3 رأس باید در تور قرار گیرد . ماتریس Subtours را در نظر بگیرید؛ تعداد سطرهای این ماتریس برابر با تعداد شهرها و تعداد ستون‌های این ماتریس برابر با حداکثر تعداد روستاهای تخصیص داده‌شده به یک شهر است. بنابراین ماتریس Subtours به این ‌صورت ساخته می‌شود: در ابتدا عنصر اول هر سطر از ماتریس برابر با شماره 1 شهر قرار می‌گیرد و سپس روستاها باتوجه‌به شعاع پوشش شهرها به آن‌ها تخصیص می‌یابند:


سپس در انتهای هر سطر از ماتریس Subtours شهری که در ابتدای آن سطر قرار گرفته بود، قرار داده می‌شود. به عنوان مثال، ماتریس Subtours می‌تواند به‌صورت جدول شماره 2 باشد. 


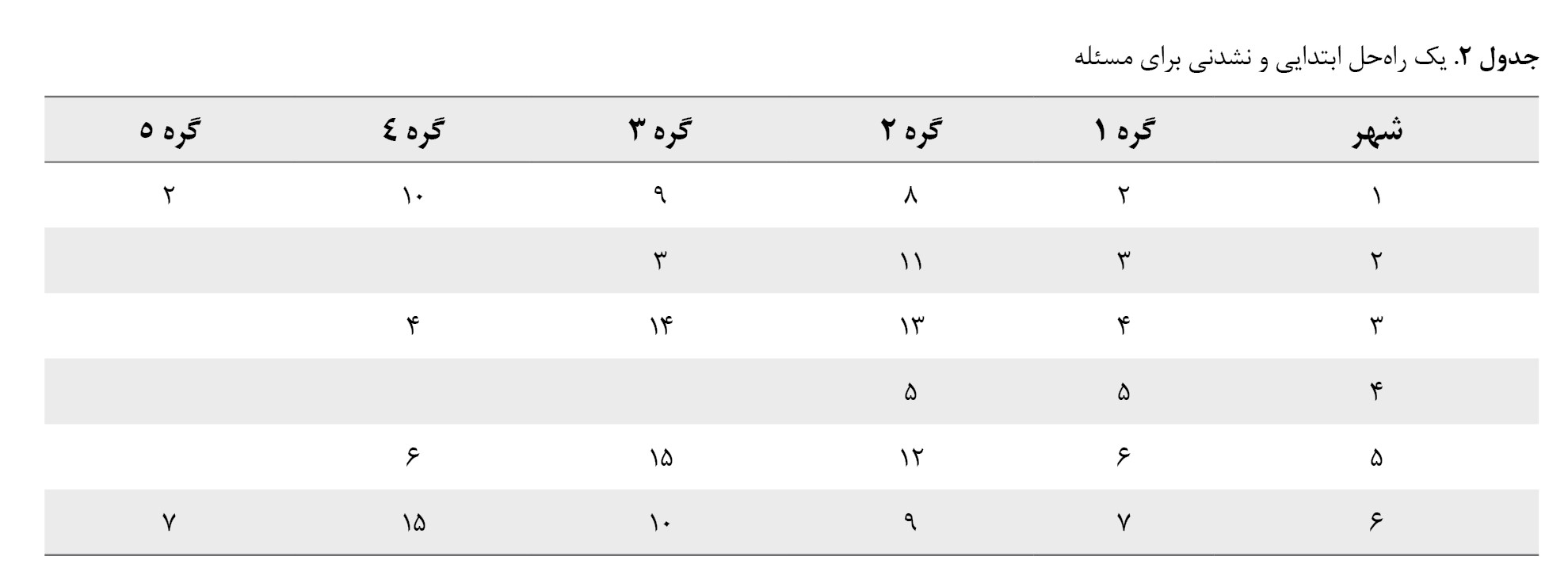
در‌واقع ماتریس Subtours شامل زیر‌تورهای مسئله است که از هر پایگاه امداد شروع شده و در همان پایگاه خاتمه می‌یابند. ماتریس Subtours باید دارای 2 ویژگی باشد: اولاً تمامی روستاها در این ماتریس وجود داشته باشند و ثانیاً هر روستا فقط 1 بار ظاهر شده باشد. شرط اول بیان می‌کند که تمامی روستاها توسط شهرها پوشش یافته‌اند و شرط دوم بیانگر آن است که هر روستا فقط به یک شهر تخصیص یافته باشد. در ماتریس مذکور شرط اول برقرار است، اما در‌مورد شرط دوم باید گفت روستاهای 9 و 10 و 15 به 2 شهر تخصیص یافته‌اند، بنابراین برای شدنی بودن مسئله، به‌طور تصادفی در ماتریس مذکور روستاهای تکراری حذف می‌شوند تا زمانی که شرط دوم برقرار شود و هر روستا فقط به 1 شهر تخصیص داده شده باشد. بنابراین ماتریس Subtours می‌تواند به‌صورت جدول شماره 3 باشد. 


در ادامه شهرهایی که جزو مجموعه T نیستند و روستایی نیز به آن‌ها تخصیص نیافته است حذف می‌شوند. به این ترتیب شهر 5 نیز در تور قرار نمی‌گیرد و از ماتریس Subtours حذف می‌‌شود.در ادامه تور مورد‌نظر با قرار دادن سطرهای ماتریس Subtours پشت سر هم و افزودن پایگاه امداد مرکزی (عدد شماره 1) در ابتدا و انتهای آن ساخته می‌شود. بنابراین یک راه‌حل شدنی اولیه برای این مثال به‌صورت زیراست:
Tour=1-2-8-2-3-11-3-4-13-14-4-6-12-15-6-7-9-10-7-1

عملگر تقاطع
از این عملگر برای جست‌وجوی محلی در فضای پاسخ استفاده می‌شود و دارای انواع مختلفی، مانند 1 نقطه‌ای، 2 نقطه‌ای، چندنقطه‌ای و غیره است. در این مقاله به‌منظور تولید 2 مسیر جدید از 2 مسیر اولیه از عملگر 1 نقطه‌ای استفاده شده است. فرض کنید 2 والد به‌صورت جداول شماره 4 و 5 داشته باشیم. 





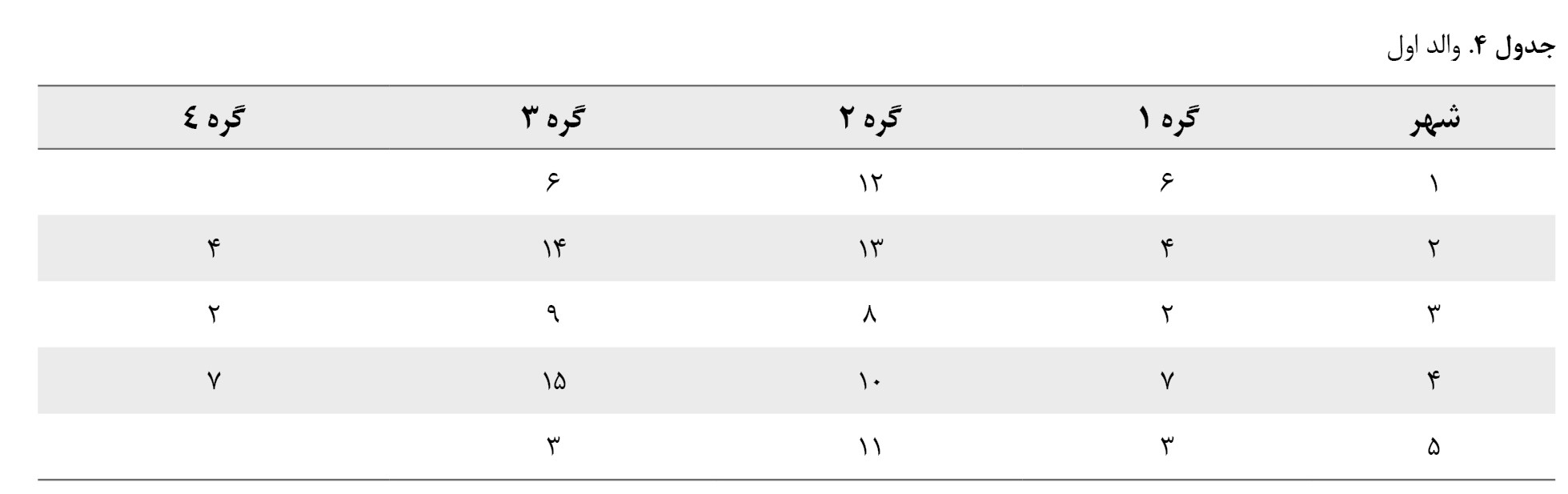
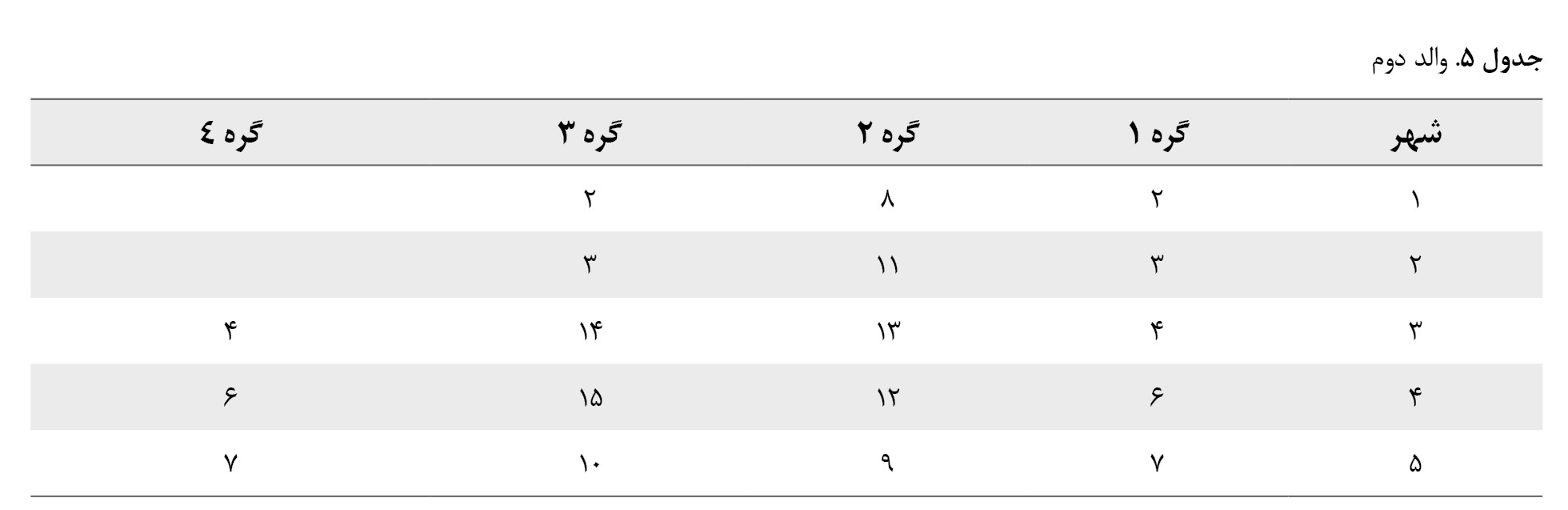
والد اول با Oldtour 1 و والد دوم با Oldtour 2 نام‌گذاری می‌شوند، بنابراین داریم:
Oldtour1= 1-6-12-6-4-13-14-4-2-8-9-2-7-10-15-7-3-11-3-1
Oldtour2=1-2-8-2-3-11-3-4-13-14-4-6-12-15-6-7- 9-10-7-1
حال عددی از بین پایگاه‌های امداد مستقر در شهرها که در هر دو تور وجود داشته باشد به تصادف انتخاب می‌شود.این عدد همان نقطه تقاطع Crosspoint است. فرض کنید Crosspoint=2 انتخاب شده باشد. برای به‌وجود آوردن تورهای جدید (فرزندها) با استفاده از تورهای قدیم (والدها)، جای زیر‌تورهایی که با شهر شماره 2 شروع می‌شود، در تورهای قدیم با هم عوض می‌شوند و تورهای جدید باتوجه‌به فاصله پوششی شهرها و اینکه همه روستاها باید در تور وجود داشته باشند و هر روستا نیز فقط 1 بار در تور وجود داشته باشد، به وجود می‌آیند. بنابراین باتوجه‌به جابه‌جایی زیرتورها در تورهای جدید، در تور جدید اول، به علت تکراری بودن روستای 9، این روستا حذف شده و در تور جدید دوم، باتوجه‌به فاصله پوششی شهر 7 و اینکه روستای 9 می‌تواند به این شهر تخصیص یابد، این روستا اضافه شده است. فرزند اول با Newtour1 و فرزند دوم با Newtour 2 نام‌گذاری می‌شوند:
Newtour1=1-6-12-6-4-13-4-2-8-2-7-9-10-15-7-3- 11-3-1
Newtour2=1-2-8-9-2-3-11-3-4-13-4-4-6-12-15-6- 7-10-7-1
حال تورهای فرزند به‌وجود‌آمده قطعاً شدنی نیز هستند. برای تسریع در رسیدن به بهترین تور، می‌توان از عملگر 2 نقطه‌ای یا چند‌نقطه‌ای نیز استفاده کرد. به این صورت که به‌جای انتخاب 1 شهر، 2 یا چند شهر به‌طور تصادفی انتخاب شوند و جای زیرتورهای مرتبط با آن‌ها در تورهای والد عوض شود.

عملگر جهش
بعد از اجرای عملگر تقاطع بر روی تورهای قدیم و به وجود آوردن تورهای جدید، استفاده از عملگر جهش بر روی تورهای جدید و به دست آوردن تورهای جهش‌یافته جهت رسیدن به بهترین تورها، لازم به نظر می‌آید. برای این کار، یک یا چند پایگاه امداد مستقر در تور جدید به تصادف انتخاب می‌شود و سپس ترتیب قرار گرفتن روستاها در آن زیر‌تور به‌طور تصادفی تغییر می‌یابد. به‌عنوان مثال فرض کنید برای Newtour1 عدددهای تصادفی تولید‌شده 2 و 4 باشند، تور جهش یافته (Mutatedtour) می‌تواند به‌صورت زیر باشد:
Newtour 1=1-2-8-9-2-3-11-3-4-13-14-4-6-12-15-6-7-10-7-1
Mutatedtour= 1-2-9-8-2-3-11-3-4--14-13-4-6-12-15-6-7-10-7-1

عملگر انتخاب
برای تولید نسل جدید از عملگر انتخاب استفاده می‌شود. نسل جدید در این مسئله شامل تعدادی از تورهای برتر نسل قبل، تورهای جدید تولید‌شده و تورهای جهش‌یافته است. این عمل با استفاده از عملگر چرخ رولت صورت می‌پذیرد. درصد مربوط به هر قسمت باتوجه‌به طراحی آزمایش‌ها برای هر مثال به دست آمده است. مثلاً برای مثال 4، 60 درصد جمعیت نسل جدید از عملگر تقاطع، 20 درصد از عملگر جهش و 20 درصد بقیه نیز از جمعیت برتر نسل قبل به‌وجود آمده‌اند.
شبه کد الگوریتم ژنتیک استفاده‌شده در این مقاله به‌صورت زیر است:
-پارامترهای اولیه الگوریتم را تعیین کنید.
-جمعیت اولیه از تورها را به‌صورت تصادفی تولید کنید.
-مقدار تابع هدف برای هر یک از تورها را محاسبه کنید.
-برای i=1  تا تعداد نسل‌ها تکرار کنید.
- برنامه تورها (بعنوان والدین) را انتخاب کنید.
-تورهای جدید را براساس عملگرهای ادغام و جهش تولید کنید.
-مقدار تابع هدف برای تورهای جدید را محاسبه کنید.
-اعضای نسل جدید را از داخل اعضای نسل قبل و تورهای جدید ایجادشده انتخاب کنید.

استفاده از طراحی آزمایش‌ها برای تنظیم پارامترهای الگوریتم ژنتیک
پارامترهای الگوریتم ژنتیک پیشنهادی برای مسئله تور پوششی 2 سطحی تعریف‌شده در این مقاله نرخ جهش، نرخ تقاطع، جمعیت و تعداد تکرارها هستند. برای تعیین اثر تغییر این پارامترها روی کیفیت جواب‌ها از طرح آزمایشی تاگوچی استفاده شده است. برای هریک از عوامل 3 سطح در نظر گرفته شده است. نرخ تقاطع 0/6، 0/7، 0/8، نرخ جهش 0/1، 0/15،0/2، جمعیت 40، 50، 60 و برای حداکثر تکرارها 400، 600، 800 در نظر گرفته شده است. برای حل هر‌یک از مسائل، تنظیم پارامترها انجام گرفته و در‌نهایت مسئله با الگوریتم تنظیم‌شده حل شده است. به‌عنوان نمونه در جدول شماره 6 برای مثال10 از جدول شماره 7، طرح آزمایش تاگوچی دارای 9 آزمایش بوده که توسط نرم‌افزار مینی‌تب به دست آمده است.


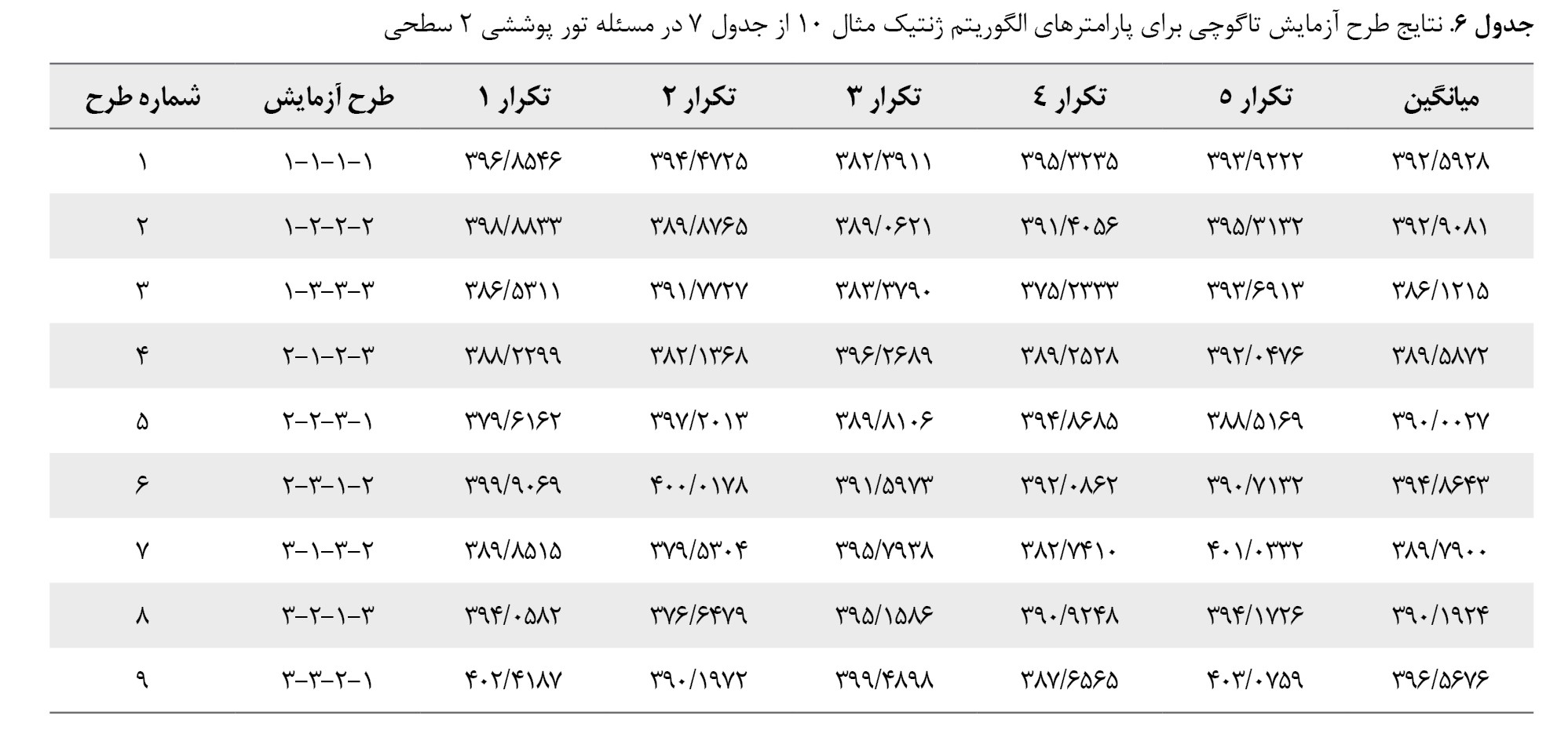
در ستون آخر، جواب الگوریتم ژنتیک به‌صورت میانگین بعد از 5 بار تکرار آورده شده است. 
 با در نظر گرفتن ستون میانگین در نرم‌افزار مینی تب و باتوجه‌به تصویر شماره 2، طرح 1-2-3-3 به‌عنوان بهترین طرح معرفی می‌‌شود. یعنی برای مثال 10 نرخ تقاطع 0/8، نرخ جهش 0/2، تعداد جمعیت 50 و حداکثر تعداد تکرارها برابر 400 در نظر گرفته شده است.

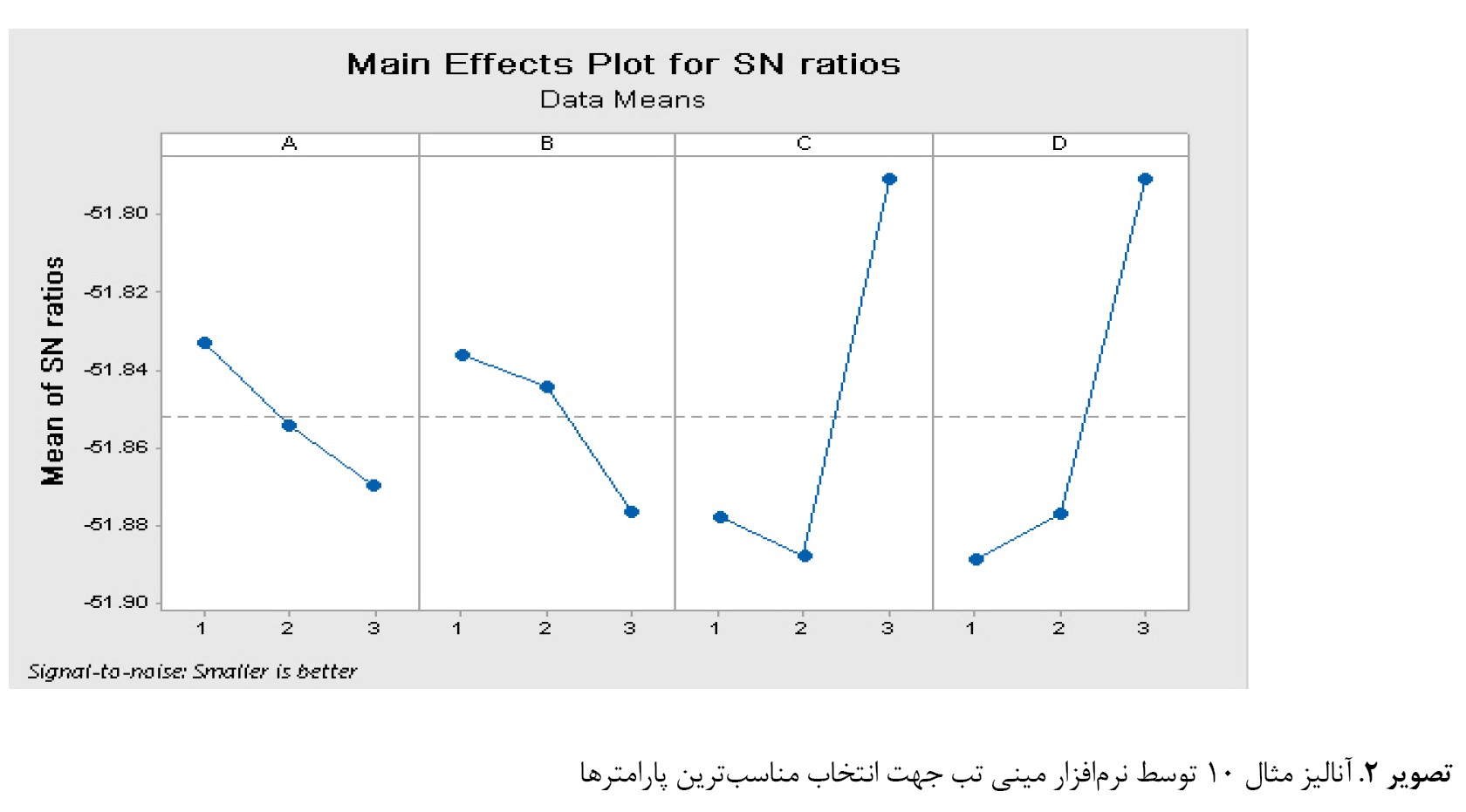
با وارد کردن اعداد بالا در الگوریتم ژنتیک مذکور و بعد از 10 بار اجرا توسط نرم‌افزار متلب، جواب به‌صورت میانگین برابر 383/920 شده است. برای تمامی مثال‌ها آزمایش تاگوچی انجام گرفته و مثال‌ها با پارامترهای تنظیم‌شده حل شده‌اند. 

مثال‌های عددی
در این بخش 15 مثال در اندازه‌های مختلف برای مسئله تور پوششی 2 سطحی در شرایط امداد‌رسانی بررسی و حل شده است. در این مثال‌ها تعداد رئوس از 10 تا 100 رأس در نظر گرفته شده است. مجموعه  بیانگر مجموعه شهرها، مجموعه  شامل پایگاه مرکزی به علاوه شهرهایی که باید در تور قرار گیرند و مجموعه  شامل روستاهای حادثه‌دیده است که باید امداد‌رسانی شوند. در ابتدا برای 5 مثال اول کدنویسی در نرم‌افزار Gams انجام گرفته و جواب‌ها به‌صورت دقیق به همراه زمان حل آن‌ها آورده شده‌اند. در ادامه با استفاده از الگوریتم ژنتیک برای 5 مثال ابتدایی، کدنویسی در نرم‌افزار متلب انجام گرفته، مثال‌ها حل شده و جوا‌بها به همراه زمان حل آن‌ها آورده شده‌اند. با مقایسه جواب‌های به‌دست‌آمده مشاهده می‌شود نتایج حل مسائل با استفاده از الگوریتم ژنتیک و نرم‌افزار Gams کاملاً یکسان است و کد نوشته‌شده برای مسئله با استفاده از الگوریتم ژنتیک کارایی لازم را برای حل مثال‌های با ابعاد بزرگ‌تر دارد. از‌آنجایی‌که با افزایش ابعاد مسئله، زمان حل آن‌ها در نرم‌افزار Gams به‌شدت افزایش می‌یابد در ادامه برای حل این مسائل از الگوریتم ژنتیک و کدنویسی در نرم‌افزار متلب استفاده شده است. انجام تمامی محاسبات در کامپیوتری با مشخصات CPU: Intel Core i5-4200U, 1.6GHz و RAM: 4GB انجام گرفته است. نتایج در جدول شماره 7 قابل‌مشاهده هستند.
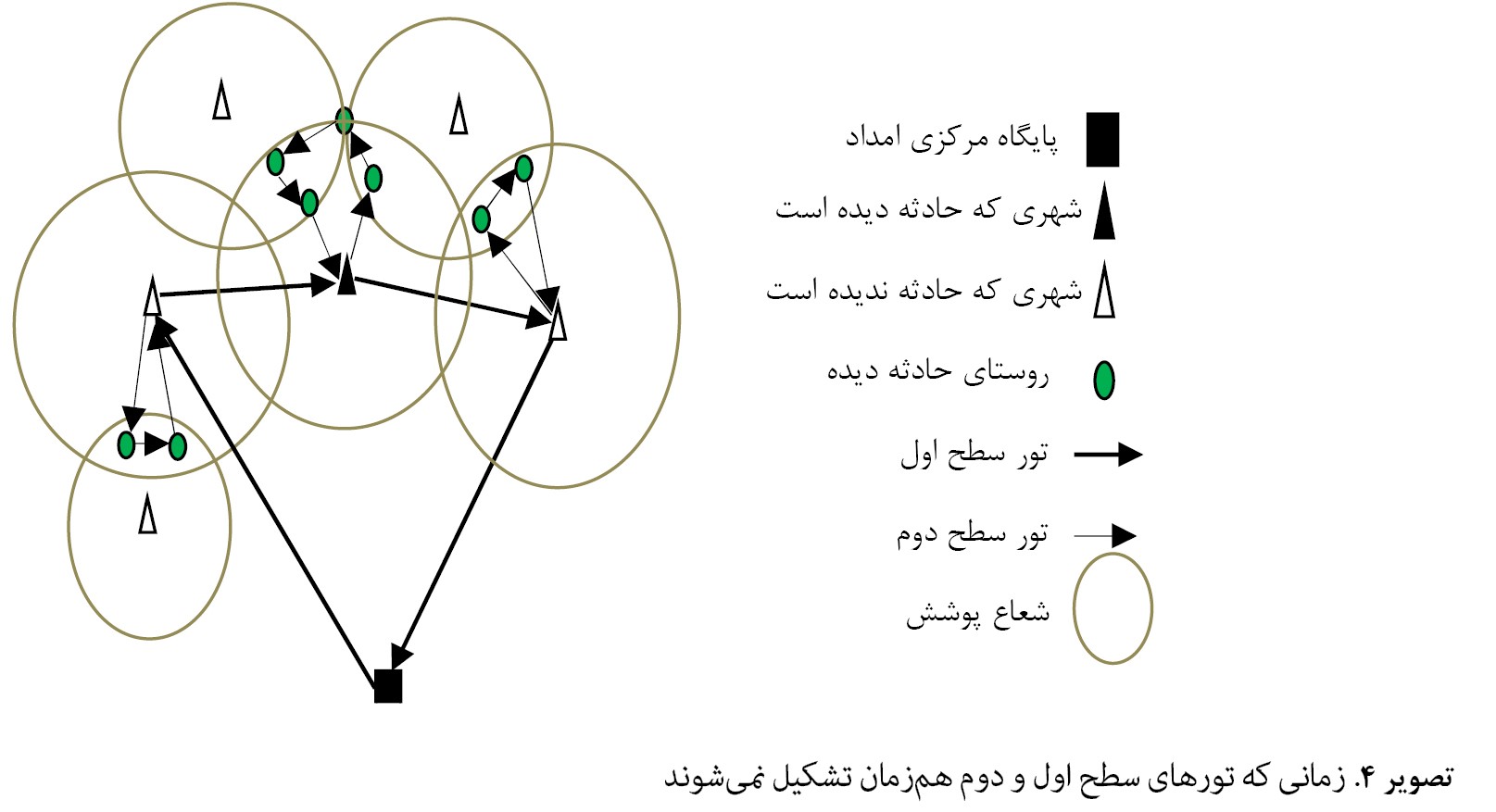
در اینجا برای درک بهتر مثال‌ها به تشریح مثال 4 از جدول شماره 7 پرداخته می‌شود. این مثال شامل 15 رأس است که از این 15 رأس، یک رأس مربوط به پایگاه امداد مرکزی، 6 رأس نشان‌دهنده شهرها  با شعاع‌های پوشش متفاوت و 8 رأس مربوط به نقاط حادثه‌دیده (روستاها) هستند . از مجموع 6 شهر، 2 شهر باید در تور قرار گیرند و 4 شهر دیگر می‌توانند جهت امداد‌رسانی به روستاها در تور قرار گیرند. بنابراین باتوجه‌به اینکه پایگاه مرکزی امداد نیز در تور سطح اول قرار می‌گیرد بنابراین 3 رأس باید در تور قرار گیرند . بعد از حل مثال مشخص شد برای امداد‌رسانی به همه روستاهای حادثه‌دیده لازم است 4 شهر در تور سطح اول قرار گیرند و در آن شهرها پایگاه‌های امدادرسانی برپا شود. سپس امداد‌رسانی از 4 پایگاه امداد برپا‌شده به روستاهای حادثه‌دیده توسط تورهای سطح دوم انجام گیرد. مقدار هزینه امداد‌رسانی در این مثال در حالت بهینه برابر با 153/436 واحد شده است. توجه شود که مثال‌های ارائه‌شده برای این مسئله با در نظر گرفتن این اصل که دو سطح به‌صورت هم‌زمان تشکیل می‌شوند، حل شده‌اند. شاید این‌گونه به نظر برسد که در ابتدا می‌توان مسئله را به‌صورت یک مسئله تور پوششی ساده حل کرد و سپس بعد از به دست آوردن تور سطح اول و تخصیص نقاط حادثه‌دیده به پایگاه‌های امداد مستقر در تور سطح اول، تورهای سطح دوم را که هر‌کدام یک مسئله TSP ساده هستند تشکیل داد. در این قسمت با ارائه مثالی نشان داده می‌شود این دیدگاه صحیح نیست و با حل هم‌زمان و غیرهم‌زمان، جواب‌های مختلفی به دست می‌آید. این مثال از 15 رأس تشکیل شده است که 6 رأس آن شهرها و 8 رأس دیگر نقاط حادثه‌دیده و یک رأس مربوط به پایگاه مرکزی امداد هستند. کل مسافت پیموده‌شده در حالت هم‌زمانی تورها برابر با 71/4582 واحد و در حالت غیرهم‌زمان برابر با 73/6704 واحد است. جواب مثال در هر دو حالت در قالب تصاویر شماره 3 و 4 آورده شده است.

تحلیل حساسیت مسئله
در این قسمت تحلیل حساسیت مسئله از چند جنبه بررسی می‌شود. هدف از انجام تحلیل حساسیت در این پژوهش، بررسی میزان تأثیر تغییر در پارامترهای کلیدی مدل بر نتایج نهایی و ساختار تصمیم‌گیری است. در شرایط بحرانی، تصمیم‌گیرندگان ممکن است با عدم‌قطعیت در برخی پارامترها، مانند ظرفیت وسایل حمل‌ونقل یا شعاع پوشش پایگاه‌ها مواجه باشند. در این پژوهش، 2 پارامتر حیاتی تحت تحلیل حساسیت قرار گرفتند: تحلیل حساسیت نسبت به ظرفیت وسایل حمل‌ونقل و تحلیل حساسیت نسبت به شعاع پوششی پایگاه‌های امداد. برای بررسی تأثیر ظرفیت حمل تیم‌های امداد، سناریوهایی با افزایش و کاهش درصدی ظرفیت وسایل نقلیه در مدل اجرا شد. با تغییر شعاع پوششی پایگاه‌ها، تغییرات در پوشش‌دهی، تعداد پایگاه‌های موردنیاز و الگوی مسیریابی بررسی شد. 

تحلیل حساسیت مسئله از‌نظر ظرفیت وسایل حمل‌و‌نقل 
در این قسمت تحلیل حساسیت بر روی مثال 5 جدول شماره 7 انجام می‌شود. در هر مرحله از وسایل نقلیه بزرگ‌تر و با ظرفیت بیشتر و بالطبع دارای هزینه به‌کارگیری بیشتر استفاده می‌شود. از‌آنجایی‌که شکست تقاضا در هر دو سطح مجاز نیست باید وسایل نقلیه سطح اول به‌گونه‌ای انتخاب شوند که ظرفیت آن‌ها بزرگ‌تر یا مساوی با حداکثر مقدار تقاضای امدادی تخصیص‌یافته به پایگاه‌های امداد و کوچک‌تر یا مساوی با حداقل ظرفیت پایگاه‌های امداد باشند. همچنین ظرفیت هر وسیله نقلیه سطح دوم باید بزرگ‌تر یا مساوی با حداکثر مقدار تقاضای امدادی نقاط حادثه‌دیده باشد. برای این مثال حداکثر تقاضای نقاط حادثه‌دیده برابر 5 واحد و حداکثر تقاضای تخصیص‌یافته به پایگاه‌های امداد برابر 15 واحد است. بنابراین برای سطح اول باید از وسایل نقلیه‌ای با حداقل ظرفیت 15 و برای سطح دوم از وسایل نقلیه‌ای با حداقل ظرفیت 5 استفاده کرد.  ظرفیت وسایل نقلیه سطح اول،  ظرفیت وسایل نقلیه سطح دوم، هزینه ثابت استفاده از وسایل نقلیه سطح اول و  هزینه ثابت استفاده از وسایل نقلیه سطح دوم است. در ابتدا تحلیل حساسیت مسئله از‌نظر ظرفیت وسایل حمل‌و‌نقل سطح اول و سپس برای سطح دوم انجام گرفته است. همان‌گونه که در جداول شماره 8 و 9 مشاهده می‌شود استفاده از وسایل نقلیه با ظرفیت بیشتر باعث کاهش تعداد وسایل استفاده‌شده و در‌نهایت کاهش هزینه امداد‌رسانی به نقاط آسیب‌دیده شده است.




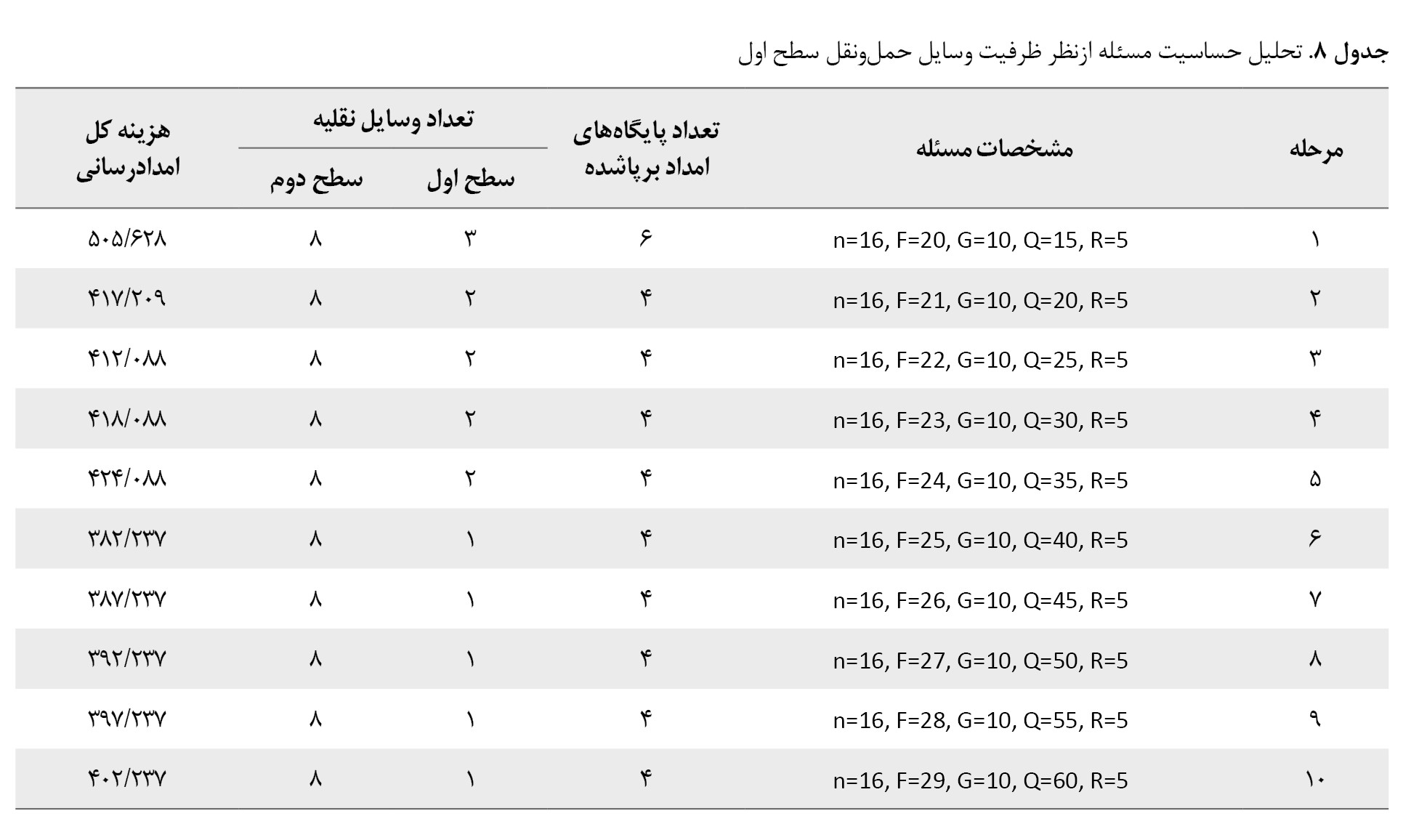
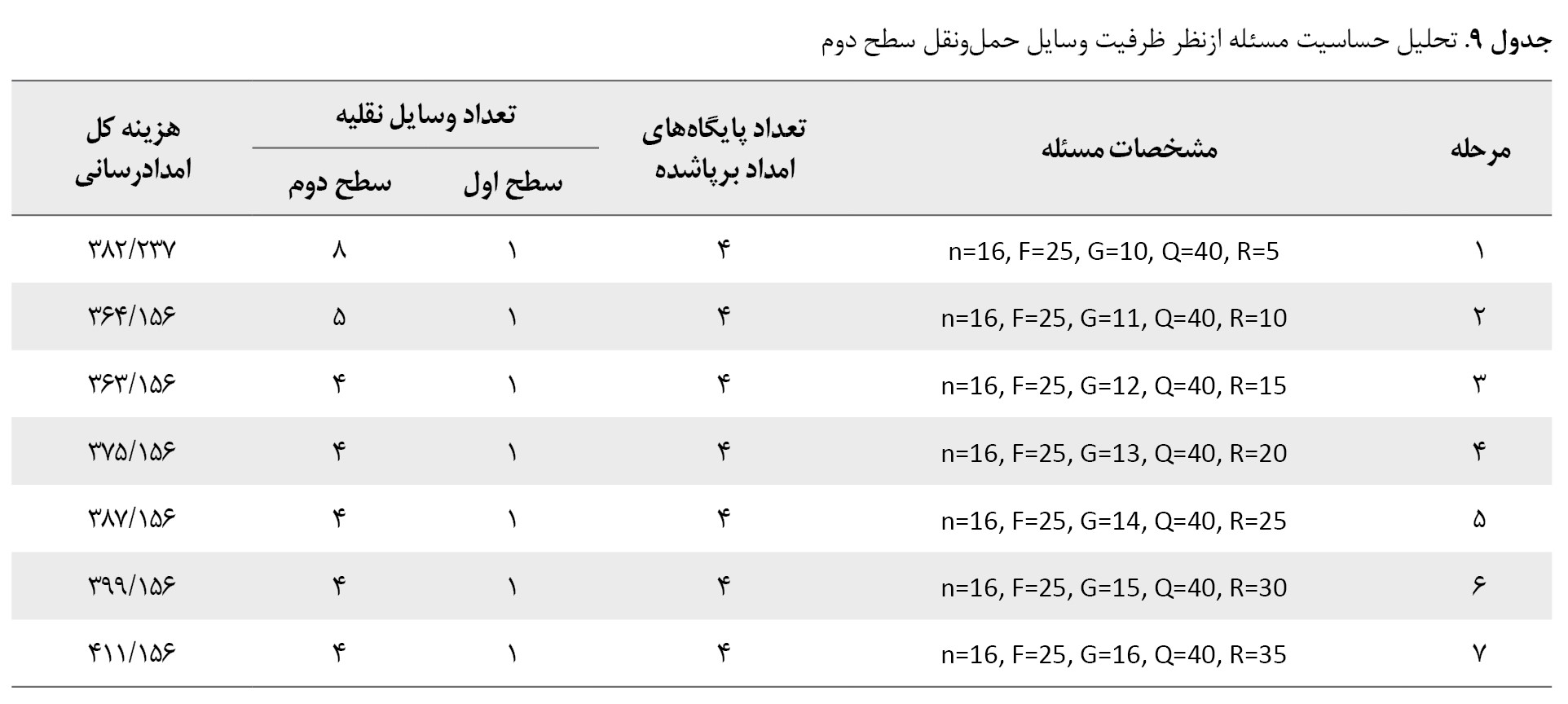
اما باید دقت شود که لزوماً استفاده از وسایل نقلیه با ظرفیت زیاد همواره باعث کاهش هزینه‌ها نمی‌شود. به‌عنوان مثال بزرگ‌ترین وسیله نقلیه‌ای که می‌تواند برای سطح اول به‌کار گرفته شود وسیله نقلیه‌ای با حداکثر ظرفیت برابر با کل مقدار تقاضای امدادی نقاط حادثه‌دیده است. برای این مثال بهترین وسایل حمل‌و‌نقل سطح اول در مرحله 6 جدول شماره 8 و برای سطح دوم در مرحله 3 جدول شماره 9 به دست آمده است. نتایج در جدول شماره 8 آورده شده‌اند.

تحلیل حساسیت مسئله از‌نظر شعاع پوششی پایگاه‌های امداد
تحلیل حساسیت مسئله 2E-RCTLRP از‌نظر شعاع پوششی پایگاه‌های امداد برای مثال 4 جدول شماره 7 انجام می‌شود. بدین منظور شعاع پوشش پایگاه‌ها در هر مرحله به‌صورت تصادفی افزایش داده می‌شود تا اینکه در‌نهایت شعاع پوشش حداکثر شود. شعاع پوشش حداکثر برای یک پایگاه امداد برابر با بیشترین فاصله نقاط حادثه‌دیده از آن پایگاه است. شعاع پوششی مرحله اول برابر با حداقل شعاعی است که همه نقاط حادثه‌دیده توسط پایگاه‌های امداد پوشش یابند. تمامی مشخصات پایگاه‌های امداد و وسایل نقلیه استفاده‌شده در تمامی مراحل تحلیل حساسیت و مسئله 2E-LRP یکسان در نظر گرفته شده‌اند. نتایج این تحلیل حساسیت در جدول شماره 10 آمده است.


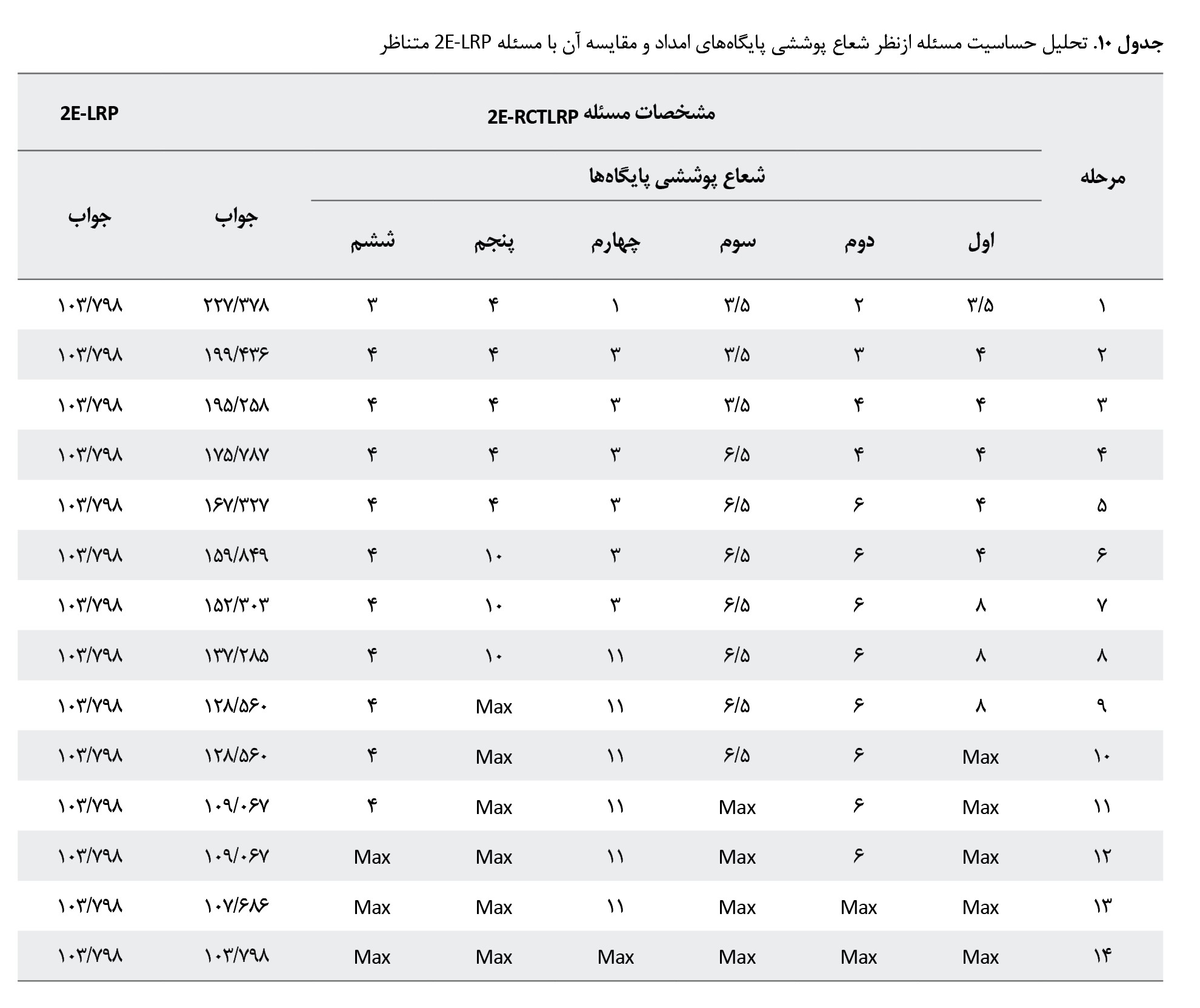
با مشاهده این جدول می‌توان نتیجه گرفت با افزایش شعاع پوشش پایگاه‌های امداد، مسئله 2E-RCTLRP با مسئله 2E-LRP همگرا می‌شود.

مقایسه حل مسئله 2E-RCTLRP با 2E-LRP ،‌LRP و CTP متناظر
در این قسمت جواب مثال‌های از نوع 2E-RCTLRP با مثال‌های متناظر از نوع 2E-LRP، LRP و CTP مقایسه شده است. در همه مثال‌ها ظرفیت وسایل نقلیه، هزینه ثابت استفاده از وسایل نقلیه و هزینه برپایی پایگاه‌های امداد یکسان در نظر گرفته شده است. در مسئله LRP یک سطحی تعریف شده و امداد‌رسانی از پایگاه مرکزی امداد به نقاط حادثه‌دیده با استفاده از وسایل نقلیه موجود در پایگاه مرکزی امداد صورت گرفته است. در مسئله CTP، 1 سطحی تعریف‌شده، پایگاه‌های امداد توسط پایگاه مرکزی امداد تجهیز می‌شوند و سپس افراد حادثه‌دیده جهت دریافت خدمات امداد به پایگاه‌های برپا‌شده مراجعه می‌کنند. بنابراین چون افراد مستقیماً امدادرسانی نمی‌شوند هزینه‌ای به مدل اضافه شده است. از آنجایی‌که برای مسئله 2E-RCTLRP محدودیت پوشش برای پایگاه‌های امداد در نظر گرفته شده است، هزینه این مثال‌ها از مثال‌های مربوط به 2E-LRP بیشتر شده است که این اختلاف به معنای برتری 2E-LRP نسبت به 2E-RCTLRP نیست. نتایج حل مثال‌ها در جدول شماره 11 و تصویر شماره 5 زیر آورده شده است.

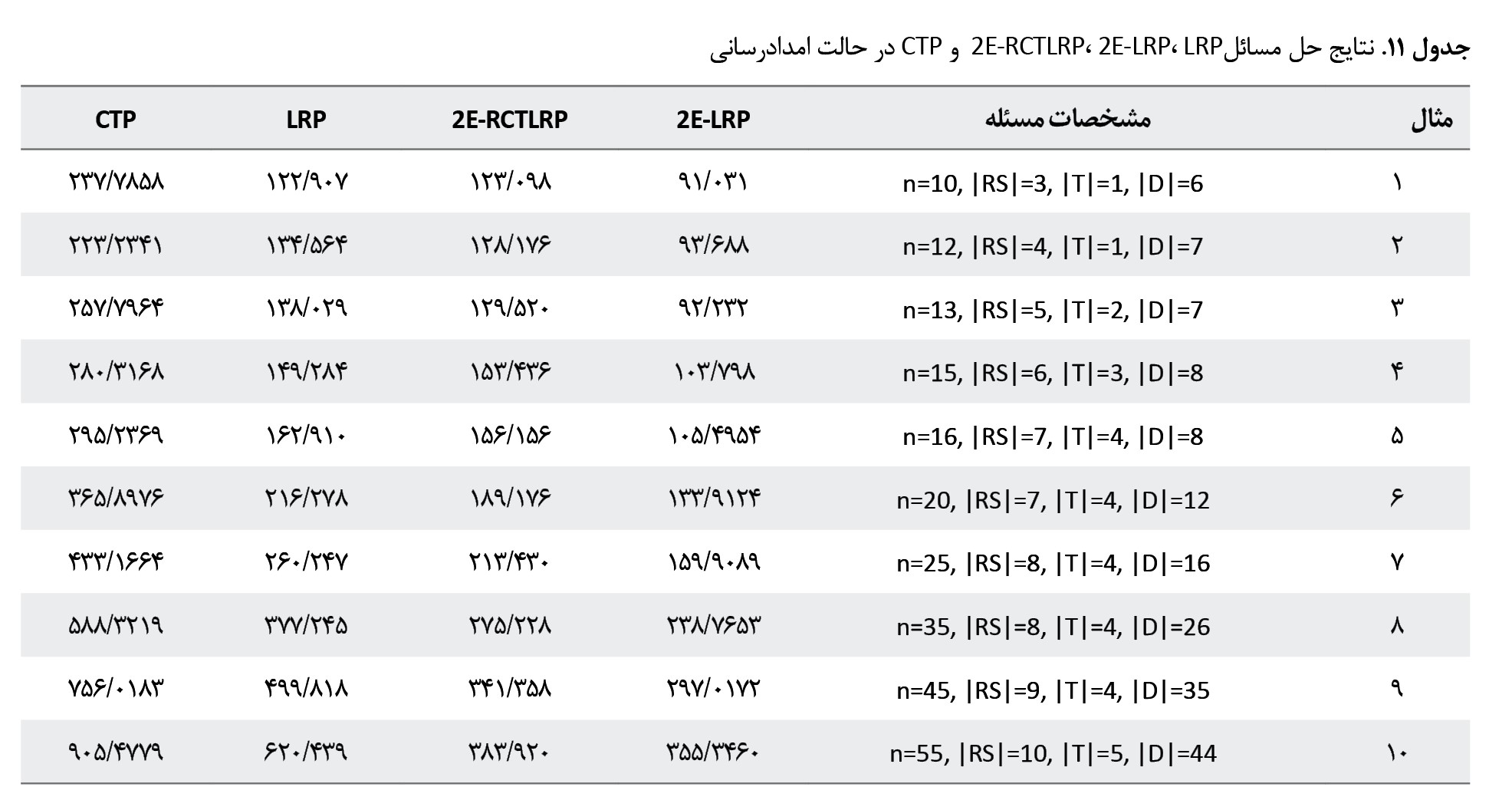
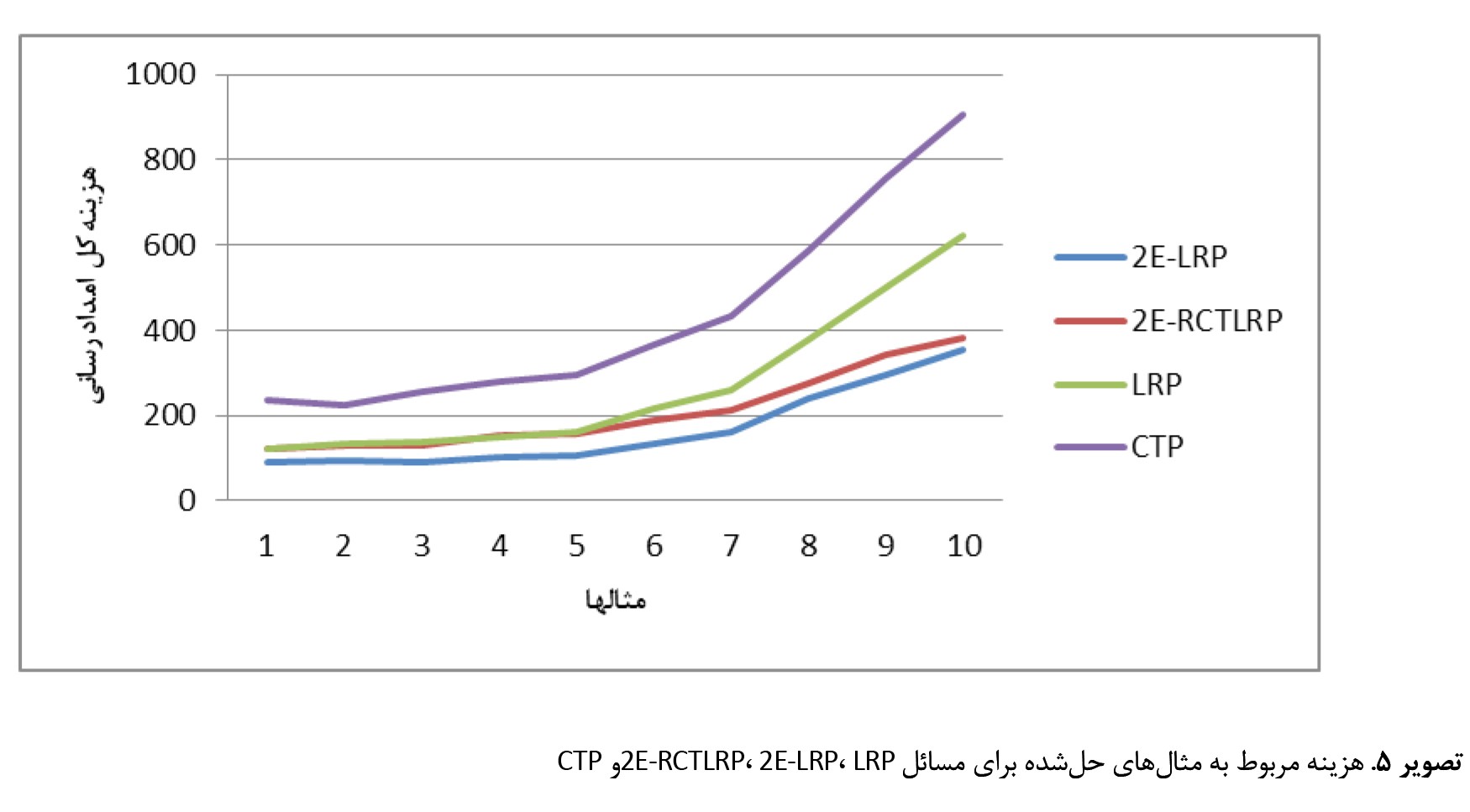
همان‌گونه که پیداست روش‌های 2 سطحی به‌مراتب نتایج بهتری نسبت به روش‌های تک‌سطحی ارائه می‌دهند. 

نتیجه‌گیری
بر اساس بررسی‌های صورت‌گرفته به نظر می‌رسد، پژوهش حاضر نوآوری‌های قابل‌توجهی را در دو بُعد اصلی ارائه می‌دهد: نخست، «در این تحقیق، برای نخستین‌بار مدلی دو‌سطحی از مسئله مکان‌یابی–مسیریابی ارائه شده است که هم‌زمانی تشکیل تورها در هر دو سطح را در قالب تورهای پوششی با شعاع متغیر پوشش پایگاه‌های امداد در نظر می‌گیرد. این مدل، برخلاف بسیاری از پژوهش‌های پیشین که با فرض شعاع ثابت پوشش، ساختار تک‌سطحی و بی‌توجهی به هم‌زمانی تورها همراه بوده‌اند، به واقعیت‌های پیچیده شرایط بحران و امدادرسانی نزدیک‌تر است.» دوم، مدل پیشنهادی با در نظر گرفتن تفاوت در ظرفیت و میزان آسیب‌دیدگی شهرها، امکان تصمیم‌گیری هوشمندانه‌تر در مکان‌یابی پایگاه‌ها را فراهم می‌آورد. درحالی‌که در اغلب مطالعات گذشته این متغیرها یا لحاظ نشده‌اند یا به شکل ساده‌شده مدل‌سازی شده‌اند. حال آنکه طراحی یک شبکه امداد‌رسانی دو سطحی می‌تواند سرعت و کیفیت امداد‌رسانی در شرایط بحران را افزایش دهد. در این تحقیق در ابتدا مسئله امداد‌رسانی تور پوششی دو سطحی تعریف، مدل‌سازی و سپس حل شد. نتایج حاصل از حل مسئله نشان می‌دهد الگوریتم ژنتیک پیشنهادی، الگوریتمی کارا و کاربردی است. در حل تمام مثال‌ها، تورهای هر دو سطح به‌طور هم‌زمان تشکیل شده‌اند. با ارائه مثالی نشان داده شده است که نتایج حل حاصل از تشکیل تورهای دو سطح به‌صورت هم‌زمان و غیرهم‌زمان متفاوت است و حل مسئله با در نظر گرفتن تشکیل هم‌زمانی تورها در هر دو سطح دارای نتایج بهتری است. در ادامه به تحلیل حساسیت مسئله از‌نظر ظرفیت وسایل حمل‌و‌نقل پرداخته و نتیجه‌گیری شد افزایش ظرفیت وسایل حمل‌و‌نقل معمولاً باعث کاهش هزینه امداد‌رسانی می‌شود، اما باید دقت شود لزوماً استفاده از وسایل نقلیه با ظرفیت بیشتر همواره باعث کاهش هزینه‌ها نمی‌شود و باید وسیله حمل‌و‌نقل با ظرفیت بهینه استفاده شود. همچنین با افزایش شعاع پوششی پایگاه‌های امداد، مسئله مورد‌تحقیق با مسئله 2E-LRP همگرا می‌شود و نهایتاً مقایسه‌ای بین مسائل 1 سطحی و 2 سطحی در شرایط امداد انجام گرفت و نتیجه‌گیری شد روش‌های دو سطحی به مراتب نتایج بهتری نسبت به روش‌های تک‌سطحی ارائه می‌دهند.
الگوریتم ژنتیک به‌عنوان یک روش فراابتکاری، در حل مسائل پیچیده و با ابعاد بزرگ، مانند مسئله تور پوششی 2 سطحی در شرایط امدادرسانی، دارای مزایای قابل‌توجهی است. یکی از مهم‌ترین نقاط قوت این الگوریتم، توانایی آن در جست‌وجوی گسترده و متنوع در فضای پاسخ است، به‌گونه‌ای که با بهره‌گیری از یک جمعیت از راه‌حل‌ها، امکان اکتشاف هم‌زمان در نواحی مختلف فضای جست‌وجو فراهم می‌شود. این ویژگی باعث افزایش احتمال یافتن پاسخ‌های بهتر و کاهش خطر گیر افتادن در بهینه‌های محلی می‌شود. همچنین الگوریتم ژنتیک به دلیل ساختار جمعیتی و مبتنی بر تکامل خود، برای مسائل بزرگ‌مقیاس که در آن‌ها روش‌های دقیق از‌نظر زمانی یا محاسباتی ناکارآمد هستند، گزینه‌ای مناسب محسوب می‌شود. افزون بر این، انعطاف‌پذیری بالای الگوریتم ژنتیک در انطباق با انواع مختلف توابع هدف و قیود، آن را به ابزاری قدرتمند در شرایط متغیر و پویای مسئله، به‌ویژه در حوزه امدادرسانی، تبدیل کرده است. با‌این‌حال استفاده از الگوریتم ژنتیک با برخی محدودیت‌ها نیز همراه است. از‌جمله، این الگوریتم تضمینی برای دستیابی به جواب بهینه مطلق ندارد و معمولاً تنها راه‌حل‌های تقریباً بهینه را ارائه می‌دهد که در برخی کاربردها ممکن است ناکافی باشد. همچنین عملکرد الگوریتم به‌شدت وابسته به تنظیم مناسب پارامترهایی، مانند اندازه جمعیت، نرخ تقاطع و نرخ جهش استو انتخاب نادرست این پارامترها می‌تواند منجر به هم‌گرایی زودهنگام یا کاهش کیفیت پاسخ شود. از سوی دیگر، به‌ویژه در مسائل بزرگ، الگوریتم ژنتیک ممکن است برای دستیابی به پاسخ‌های قابل‌قبول، به زمان محاسباتی قابل‌توجهی نیاز داشته باشد که این امر در مقایسه با برخی روش‌های فراابتکاری دیگر، می‌تواند به‌عنوان یک نقطه ضعف تلقی شود.
 در نظر گرفتن شعاع پوشش متغیر برای هر پایگاه امداد، استفاده از وسایل حمل‌و‌نقل متفاوت در هر سطح و همچنین بررسی مسئله در حالت پوشش حداکثر به‌منظور کاهش زمان امداد‌رسانی می‌توانند به‌عنوان موضوع مطالعات آتی در این حوزه پیشنهاد شوند. همچنین استفاده از داده‌های واقعی در مدل‌سازی یا مقایسه الگوریتم ژنتیک با سایر روش‌های بهینه‌سازی می‌تواند به‌عنوان زمینه‌ای برای تحقیقات آتی مطرح شود.

ملاحظات اخلاقی
پیروی از اصول اخلاق پژوهش
در این مطالعه تمام اصول اخلاقی رعایت شد. ازآنجایی‌که هیچ آزمایشی بر روی نمونه‌های انسانی یا حیوانی انجام نشد، نیازی به رعایت اصول اخلاقی نبود.

حامی مالی
این پژوهش هیچ‌گونه کمک مالی از سازمانی‌های دولتی، خصوصی و غیرانتفاعی دریافت نکرده است.

مشارکت نویسندگان
همه نویسندگان به‌طور یکسان در مفهوم و طراحی مطالعه، جمع‌آوری و تجزیه‌وتحلیل داده‌ها، تفسیر نتایج و تهیه پیش‌نویس مقاله مشارکت داشتند.

تعارض منافع
بنابر اظهار نویسندگان، این مقاله تعارض منافع ندارد.

References
Allahyari, S., Salari, M., & Vigo, D. (2015). A hybrid metaheuristic algorithm for the multi-depot covering tour vehicle routing problem. European Journal of Operational Research, 242(3), 756-768. [DOI:10.1016/j.ejor.2014.10.048] 
Altay, N., & Green III, W. G. (2006). OR/MS research in disaster operations management. European Journal of Operational Research, 175(1), 475-493. [DOI:10.1016/j.ejor.2005.05.016] 
Arkin, E. M., & Hassin, R. (1994). Approximation algorithms for the geometric covering salesman problem. Discrete Applied Mathematics, 55(3), 197-218. [DOI:10.1016/0166-218X(94)90008-6] 
Belenguer, J., Benavent, E., Prins, C., Prodhon, C., & Woler Calvo, R. (2011). A branch-and-cut method for the capacitated location-routing problem. Computers and Operations Research, 38(6), 931-941. [DOI:10.1016/j.cor.2010.09.019] 
Boccia, M., Crainic, T. G., Sforza, A., & Sterle, C. (2010). A metaheuristic for a two echelon location-routing problem. In P. Festa (Ed.), Experimental Algorithms. SEA 2010. Lecture Notes in Computer Science, vol 6049. Berlin: Springer. [DOI:10.1007/978-3-642-13193-6_25] 
Bottani, E., Casella, G., & Murino, T. (2021). A hybrid metaheuristic routing algorithm for low-level picker-to-part systems. Computers & Industrial Engineering, 160, 107540. [DOI:10.1016/j.cie.2021.107540]
Cai, Z., Mo, D., Geng, M., Tang, W., & Chen, X. M. (2023). Integrating ride-sourcing with electric vehicle charging under mixed fleets and differentiated services. Transportation Research Part E: Logistics and Transportation Review, 169, 102965.  [DOI:10.1016/j.tre.2022.102965]
Caunhye, A. M., Nie, X., & Pokharel, S. (2012). Optimization models in emergency logistics: A literature review. SocioEconomic Planning Sciences, 46(1), 4-13. [DOI:10.1016/j.seps.2011.04.004]
Choi, J., Lee, S., & Choi, H. (2022). The influence of knowledge, trust, and perceived risk on firefighters’ preparedness and willingness to respond to nuclear emergencies: The case of South Korea. International Journal of Disaster Risk Science, 13, 536–548. [Link]
Contardo, C., Cordeau, J. F., & Gendron, B. (2013). A computational comparison of flow formulations for the capacitated location-routing problem. Discrete Optimization, 10(4), 263-295. [DOI:10.1016/j.disopt.2013.07.005] 
Contardo, C., Hemmelmayr, V., & Crainic, T. G. (2012). Lower and upper bounds for the two-echelon capacitated location-routing problem. Computers & Operations Research, 39(12), 3185–3199. [DOI:10.1016/j.cor.2012.04.003] [PMID]  
Crainic, T. G., Sforza, A., & Sterle, C. (2011a). Tabu search heuristic for a two-echelon location-routing problem. Quebec: Cirrelt. [Link]
Crainic, T. G., Sforza, A., & Sterle, C. (2011b). Location-routing models for two-echelon freight distribution system design. Quebec: Cirrelt. [Link]
Current, J. R. , & Schilling, D. A. (1989). The covering salesman problem. Transportation Science, 23(3), 208-213. [DOI:10.1287/trsc.23.3.208] 
De La Torre, L. E., Dolinskaya, I. S., & Smilowitz, K. R. (2012). Disaster relief routing: Integrating research and practice. Socio-Economic Planning Sciences, 46(1), 88-97. [DOI:10.1016/j.seps.2011.06.001] 
Doerner, K., Focke, A., & Gutjahr, W. J. (2007). Multicriteria tour planning for mobile healthcare facilities in a developing country. European Journal of Operational Research, 179(3), 1078-1096. [DOI:10.1016/j.ejor.2005.10.067] 
Dalal, J., & Üster, H. (2019). Combining worst-case and average-case considerations in an integrated emergency response network design problem. Transportation Science, 52(1), 52–67. [DOI:10.1287/trsc.2016.0725]
Gendreau, M., Laporte, G., & Semet, F. (1997). The covering tour problem. Operations Research, 45(4), 568-576. [DOI:10.1287/opre.45.4.568] 
Golden, B., Naji-Azimi, Z., Raghavan, S., Salari, M., & Toth, P. (2012).The generalized covering salesman problem. INFORMS Journal on Computing, 24(4), 534-553. [DOI:10.1287/ijoc.1110.0480] 
Golden, B. L., Raghavan, S., & Wasil, E. A. (2008). The vehicle routing problem: Latest advances and new challenges. Berlin: Springer. [Link]  
Govindan, K., Jafarian, A., Khodaverdi, R., & Devika, K. (2013). Two-Echelon Multiple-Vehicle Location-Routing Problem with Time Windows for optimization of sustainable supply chain network of perishable food. International Journal of Production Economics,152, 9-28. [DOI:10.1016/j.ijpe.2013.12.028] 
Hachicha, M., Hodgson, M. J., Laporte, G., & Semet, F. (2000). Heuristics for the multi-vehicle covering tour problem. Computers & Operations Research, 27(1), 29-42. [DOI:10.1016/S0305-0548(99)00006-4] 
Han, C. F., & Zhang, C. (2009). Genetic algorithm for solving problems in emergency management. Paper presented at: 2009 Fifth International Conference on Natural Computation,Tianjian, China, 14-16 August 2009. [DOI:10.1109/ICNC.2009.333] 
Hodgson, M. J., Laporte, G., & Semet, F. (1998). A covering tour model for planning mobile health care facilities in SuhumDistrict, Ghama. Journal of Regional Science, 38(4), 621-638. [Link]
Jacobsen, S. K., & Madsen, O. B. G. (1980). A comparative study of heuristics for a two-level routing-location problem. European Journal of Operational Research, 5(6), 378-387. [DOI:10.1016/0377-2217(80)90124-1] 
Jang, H. C., Lien, Y. N., & Tsai, T. C. (2009, June). Rescue information system for earthquake disasters based on MANET emergency communication platform. Proceedings of the 2009 International Conference on Wireless Communications and Mobile Computing: Connecting the World Wirelessly, 623-627. [DOI:10.1145/1582379.1582514] 
Jamali, H. , Bashiri, M., & Tavakkoli-Moghaddam, R. (2016). [Modeling and a genetic algorithm for the two-echelon relief logistics problem (Persian)]. Emergency Management, 4(2), 5-22. [Link]
Jamali, H, Bashiri, M, & Tavakoli Moghadam, R. (2015). [Management of relief operations in emergency situations using the concept of cover tour and the possibility of sending(Persian)]. Modiriat-e- Farda, 42(14), 1-10. [Link]
Jamali, H., & Bashiri, M. (2020). [Modeling for the Covering Tour Problem in Relief Condition for Disaster Management (Persian)]. Emergency Management, 9(1), 69-82. [Link]
Jebbor, S., Raddouane, C., & El Afia, A. (2022). A preliminary study for selecting the appropriate AI-based forecasting model for hospital assets demand under disasters. Journal of Humanitarian Logistics and Supply Chain Management, 12 (1), pp. 1-29. [DOI:10.1108/JHLSCM-12-2020-0123]
Jiao, L., Peng, Z., Xi, L., Guo, M., Ding, S., & Wei, Y. (2023). A multi-stage heuristic algorithm based on task grouping for vehicle routing problem with energy constraint in disasters. Expert Systems with Applications, 212, 118740. [DOI:10.1016/j.eswa.2022.118740]
Khanna, R., Konyukhov, Y. V., Burmistrov, I., Cayumil, R., Belov, V. A., & Rogachev, S. O., et al. (2021). An innovative route for valorising iron and aluminium oxide rich industrial wastes: Recovery of multiple metals. Journal of Environmental Management, 295, 113035. [DOI:10.1016/j.jenvman.2021.113035]
Liu, W., Li, J., & Xu, J. (2020). Effects of disaster-related resettlement on the livelihood resilience of rural households in China. International Journal of Disaster Risk Reduction, 49, 101649. [DOI:10.1016/j.ijdrr.2020.101649]
Malikov, E., Zhang, J., Zhao, S., & Kumbhakar, S. C. (2022). Accounting for cross-location technological heterogeneity in the measurement of operations efficiency and productivity. Journal of Operations Management, 68(2), 153-184. [Link]
Madsen, O. B. G. (1983). Methods for solving combined two-level location-routing problems of realistic dimensions. European Journal of Operational Research, 12(3), 295-301. [DOI:10.1016/0377-2217(83)90199-6] 
Mohamad, F. A., Rezapour, S., Baghaian, A., & Amini, M. H. (2023). An integrative framework for coordination of damage assessment, road restoration, and relief distribution in disasters. Omega, 115, 102748. [DOI:10.1016/j.omega.2022.102748]
Nagy, G., & Salhi, S. (1996). Nested heuristics methods for the location-routing problem. Journal of Operational Research Society, 47(9), 1166-1174. [DOI:10.1057/jors.1996.144] 
Naji-Azimi, Z., Renaud, J., Ruiz, A. , & Salari, M. (2012). A covering tour approach to the location of satellite distribution centers to supply humanitarian aid. European Journal of Operational Research, 222(3), 596-605. [DOI:10.1016/j.ejor.2012.05.001] 
Nguyen, V.P., Prins, C., & Prodhon, C. (2012a). Solving the two-echelon location routing problem by a GRASP reinforced by a learning process and path relinking. European Journal of Operational Research, 216(1), 113-126. [DOI:10.1016/j.ejor.2011.07.030] 
Nguyen, V. P., Prins, C., & Prodhon, C. (2012b).A multi-start iterated local search with tabu list and path relinking for the two-echelon location-routing problem. Engineering Applications of Artificial Intelligence, 25(1), 56-71. [DOI:10.1016/j.engappai.2011.09.012] 
Nolz, P. C., Doerner, K.F., Gutjahr, W. J., & Hartl, R. F. (2010). A bi-objective metaheuristic for disaster relief operation planning. In C. A. Coello Coello, C. Dhaenens & L. Jourdan, (Eds), Advances in Multi-Objective Nature Inspired Computing. Studies in Computational Intelligence, vol 272. Berlin: Springer. [DOI:10.1007/978-3-642-11218-8_8] 
Oliveira, B., Pessoa, A. & Roboredo, M. (2025). New cuts and a branch-cut-and-price model for the multi-vehicle covering tour problem. 4OR: A Quarterly Journal of Operations Research. [DOI:10.1007/s10288-025-00584-0] 
Pashapour, A., Günneç, D., Salman, F. S., & Yücel, E. (2024). Capacitated mobile facility location problem with mobile demand: Efficient relief aid provision to en route refugees. Omega, 129, 103138. [DOI:10.1016/j.omega.2024.103138] 

 
Pirkwieser, S., & Raidl, G. R. (2010). Variable neighborhood search coupled with ILP-based very large neighborhood searches for the (periodic) location-routing problem. In M. J. Blesa, C. Blum,  G. Raidl, A. Roli & M. Sampels(Eds.), Hybrid Metaheuristics. HM 2010. Lecture Notes in Computer Science, vol 6373. Berlin: Springer. [DOI:10.1007/978-3-642-16054-7_13]
Rath, S., & Gutjahr, W.J. (2014). A math-heuristic for the warehouse location-routing problem in disaster relief. Computers and Operations Research, 42, 25-39. [DOI:10.1016/j.cor.2011.07.016] 
Schwengerer, M., Pirkwieser, S., & Raidl, G. R. (2012). A variable neighborhood search approach for the two-echelon location-routing problem. In J. K. Hao & M. Middendorf (Eds.), Evolutionary Computation in Combinatorial Optimization. EvoCOP 2012. Lecture Notes in Computer Science, vol 7245 (pp.13-24). Berlin: Springer.  [DOI:10.1007/978-3-642-29124-1_2] 
Tarhan, İ., Zografos, K. G., Sutanto, J., & Kheiri, A. (2023). A quadrant shrinking heuristic for solving the dynamic multi-objective disaster response personnel routing and scheduling problem. European Journal of Operational Research, 314(2), 776–791. [DOI:10.1016/j.ejor.2023.09.002]
Tuzun, D., & Burke, L. I. (1999). A two-phase tabu search approach for the location routing problem. European Journal of Operational Research, 116, 87-99. [DOI:10.1016/S0377-2217(98)00107-6] 
Wang, H., Du, L., & Ma, Sh. (2014). Multi-objective open location-routing model with split delivery for optimized relief distribution in post-earthquake. Transportation Research Part E: Logistics and Transportation Review, 69, 160-179. [DOI:10.1016/j.tre.2014.06.006] 
Wang, D. W., & Zhang, G. X. (2005). Model and algorithm to optimize location of catastrophic rescue center. Journal of Northeastern University (Natural Science), 26(10), 953-956. [Link]
Yi, W., & Özdamar, L. (2007). “A dynamic logistics coordination model for evacuation and support in disaster response activities.European Journal of Operational Research, 179(3), 1177-1193. [DOI:10.1016/j.ejor.2005.03.077] 
Zegordi, S. H., & Nikbakhsh, E. (2010). A heuristic algorithm and a lower bound for the two-echelon location-routing problem with soft time window constraints. Scientia Iranica, 17(1), 36-47. [Link]
Zhang, N., Ou, M., Liu, B., & Liu, J. (2023). A GERT network model for input-output optimization of general aviation industry chain based on value flow. Computers & Industrial Engineering, 176, 108945. [DOI:10.1016/j.cie.2022.108945] 
Zhu, Q., Chen, J. M., Tseng, M. L., & Luan, H. M. (2020). Modelling green multimodal transport route performance with Witness simulation software. Journal of Cleaner Production, 248, 119245. [DOI:10.1016/j.jclepro.2019.119245]