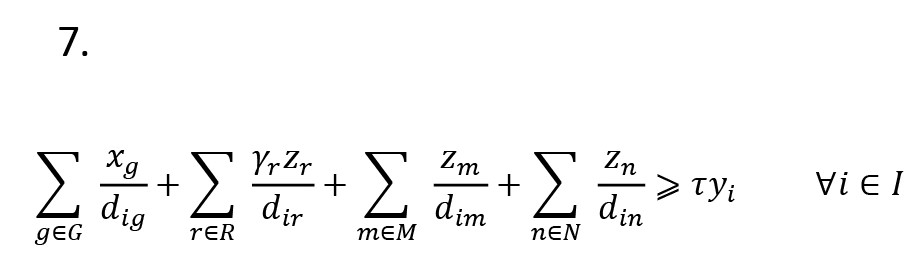مقدمه
هدف از انجام این پژوهش، ارائه مدلی بر‌اساس نظریه بازی است که همکاری اهداکنندگان، سازمان‌های بشردوستانه، دولت و سازمان‌های بخش خصوصی را بررسی کند. این مدل به‌منظور اطمینان حاصل کردن از ارائه پوشش حداکثری به نقاط آسیب‌دیده طراحی شده است و به تنوع بازیکنان و ابعاد فاجعه توجه دارد.
در این پژوهش، اصطلاحات کلیدی، شامل «زنجیره تأمین بشردوستانه»، «نظریه بازی»، «همکاری» و «مدیریت بحران» به کار رفته است. زنجیره تأمین بشردوستانه به شبکه‌ای از سازمان‌ها اشاره دارد که در زمان وقوع فجایع برای ارائه کمک‌های انسانی همکاری می‌کنند. نظریه بازی به تحلیل تعاملات استراتژیک بین این سازمان‌ها کمک می‌کند.
فجایع و مخاطرات طبیعی و انسانی در صورت وقوع، اثرات و تبعات بلندمدت و منفی و گاه جبران‌ناپذیری دارند. در سراسر دنیا و همچنین در ایران، پاسخ به چنین اتفاقاتی نیازمند داشتن مدیریت مؤثر در فراهم کردن کمک‌رسانی درست است. پس از وقوع فجایع با ابعاد بسیار گسترده در دنیا، مانند طوفان کاترینا در 2005 و زلزله هائیتی در سال 2010 توجه بسیاری از محققان به توسعه مدل‌های نظریه بازی جهت بررسی مدیریت هرچه بهتر چنین عملیات‌هایی جلب شد و نیاز به توسعه مفهوم زنجیره تأمین بشردوستانه اجتناب‌ناپذیر شد. از عوامل تعیین‌کننده در کیفیت و عملکرد بهینه زنجیره تأمین بشردوستانه، همکاری و اقدام مؤثر و به‌موقع طرفین درگیر در این زنجیره است. از بازیکنان تأثیرگذار در چنین عملیات‌هایی، سازمان‌های بشردوستانه و کمک‌رسان، اهداکنندگان آنان و دولت هستند. دولت‌ها یا با ارائه کالا به‌صورت مستقیم و یا از‌طریق سپردن انواع مختلف کمک اعم از کالا و مالی به سازمان‌های بشردوستانه، به آسیب‌دیدگان فاجعه کمک می‌کنند (فتحعلیخانی و همکاران، 2018). 
ازطرف‌دیگر، سازمان‌های بشردوستانه بنا برحیطه فعالیت خود، محل دریافت کمک‌های اهداکنندگان هستند و بایستی با عملکرد درست و مؤثر، اعتماد این حامیان را جلب کرده و نگه دارند. در جهت تلاش برای این اعتمادسازی و نگهداری آن، تلاش برای آمادگی و برنامه‌ریزی برای زمان وقوع فجایع احتمالی بیشتر حائز اهمیت می‌‌شود. یکی از راهکارهای بالا بردن عملکرد و سرعت و بهبود مدیریت در زنجیره تأمین‌های اضطراری و بشردوستانه، بهره‌گیری از ظرفیت‌های سازمان‌های مربوط به بخش خصوصی است (چن و همکاران، 2013). با در نظر گرفتن تعدد ذی‌نفعان معرفی‌شده و انگیزه‌های گوناگون و اهداف آنان، دور از ذهن نیست که مسئله بررسی ارتباطات و انگیزه‌های همه طرفین در کنار هم مطرح شود تا از وجود امکان و آمادگی لازم برای همکاری تمامی ذی‌نفعان برای نیل به هدف مشترک که کمک‌رسانی و فراهم کردن حداکثری کمک به آسیب‌دیدگان هر فاجعه است اطمینان حاصل شود.

پیشینه پژوهش
برای بررسی ارتباط و انگیزه بازیکنان مذکور، در طول سال‌های گذشته پژوهش‌های متعددی با تکیه بر مدل‌های نظریه بازی ‌ارائه شده‌اند (ماگی و همکاران، 2014؛ آلداشِو، 2010). یک مدل رقابتی که بر جمع‌آوری کمک مالی بین سازمان‌های غیردولتی تمرکز دارد ارائه شد. سازمان‌های غیردولتی عموماً زمان خود را به کار روی پروژه‌ها و همچنین جمع‌آوری کمک‌های مالی اختصاص می‌دهند که کمک‌های مالی خصوصی را جذب می‌کند. بر‌اساس این مدل، اگر اندازه بازار ثابت باشد، سطوح جذب سرمایه با تعداد سازمان‌های غیردولتی افزایش می‌یابد و بسته به کارایی فناوری جمع‌آوری سرمایه، عدد تعادل ورود آزاد سازمان‌های غیردولتی می‌تواند بزرگ‌تر یا کوچک‌تر از تعداد بهینه از‌نظر اجتماعی باشد. ژانگ و همکاران (2014) با استفاده از نظریه بازی، به بررسی اثر افشای اطلاعات به جلب سرمایه از اهداکنندگان پرداختند. در این تحقیق، یک مدل بر‌اساس نظریه بازی جهت تحلیل تعاملات افشا ـ اهدا ارائه شد. 
کُلز و ژوانگ (2011) تصمیم‌گیری و همکاری در طی عملیات‌های کمک‌رسانی را با استفاده از مفاهیم نظریه بازی بررسی کردند. با استفاده از تئوری بازی، یک رویکرد اولیه برای توسعه یک چارچوب پشتیبانی تصمیم برای مدیران اضطراری که وارد یک محیط فاجعه می‌شوند، ارائه شد و رویکردی برای حمایت و راهنمایی تصمیم‌گیرندگان در محیط‌های اضطراری در‌مورد چگونگی انتخاب و توسعه روابط برای بهبود استفاده از منابع و نتایج پروژه در پی یک فاجعه پیشنهاد شد. 
دِی و همکاران (2012) به بررسی اهمیت و ویژگی‌های زنجیره تأمین کمک‌رسانی و امور بشردوستانه پرداختند. در این تحقیق فعالیت‌هایی مانند تعیین تقاضا، هماهنگی زنجیره تأمین، تشخیص زمان حرکت در طول چرخه حیات و بازسازی پس از فاجعه را توصیف شد که چالش‌های زنجیره تأمین را از چالش‌های لجستیک متمایز می‌کنند. 
شولتز و بلکن (2010) استفاده از ظرفیت‌های بخش خصوص در زمان بحران و پس از وقوع فاجعه را مورد توجه قرار دادند. همکاری بخش اضطراری، حاکی از همکاری کوتاه‌مدت بین بخش خصوصی و دولتی است و تنها برای رسیدگی به عواقب فاجعه اتفاق می‌افتد. در‌حالی‌که همکاری بخش دولتی و خصوصی، یک همکاری بلندمدت و در طول زمان است. 
دیلمان و همکاران (2021) با استفاده از نظریه بازی به‌طور رسمی اثرات و وابستگی‌های تصمیم‌گیرندگان استراتژیک را توصیف کردند. این نظریه می‌تواند در تحلیل همکاری‌های بخش اضطراری به کار گرفته شود. همکاری‌های بخش اضطراری، دارای پتانسیل‌ها و محدودیت‌های خود هستند. به‌عنوان مثال، ناگورنی و همکاران (2016) در بررسی رقابت میان سازمان‌های بشردوستانه، از مدل تئوری بازی استفاده کردند. این مدل نشان می‌دهد سازمان‌های بشردوستانه در حال رقابت هستند و هم‌زمان برای به‌اشتراک‌گذاری منابع و کاهش هزینه همکاری می‌کنند. 
 (هولگین وراس و همکاران (2013) بیان کردند اصول اقتصادی رفاه باید در مدل‌های لجستیک بشردوستانه پس از فاجعه گنجانده شود تا به حصول استراتژی‌های تحویل با بیشترین منفعت برای بیشترین تعداد مردم منجر شود. تحلیل‌های مقاله استفاده از هزینه‌های اجتماعی (مجموع هزینه‌های لجستیک و محرومیت) را به‌عنوان تابع هدف ترجیحی برای مدل‌های لجستیک بشردوستانه پس از فاجعه پیشنهاد می‌کند.
 عبیدی و همکاران (2014) به خلأهای موجود در ارزیابی عملکرد در زنجیره تأمین بشردوستانه در مقابل تجربه‌های برگرفته از زنجیره تأمین تجاری پرداختند. در این مطالعه، دستورالعمل و راهنمایی برای چگونگی ارزیابی عملکرد در این فضا ارائه شده است که شامل معیارهای مربوط به ورودی و خروجی‌ها بود. طراحی زنجیره تأمین کمک‌رسانی و اهمیت و چگونگی بررسی عملکرد آن توسط هنگ و همکاران (2015) مورد بررسی قرار گرفت که در آن چارچوبی برای طراحی این زنجیره با در نظر گرفتن هزینه کلی لجستیک، سطح ریسک و میزان تقاضا پیشنهاد شده و رابطه بین این سه معیار عملکرد بررسی شد. حبیب و همکاران (2016) چالش عدم قطعیت در زمان، مکان و شدت فاجعه و شرایط بد زیرساخت‌های موجود را در مدیریت زنجیره تأمین بشردوستانه مورد مطالعه قرار دادند. در این مقاله، به جمع‌بندی و مرور مدل‌های ریاضی که در طی دهه پیش از زمان انتشار پژوهش ارائه شده بود پرداخته شد و ظرفیت‌های تحقیقاتی برای آینده شناسایی و و توضیح داده شد. 
وین و همکاران (2018) نقش و ظرفیت‌های همکاری اضطراری بین بخش عمومی و خصوصی در هنگام وقوع مخاطرات طبیعی را بررسی کردند. بر‌اساس این مدل ارائه‌شده، شانس بهبود عملیات مدیریت بحران با به‌اشتراک‌گذاری اطلاعات و تخصیص هماهنگ منابع و ظرفیت‌ها برای هر دو مرحله تشدید و کاهش تشدید یک فاجعه مشخص می‌شود. لی و همکاران (2018) به بررسی و مطالعه ساختار کلی در لجستیک زنجیره امداد بشردوستانه پرداختند و یک مدل پوشش همکاری بیشینه با ملاحظات بودجه برای به حداکثر رساندن منافع برای جمعیت آسیب‌دیده در مناطق فاجعه‌بار ارائه دادند. فتحعلیخانی و همکاران (2020) به بررسی تأثیر دخالت دولت در رویکردهای همکاری و رقابت در زنجیره تأمین بشردوستانه پرداختند و مدلی بر‌اساس نظریه بازی در این مورد ارائه دادند. 
ونکمولر و رینر (2020)، تحقیقات انجام‌شده در سال‌های اخیر را با تمرکز بر هماهنگی، همکاری و همکاری کوتاه‌مدت در‌زمینه مدیریت زنجیره تأمین امدادرسانی به‌منظور ارائه تعاریف منحصربه‌فرد از مفاهیم با در نظر گرفتن شرایط فاجعه بررسی کردند. در این تحقیق، مروری بر 202 مقاله دانشگاهی منتشرشده از سال 1996 به بعد در مجلات برتر مرتبط با هماهنگی، همکاری و همراهی زنجیره تأمین تدارکات و امداد تجاری انجام شد. باتوجه‌به رشد بلایا و اثرات مخرب آن‌ها در طول تاریخ، ضرورت مدیریت شایسته در زنجیره تأمین بشردوستانه پیش‌از‌پیش احساس می‌شود. همکاری بخش‌های دولتی و خصوصی در موفقیت کمک‌رسانی نقش مهمی دارد. دولت با استفاده از سناریوهای مختلف می‌تواند بر روی مزایای عضویت در این شرکت‌ها تأثیر بگذارد. در‌مورد زنجیره تأمین محصول، دولت می‌تواند با مداخله مناسب، به دستیابی به اهداف اجتماعی، مالی و زیست‌محیطی کمک کند (فتحعلیخانی و همکاران، 2020). 
حسینی مطلق و همکاران (2022) به‌طور خاص، یک مدل مبتنی بر نظریه بازی تکاملی، تحت عنوان «مکانیسم توزیع مازاد سود برای هماهنگی زنجیره تأمین» را پیشنهاد کردند تا بررسی کنند چگونه رفتارهای بلندمدت اعضای زنجیره تأمین بر تصمیم‌گیری اعضا برای هماهنگی و سهم آن‌ها از مازاد سود هماهنگی، تأثیر می‌گذارد. 
ارگون و همکاران (2023) یک مدل نظریه بازی برای برنامه‌ریزی لجستیک اضطراری ارائه دادند. برای انجام این کار، یک مدل بازی مشارکتی بر‌اساس یک مسئله که پس از زلزله در استانبول رخ داده است، ساخته شد و راه‌حل‌ها برای بیشینه‌سازی تعداد کالاهای کمک‌رسانی ارائه شده است. اریکان و همکاران (‌2023) مدلی 2 مرحله‌ای بر‌اساس اطلاعات فروشنده را در چارچوب یک بازی رهبر ـ پیرو بین یک سازمان بشردوستانه به‌عنوان رهبر و اهداکنندگان (پیرو) برای توصیف تعاملات آن‌ها ارائه دادند. در این مدل، سازمان بشردوستانه در‌مورد سطح پیش‌فرض برای آمادگی در برابر بلایا تصمیم‌گیری می‌کند. عدم قطعیت نیز در حین جمع‌آوری کمک‌های مالی در مرحله واکنش به بلایا تعیین می‌شود.
 لی و همکاران (2024) یک مدل بهینه‌سازی 2 سطحی برای تخصیص منابع در واکنش به بلایا، با تمرکز بر رابطه بین پرسنل و مواد ارائه کردند. این مدل از یک سطح بالایی تشکیل شده است که زمان نجات را از‌طریق برنامه‌ریزی حمل‌‍و‌‌نقل از شهرهای کمک‌کننده به مناطق آسیب‌دیده به حداقل می‌رساند و یک سطح پایین‌تر که هزینه‌های تخصیص منابع اضطراری از شهرهای کمک‌کننده به مراکز توزیع را به حداقل می‌رساند. هدف این مدل افزایش بازیابی پس از فاجعه، بهبود پایداری زنجیره تأمین و کاهش اثرات زیست‌محیطی است.
 کاتسالیاکی و همکاران (2024) تحقیقی شامل، مرور ادبیات سیستماتیک از 156 مقاله منتشر‌شده از سال 1997 الی 2022 در زنجیره تأمین رقابتی ـ همکاری انجام دادند، که در آن تئوری رقابت و روابط سازمانی را درون بنگاه‌ها و بین آن‌ها بررسی کردند. زنجیره‌های تأمین متمرکز بر همکاری بین تولیدکنندگان رقیب برای استفاده از قابلیت‌ها و عملکردهای زنجیره تأمین است. این تحقیق بر‌اساس مفهوم هم‌افزایی و نقش مدل مرجع عملیات زنجیره تأمین تدوین شده است. 
کسکن و همکاران (2024) از مدل‌های کمی مبتنی بر اطلاعات فروش برای بهینه‌سازی تصمیمات موجودی پیش از فاجعه تحت مکانیسم‌های همکاری متمرکز و غیرمتمرکز استفاده کردند. این مطالعه سطوح موجودی بهینه و تعادل نش را در هر دو سیستم شناسایی می‌کند و یک برنامه تصادفی 2 مرحله‌ای را با در نظر گرفتن عوامل قابلیت اطمینان تصادفی فرموله می‌کند. این مقاله با بینش‌های مدیریتی به پایان می‌رسد و تأکید می‌کند همکاری متمرکز زمانی ارجحیت دارد که تقاضا زیاد باشد. 
راموس و همکاران (2024) یک مدل تئوری بازی برای طراحی مبادلات منابع در پارک‌های اکو صنعتی ارائه دادند که بر‌اساس آن هر‌یک از مقامات یک پارک صنعتی را به‌عنوان یک بازیکن مستقل در نظر گرفت و بنابراین یک مدل بازی چند رهبر ـ چند پیرو ایجاد شد. شبکه‌های آب و انرژی به‌طور هم‌زمان در مدل از‌طریق یک مطالعه موردی شناخته‌شده ایجاد می‌شوند. مدل 2 سطحی نیز با در نظر گرفتن مدیران آب و انرژی به‌عنوان رهبر و کارخانه‌ها به‌عنوان پیرو طراحی شده است. ادسانور و همکاران (2023) تحلیلی از رویکردهای تحقیقات عملیاتی ارائه دادند که بر‌اساس تصمیم‌گیری بر‌اساس 3‌C بهبود‌یافته در زنجیره‌های امداد بشردوستانه بوده و خلأ تحقیقاتی آینده را شناسایی می‌کند. برای دستیابی به این هدف، ابتدا دیدگاهی جامع از مباحث موجود در ادبیات موردنظر بیان شد و یک چارچوب مفهومی بر‌اساس مکانیسم 3‌C در عملیات‌های بشردوستانه استخراج شده است.
پس از بررسی جامع مرور ادبیات یکی از خلأهای اساسی در فضای تحقیقاتی، وجود مدلی است که همکاری هم‌زمان دولت، سازمان‌های بشردوستانه بین‌المللی و داخلی را در کنار بخش خصوصی در نظر گرفته باشد. در‌نتیجه هدف از انجام این پژوهش، ارائه مدلی بر‌اساس نظریه بازی است که همکاری اهداکنندگان، سازمان‌های بشردوستانه، دولت و سازمان‌های بخش خصوصی را بررسی کند. در همین راستا و با هدف اطمینان حاصل کردن از ارائه پوشش حداکثری به نقاط آسیب‌دیده، مدلی ارائه می‌‌شود که با‌توجه‌به تعداد و تنوع بازیکنان، کمک‌رسانی باتوجه‌به ابعاد فاجعه و تعداد نقاط آسیب‌زده را بهینه می‌کند. همچنین با‌توجه‌به اینکه سازمان‌های بخش خصوصی هر‌کدام دارای ظرفیت‌ها (برای مثال فضای انبار و تعداد کالای کمکی)، سرعت عمل و کیفیت عملکردی متفاوتی هستند، در صورت تمایل به استفاده از کمک آنان در زمان فاجعه، می‌توان با انجام بررسی‌های کیفیتی در دوران پیشا‌فاجعه، سازمان‌های خصوصی واجد شرایط را در یک فهرست اضطراری لیست و بر‌اساس ظرفیت‌های لجستیکی طبقه‌بندی کرد. مدل موجود در این تحقیق، کیفیت خدمات و شایستگی سازمان‌های خصوصی را مد نظر قرار می‌دهد. این بخش این امکان را خواهد داد که در هنگام وقوع فاجعه، ترتیب پیش‌فرضی برای اولویت دادن به سازمان‌های خصوصی واجد شرایط دارای ظرفیت‌های مورد‌نیاز وجود داشته باشد. 

روش
در این قسمت یک مدل همکارانه زنجیره تأمین بشردوستانه ارائه می‌شود که به دنبال حداکثر‌سازی پوشش به نقاط آسیب‌دیده از‌طریق توزیع متناسب کالاهای 4 بازیکن اصلی و استفاده از ظرفیت کلی هر‌کدام است. زنجیره‌های تأمین بشردوستانه نوعی از زنجیره‌های تأمین هستند که هدف آن‌ها حداکثر کردن خدمت‌رسانی است؛ یعنی به مثابه زنجیره‌های تأمین کلاسیک هدف، زنجیره‌های تأمین بشردوستانه صرفاً صرفه جویی اقتصادی و حداکثرسازی سود نیستند. در این نوع زنجیره‌های تأمین، افراد آسیب‌دیده‌ای از مخاطرات طبیعی یا هر بحران دیگر وجود دارند که می‌بایست به‌موقع به آن‌ها خدمت‌رسانی شود. عدم خدمت‌رسانی به‌موقع به آن‌ها می‌تواند منجر به آسیب‌دیدگی‌های جدی‌تر یا حتی فوت آن‌ها شود. بنابراین یک زنجیره تأمین بشردوستانه باید به‌گونه‌ای طراحی شود که حتی اگر به دنبال حداقل کردن هزینه است اهداف دیگری، همچون اطمینان از تحویل کالاهای امدادی به حداکثر آسیب‌دیدگان به‌عنوان هدف دیگر در نظر گرفته شود. عموماً خدمت‌رسانی در شرایط بحران صرفاً از عهده یک نهاد خارج است و در کنار نهادهای دولتی که وظیفه اصلی و طبیعی مدیریت بحران و خدمت‌رسانی را برعهده دارند سازمان‌های بشردوستانه نیز وجود دارند که امکان خدمت‌رسانی دارند. سازمان‌های خیریه مردم‌نهاد که در نقاط مختلف و با حمایت مردم فعالیت دارند، دارای ظرفیت برای همکاری در کمک‌رسانی هستند. 
ازطرف‌دیگر، سازمان‌های کمک‌رسانی بین‌المللی متعددی در کشور حضور دارند که دارای بودجه و ظرفیت‌های کمک بلاعوض به کشور بوده و عمدتاً از دانش تخصصی لازم برای همکاری مؤثر و متقابل برخوردار هستند. از طرف دیگر این سازمان‌ها پل ارتباطی با حامیان مالی بین‌المللی بوده و امکان اخذ اقدام اضطراری برای به‌کارگیری بودجه موجود خود و یا افزایش آن جهت شرکت در عملیات کمک‌رسانی را دارند. بازیکن دیگری که ظرفیت‌های فراوانی داشته، اما کمتر در شرایط اضطراری به نظر می‌آید، بخش خصوصی است که باتوجه‌به کالاهای در دسترس و مراکز توزیع متعدد در سراسر کشور می‌تواند نقش تسهیل‌کننده و تسریع‌کننده قابل‌توجهی در کمک‌رسانی داشته باشند. گرچه این ظرفیت‌ها توسط این بازیکنان همواره موجود بوده است، نحوه ایجاد همکاری بین این نهادها به‌صورت هماهنگ به اندازه کافی بررسی نشده است که متأسفانه منجر به جلوگیری از چند باره شدن کمک‌رسانی به یک نقطه و از طرف دیگر بی‌نصیب ماندن نقطه‌ای دیگر در عملیات کمک‌رسانی می‌شود. 
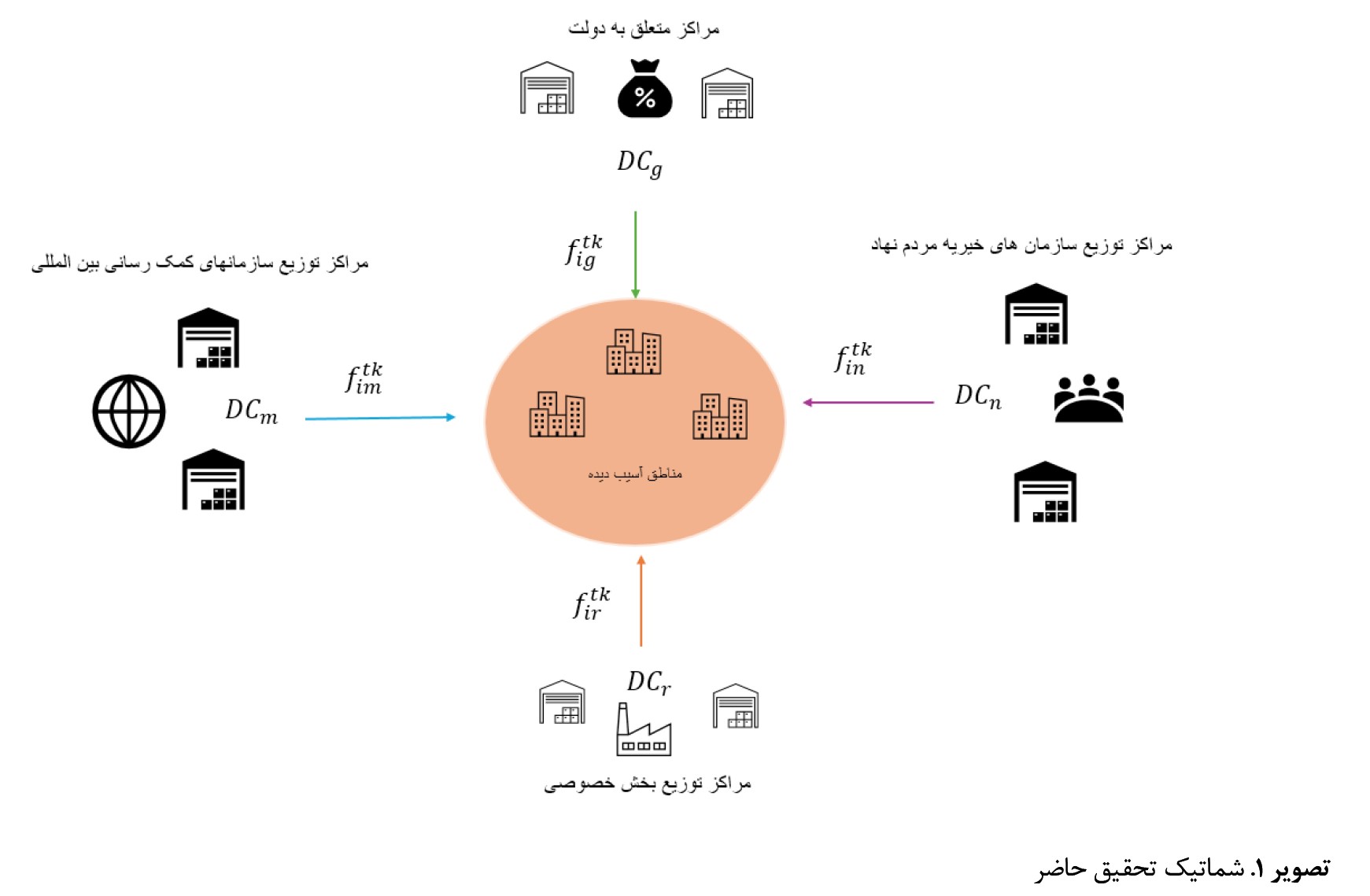
ازسوی‌دیگر فاصله بین نهادهای دولتی و مناطق آسیب‌دیده می‌تواند به حدی باشد که خدمت‌رسانی را به تعویق اندازد در‌حالی‌که سازمان‌های بشردوستانه به دلیل ازدیاد و همچنین همجواری بیشتر با مناطق آسیب‌دیده قادر به خدمت‌رسانی سریع‌تری هستند. بنابراین در تحقیق حاضر یک مدل همکاری بین دولت و نهادهای کمک‌رسانی مردم‌نهاد، سازمان‌های بشردوستانه بین‌المللی و همچنین بخش خصوصی در مدیریت بحران شکل می‌گیرد. به این ترتیب همکاری بین نهادها به وجود می‌آید. بر‌این‌اساس که کدام نهاد قادر به خدمت‌رسانی سریع‌تر ضمن بهره گیری بهینه از کالاهای موجود خواهد بود. در مدل حاضر، 4 بازیکن شامل دولت، سازمان‌های بشردوستانه بین‌المللی، سازمان‌های مردم‌نهاد و بخش خصوصی بوده و با هدف بیشینه‌سازی خدمات‌رسانی به نقاط آسیب‌دیده با یکدیگر همکاری می‌کنند. مدل ارائه‌شده در تحقیق حاضر با الهام از شکاف تحقیقاتی مرور ادبیات و مدل لی و همکاران، (2018) تدوین شده است. در تصویر شماره 1 شمای کلی زنجیره تأمین مورد‌نظر ارائه شده است.

مفروضات مدل
مفروضات مدل پیش‌رو به شرح ذیل است:
4 بازیکن در زنجیره تأمین وجود دارد: دولت، بخش خصوصی، سازمان‌های کمک‌رسانی بین‌المللی و سازمان‌های خیریه مردم‌نهاد.
هریک از بازیکنان بخش خصوصی بررسی‌های کیفیت قبل از فاجعه را پشت سر گذاشته‌اند.
یک لیست اضطراری بر‌اساس ساختارهای لجستیکی وجود دارد که نشان‌دهنده اولویت بازیکنان بخش خصوصی است و ضرایب صلاحیت هر بازیکن مشخص است.
هر بازیکن از‌نظر منابع، ظرفیت‌های متفاوتی دارد و منابع انواع کمک‌ها، مانند پتو، بسته‌های بهداشتی، چادر و غیره را شامل می‌شود.
سازمان‌های کمک‌رسانی بین‌المللی تنها در صورتی در عملیات کمک‌رسانی وارد می‌شوند که دولت به‌صورت واضح از آنان درخواست کند. در این مسئله شدت و ابعاد فاجعه به حدی است که دولت، کمک سازمان‌های بین‌المللی را درخواست کرده باشد که این شرط قانونی برای اقدام این سازمان‌هاست.
فاجعه اتفاق‌افتاده از نوع زلزله است و برخلاف فجایعی، ازجمله سیل و یا طوفان، امکان پیش‌بینی مسیر آن و انجام تخلیه شهروندان وجود نداشته است. 
کمک‌های تمامی‌حمایت‌کنندگان مالی اعم از غیر‌نقدی و منابع نقدی، به سازمان‌های کمک‌رسانی بین‌المللی اعطا می‌شود.
اطلاعات مسئله در بازه زمانی بلندمدت، ثابت است و نوع این مسئله ایستا است.
همه تصمیم‌گیرندگان (بازیکنان) از اهداف، محدودیت‌ها و اقدامات یکدیگر آگاهی کامل دارند.
بازیکنان منطقی عمل می‌کنند تا میزان پوشش نقاط آسیب‌دیده را به حداکثر برسانند.
ثبات تضمین می‌کند هیچ بازیکنی انگیزه‌ای برای جدا شدن نداشته باشد.
محدودیت‌های بودجه برای دولت تخصیص منابع را محدود می‌کند.
محدودیت‌های ظرفیت برای هر بازیکن (i) امکان‌پذیری همکاری را تضمین می‌کند.
هدف کلی ارائه حداکثر پوشش به مناطق آسیب‌دیده است.
همکاری مستلزم تخصیص کارآمد منابع است.
تقاضای هر نقطه آسیب‌دیده بلافاصله پس از فاجعه مشخص است و همه بازیکنان از آن مطلع هستند.

اندیس‌های مدل
i ∈ I: نشان‌دهنده منطقه آسیب‌دیده
g ∈ G: نشان‌دهنده مرکز توزیع متعلق به دولت
r ∈ R: نشان‌دهنده مرکز توزیع متعلق به بخش خصوصی
m ∈ M: نشان‌دهنده مرکز توزیع متعلق به سازمان کمک‌رسانی بین‌المللی
n ∈ N: نشان‌دهنده مرکز توزیع متعلق به مراکز خیریه مردم‌نهاد
k ∈ K: نشان‌دهنده نوع کالای کمکی
t ∈ T: نشان‌دهنده سناریوی احتمالی

مجموعه‌های مدل
{i1, i2, i3…, I} I =‌مجموعه نقاط آسیب‌دیده
 G =‌{g1, g2, g3, …gG}‌مجموعه مراکز توزیع متعلق به دولت
R= {r1, r2, r3…, rR}    مجموعه مراکز توزیع متعلق به بازیکنان بخش خصوصی
‌ {m1, m2, m3…, mM}M =مجموعه مراکز توزیع متعلق به سازمان کمک‌رسانی بین‌المللی
K= {k1, k2, k3…, kK} مجموعه اقلام، هر‌یک نشان‌دهنده یک کالای متفاوت
N= {n1, n2, n3…, nN} مجموعه مراکز توزیع متعلق به مراکز خیریه مردم‌نهاد
T= {t1, t2, t3…, tT}    مجموعه سناریوها

پارامترهای مدل 
dio : فاصله بین مرکز توزیع o و منطقه آسیب‌دیده Iو(o ∈ G ∪ R ∪ M ∪ N)
τ: حد پوشش
Fo‌: هزینه مکان‌یابی و ایجاد مرکز توزیع DCo برای دولت و یا به‌کارگیری مرکز توزیع متعلق به بازیکنان پیرو
ckio‌: هزینه واحد جابه‌جایی کالای نوع k از مرکز توزیع DCoو(o ∈ G ∪ R ∪ M ∪ N) به منطقه آسیب‌دیده 
hko: هزینه دریافت و ذخیره کالا در مراکز توزیع به ازای حجم
vk: حجم واحد کالای نوع k
Dtki : تقاضای مورد‌انتظار کالای نوع k در منطقه آسیب‌دیده i در سناریوی t
CAPo: ظرفیت مرکز توزیع DCoو(o ∈ G ∪ R ∪ M ∪ N)
Pt: احتمال تحقق سناریوی t    
ρk: ضریب اهمیت کالا k 0⩽ρ⩽1
B‌: بودجه پیش‌فرض    
γ r‌‌: ضریب صلاحیت / اثربخشی برای هر مرکز توزیع متعلق به بخش خصوصی که بر‌اساس ارزیابی پیشا‌فاجعه تعیین می‌شود، با شرط 0.2⩽γr⩽1
چنانچه برای یک مرکز توزیع بخش خصوصی γr <0.2 باشد، آن بنگاه بخش خصوصی در بررسی کیفی پیشا‌فاجعه رد شده است و در عملیات کمک‌رسانی شرکت نخواهد داشت.
Qko‌: تعداد کالای نوع k که در انبار (o ∈ G ∪ R ∪ M ∪ N) انبار می‌شوند.    

 متغیرهای مدل
f tkio: تقاضای اقلام نوع k در منطقه فاجعه‌زده i که توسط DCoو(o ∈ G ∪ R ∪ M ∪ N) در سناریوی t برآورده می‌شود. 
zr‌: برابر با 1 اگر از DCr متعلق به بخش خصوصی استفاده شود. در غیر این صورت  zr=0
zm‌‌: برابر با 1 اگر از DCm متعلق به سازمان کمک‌رسانی بین‌المللی استفاده شود. در غیر این صورت  zm=0
zn‌: برابر با 1 اگر از DCn متعلق به سازمان خیریه مردم‌نهاد استفاده شود. در غیر این صورت zn=0
xg‌: رابر با 1 اگر از DCg متعلق به دولت استفاده شود. در غیر این صورت zg=0
yi‌: برابر با 1 اگر منطقه فاجعه‌زده i در سناریوی t پوشش داده شود، در غیر این صورت ‌yi=0.    

ساختار ریاضی مدل
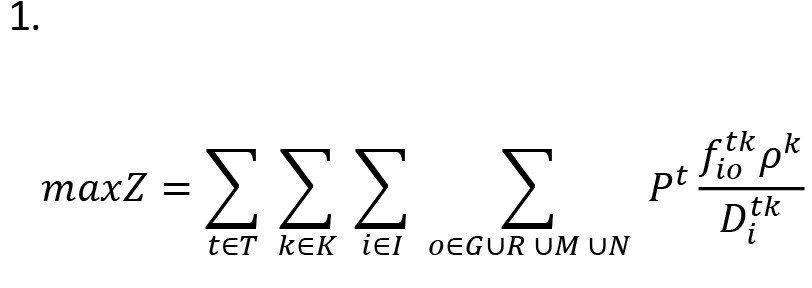
تابع هدف و محدودیت‌های مدل حاضر به شرح زیر است. (فرمول شماره 1):


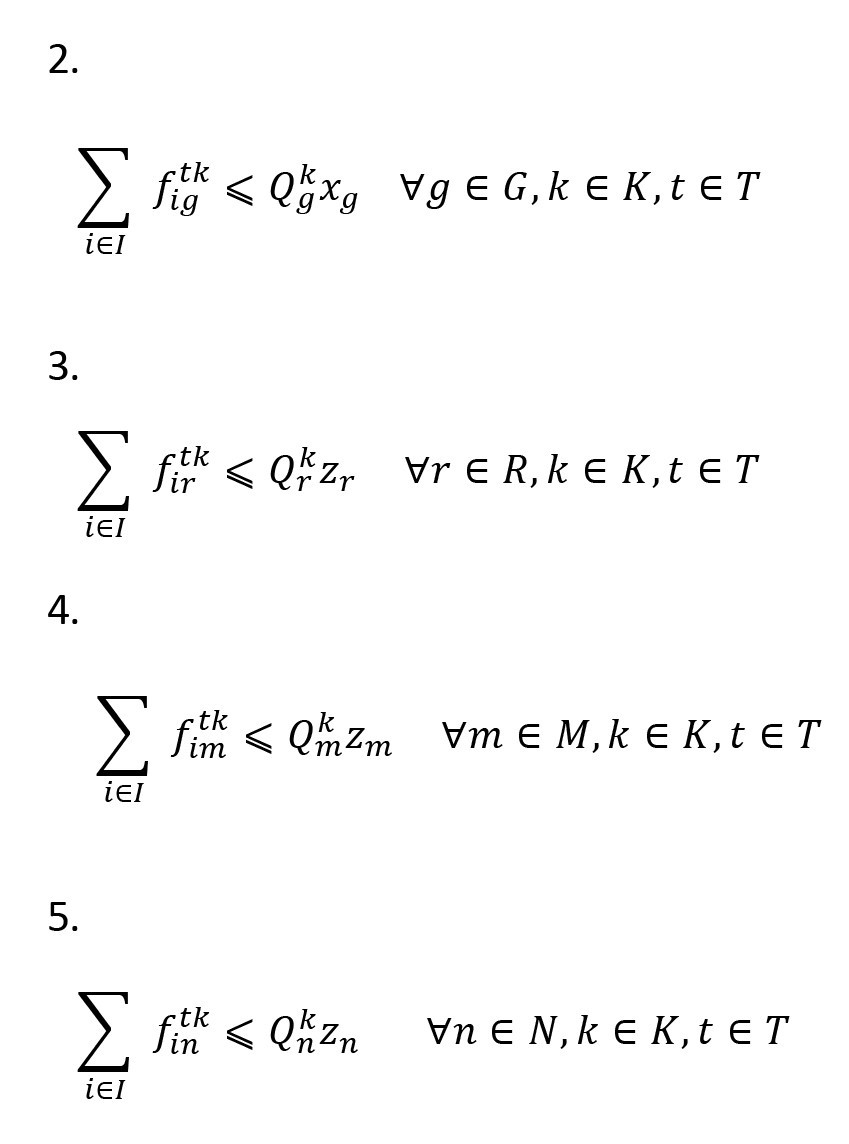
محدودیت‌های عرضه به شرح ذیل بوده و تضمین می‌کند موجودی در مراکز توزیع ایجاد‌شده یا به‌کارگیری‌شده می‌تواند مقدار تقاضای مناطق آسیب‌دیده را برآورده کند (فرمول‌های شماره 2، 3، 4، 5):


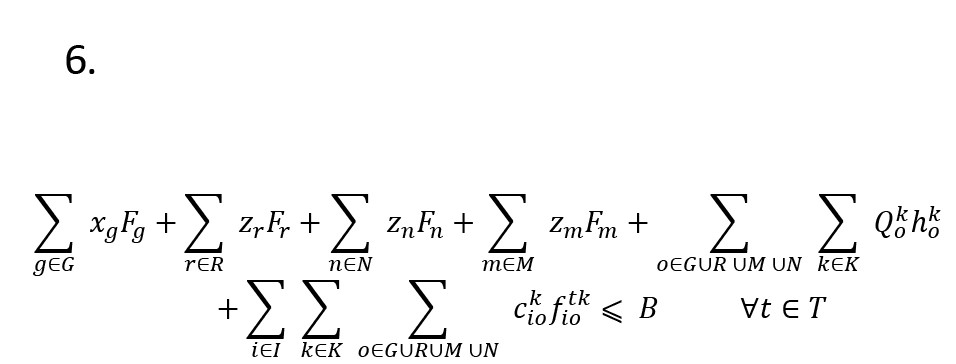
بر‌اساس محدودیت بودجه ذیل، هزینه ایجاد و استفاده از مراکز و هزینه ذخیره و ارسال اقلام امدادی از مراکز توزیع مستقر به مناطق فاجعه‌بار برای هر سناریو از بودجه پیش‌فرض بیشتر نخواهد شد (فرمول شماره 6). 


محدودیت ذیل یک آستانه پوشش را تعیین می‌کند که بر‌اساس آن هر مرکز توزیع تنها در صورتی نقطه آسیب‌زده را پوشش می‌دهد که مجموع سیگنال ساطع‌شده از مراکز توزیع بازیکنان مختلف از یک آستانه معین τ برای مناطق آسیب‌دیده فراتر رود. همچنین ضریب صلاحیت γr اطمینان حاصل می‌کند که امتیاز صلاحیت مراکز بخش خصوصی مدنظر قرار می‌گیرد و در ارزیابی، قدرت سیگنال آن در نظر گرفته می‌شود (فرمول شماره 7).


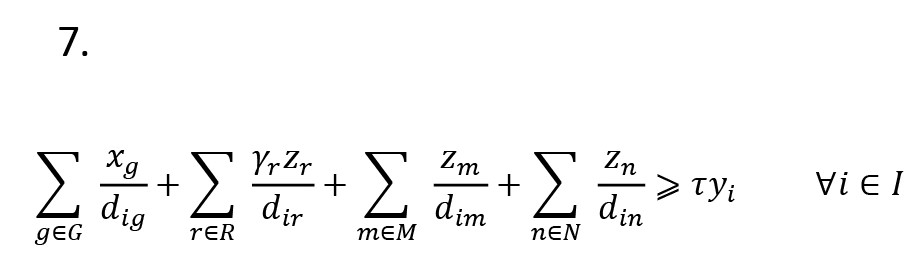
بر‌اساس 2 محدودیت تقاضا به شکل ذیل، مقادیر غیرمنفی اقلام امدادی ارسال‌شده برای برآورده کردن تقاضا در یک منطقه آسیب‌دیده نباید از تقاضای واقعی تجاوز کند و تنها در صورتی می‌توان آن‌ها را ارسال کرد که نیاز منطقه آسیب‌دیده را پوشش دهد (فرمول شماره 8 و 9).


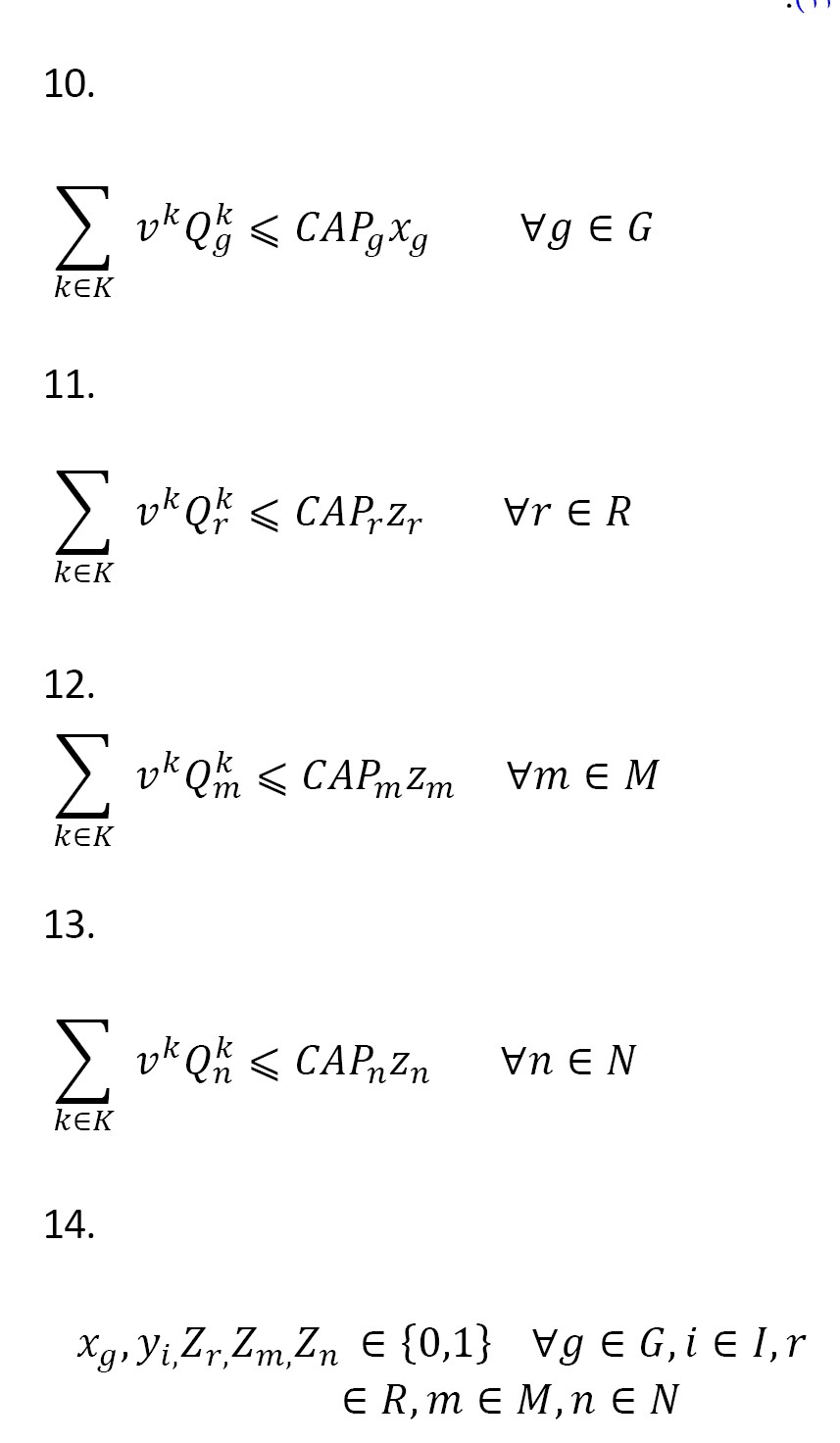
محدودیت‌های ذیل تضمین می‌کند اقلام صرفاً در مراکز توزیعِ مکان‌یابی‌شده و یا به کار گرفته‌شده و بر‌اساس ظرفیت حداکثری انبار مورد نظر ذخیره شوند (فرمول‌های شماره 10، 11، 12، 13، 14).



یافته‌ها
در این قسمت ابتدا یک مثال عددی با الهام از مسائل دنیای واقعی برای نشان دادن کاربرد مدل ارائه می‌شود. سپس مسئله مورد‌نظر با استفاده از نرم‌افزار گمز، فرموله شده و محدودیت‌ها و اهداف پیاده‌سازی می‌شوند. در‌نهایت آنالیز حساسیت روی چند پارامتراز مدل انجام خواهد شد. در جدول‌های 1، 2، 3، 4، 5، 6، 7، 8، 9، 10، 11، 12، 13، 14، 15، 16، 17 و 18 تمام مقادیر مورداستفاده برای پارامترهای موردنیاز اعم از هزینه و ... آورده شده است. 






















































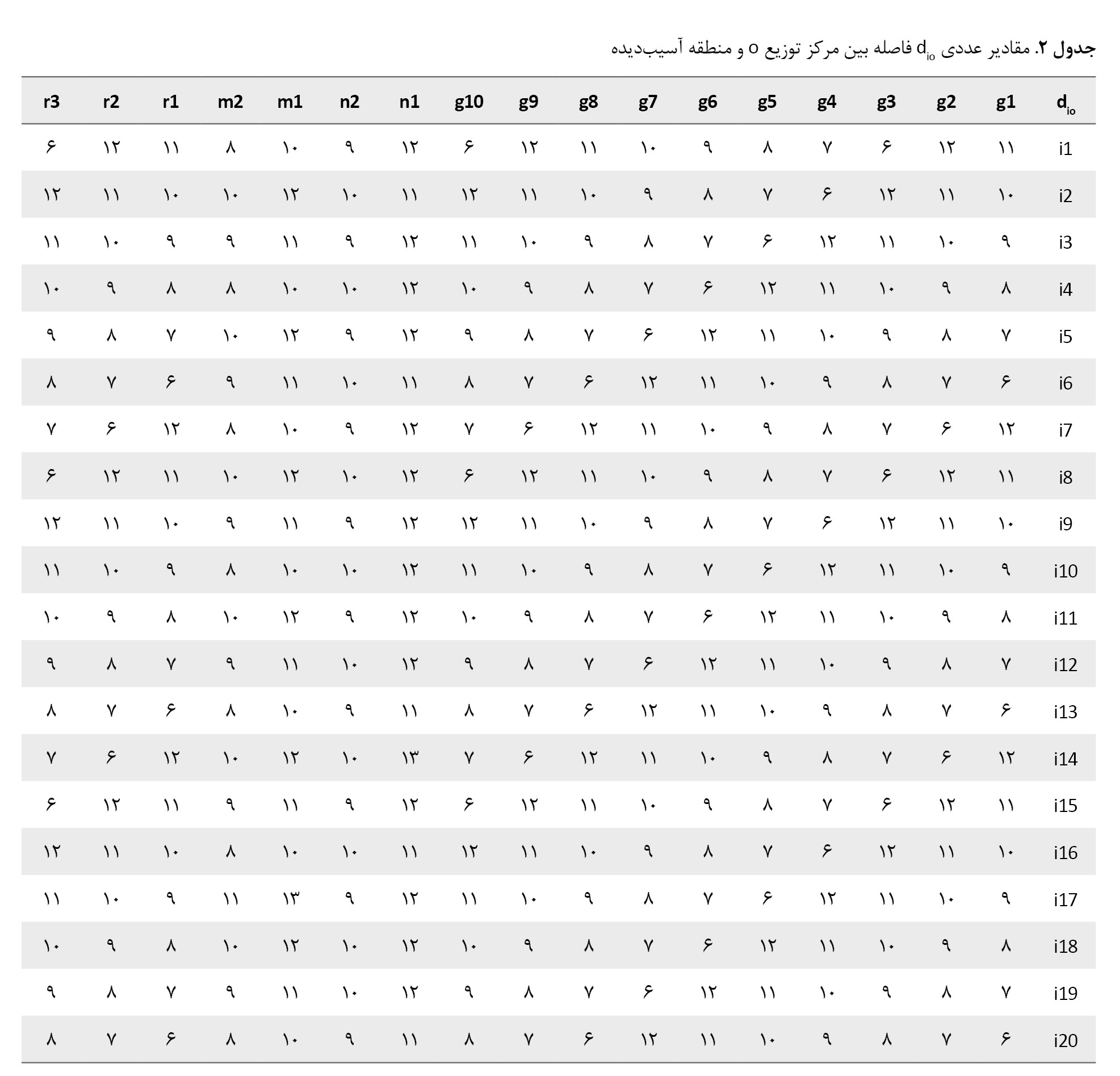
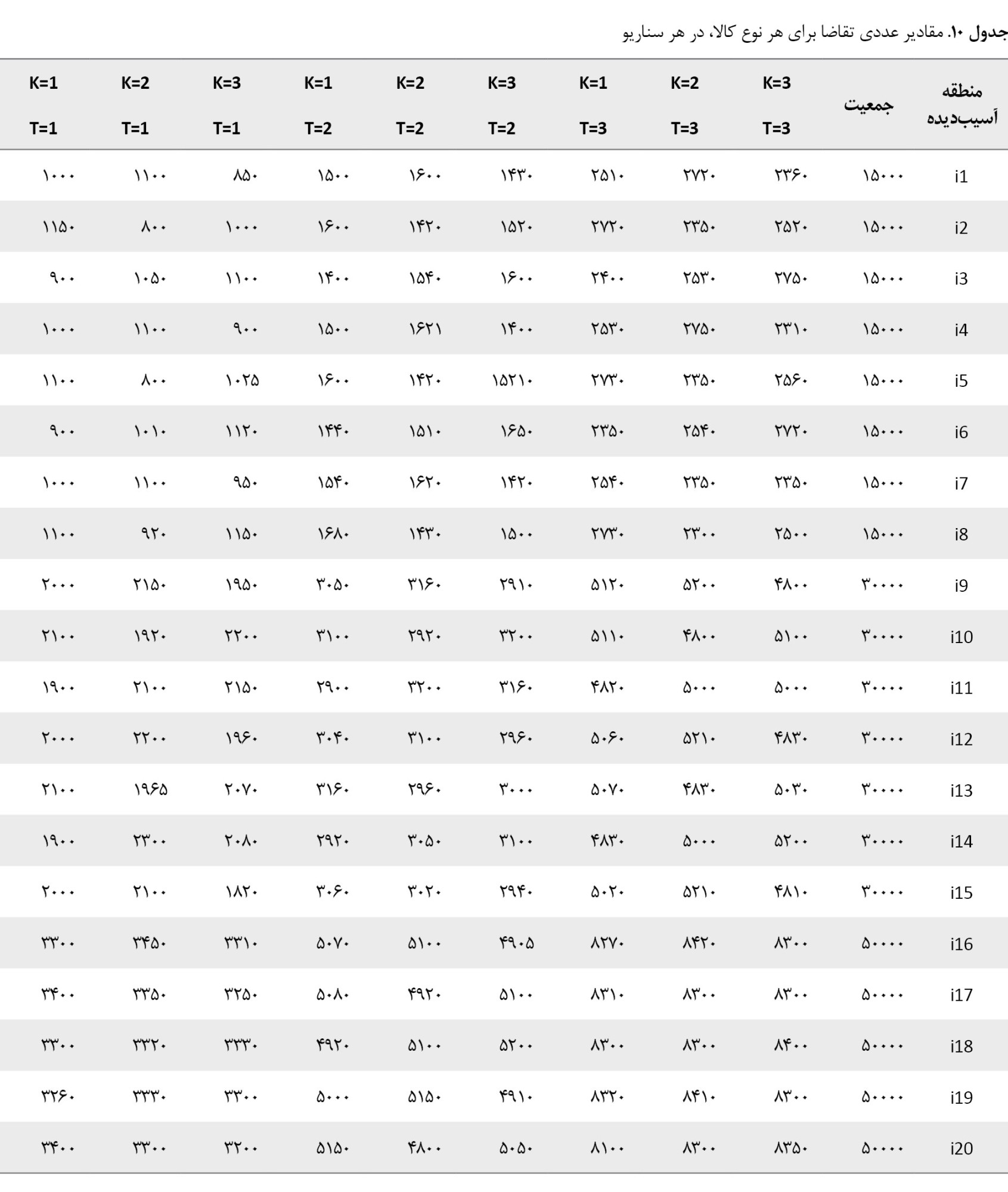
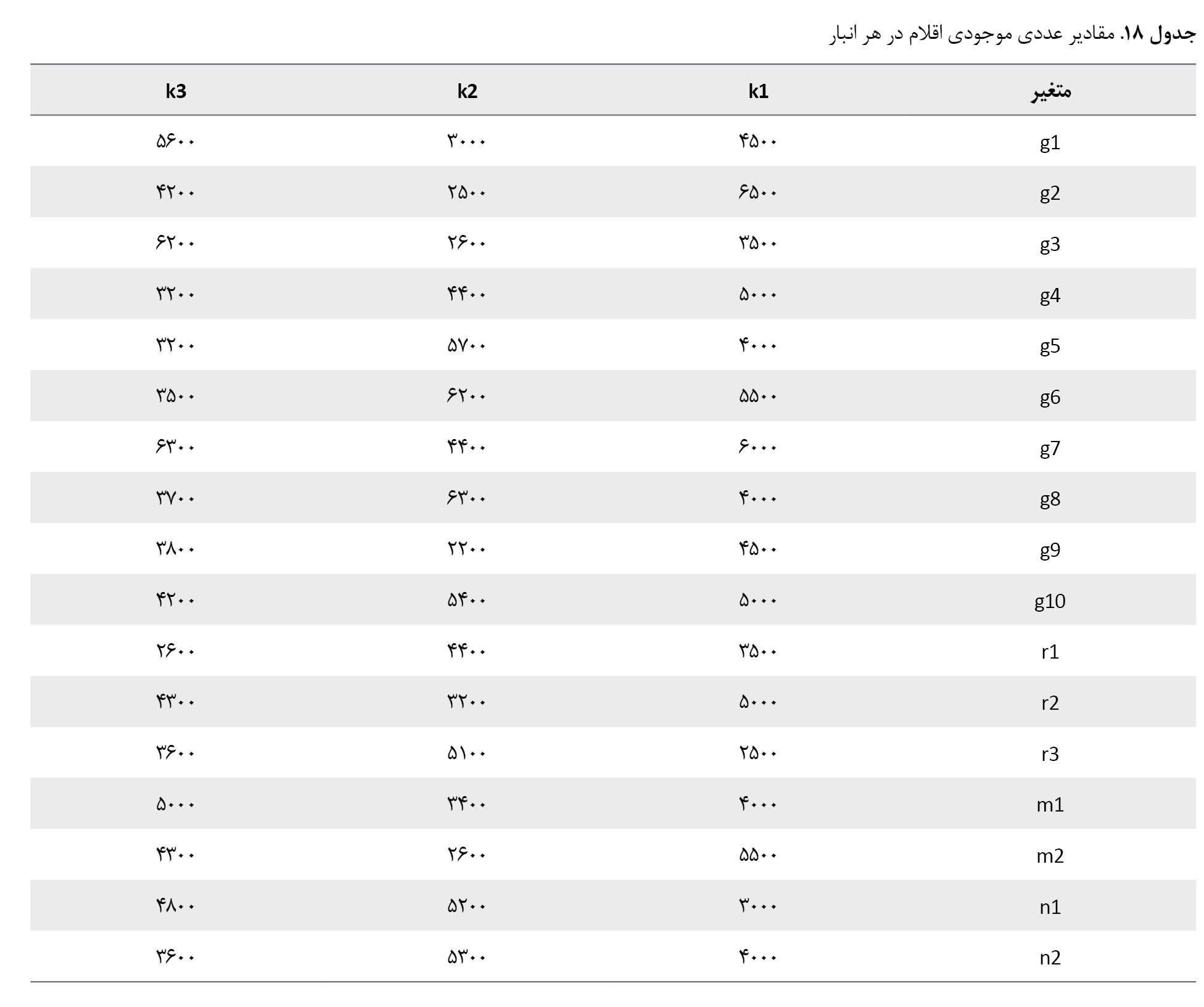
 مثال عددی
برای شبیه‌سازی مدل، مقادیر عددی به پارامترهای تعریف‌شده به شرح ذیل اطلاق می‌شود:

بودجه پیش فرض: 5000000000 واحد پولی
حد پوشش یا τ برابر 0/3 در نظر گرفته می‌شود.
3 سناریوی (تقاضای کم) t1 ،‌t2 (تقاضای متوسط) و t3 (تقاضای زیاد) در نظر گرفته شده است.
در جدول شماره 8، هزینه دریافت و ذخیره کالا برای مرکز متعلق به سازمان کمک‌رسانی بین‌المللی برابر صفر در نظر گرفته شده است، چرا‌که این سازمان‌ها به دلیل در اختیار داشتن بودجه، این بخش از هزینه را در قالب کمک پوشش می‌دهند؛ بنابراین بودجه کمک‌رسانی مصرف نمی‌شود.
در جدول شماره 10، مشاهده می‌شود در سناریو‌های مختلف، مقدار تقاضا کم، متوسط و زیاد در نظر گرفته شده است. میزان تقاضا نیز با‌توجه‌به عدد جمعیت هر منطقه آسیب‌دیده متفاوت بوده و با افزایش جمعیت بیشتر می‌شود.
مدل‌سازی مسئله در نرم‌افزار گمز نشان می‌دهد تقاضای موردنیاز هر نقطه آسیب‌دیده توسط انبارهای دارای کالای موردنظر فراهم شده است. تمامی انبارها نیز به کار گرفته شده و به نظر می‌رسد مقدار پارامتر حد پوشش بر شعاع توزیع کمک تأثیر مستقیم دارد. درصد پوشش در سناریو با کمترین تقاضا، بیشترین و درصد پوشش در سناریو با بیشترین پوشش، کمترین بوده است. بر‌اساس داده‌های جدول‌های شماره 10 و 18 جمع موجودی قابل‌عرضه توسط کلیه انبارها در هر سه سناریو یکی بوده و صرفاً مقدار تقاضا در هر سناریو افزایش می‌یابد. در سناریوی اول جمع تقاضای نقاط از جمع موجودی‌ها حدود 88 درصد کمتر بوده است و میزان تخصیص منابع تحت تأثیر حد پوشش و فاصله نقاط تا انبار میزان پوشش تعیین می‌شود. در سناریوی دوم جمع تقاضا بیشتر از سناریوی اول بوده و موجودی انبارها 16 درصد بیشتر از تقاضا است. در سناریوی سوم جمع تقاضا به میزان 30 درصد بیشتر از موجودی کلیه انبارها بوده است. 

آنالیز حساسیت
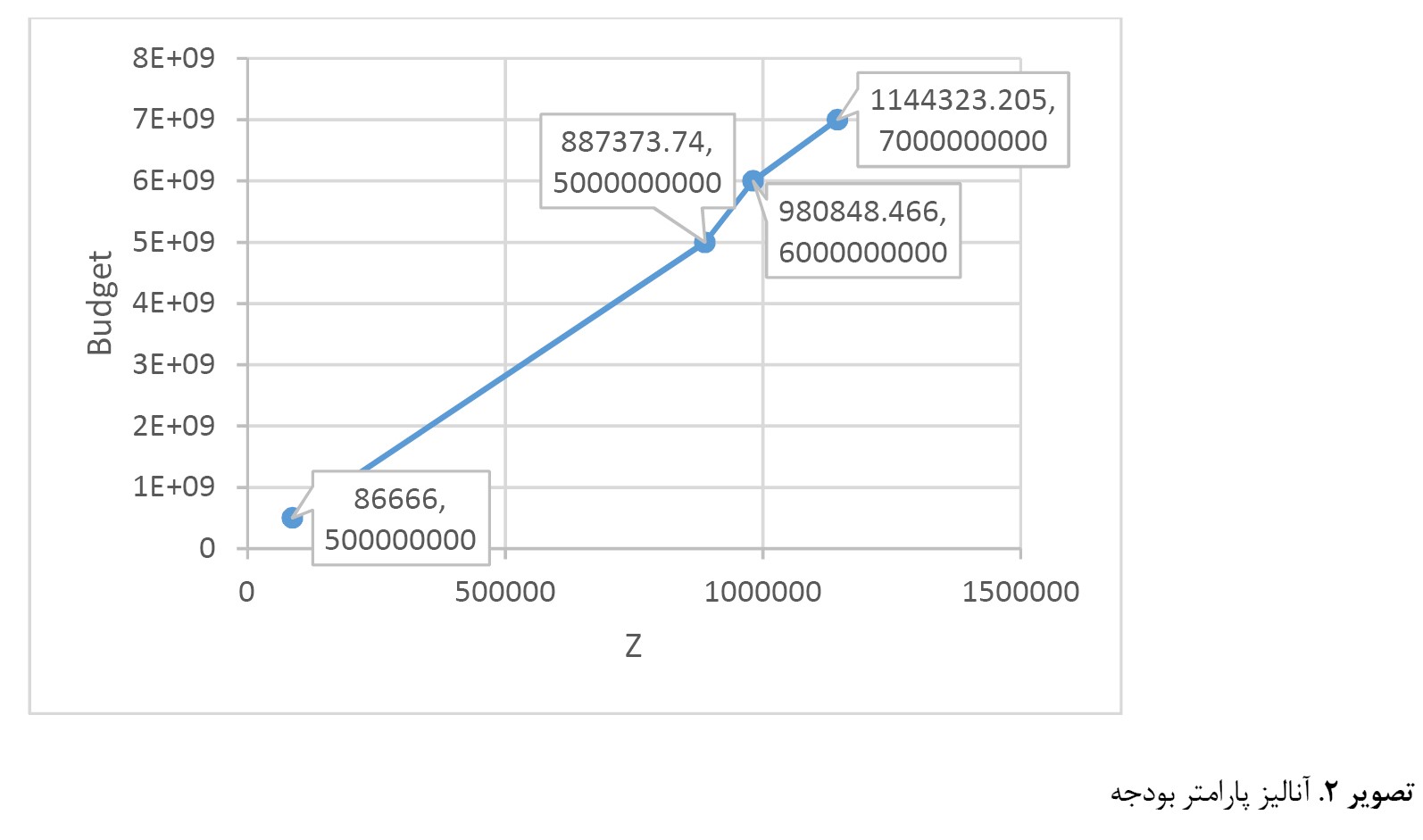
برای آنالیز حساسیت مدل، 5 پارامتر بررسی شده‌اند که شامل پارامتر بودجه کل عملیات و 4 پارامتر موجودی انبارهای هر بازیکن است. تصویر شماره 2 رابطه بودجه با مقدار تابع هدف را نشان می‌دهد که حاکی از رابطه‌ای نسبتاً خطی است.

تصویر شماره 3 نشان‌دهنده آنالیز حساسیت 4 پارامتر QKn ،QKm  ،QKr ،QKq است که به ترتیب معادل میزان کالاهای موجود در مراکز توزیع دولت، بخش خصوصی، سازمان‌های بشردوستانه و سازمان‌های خیریه مردم‌نهاد است.

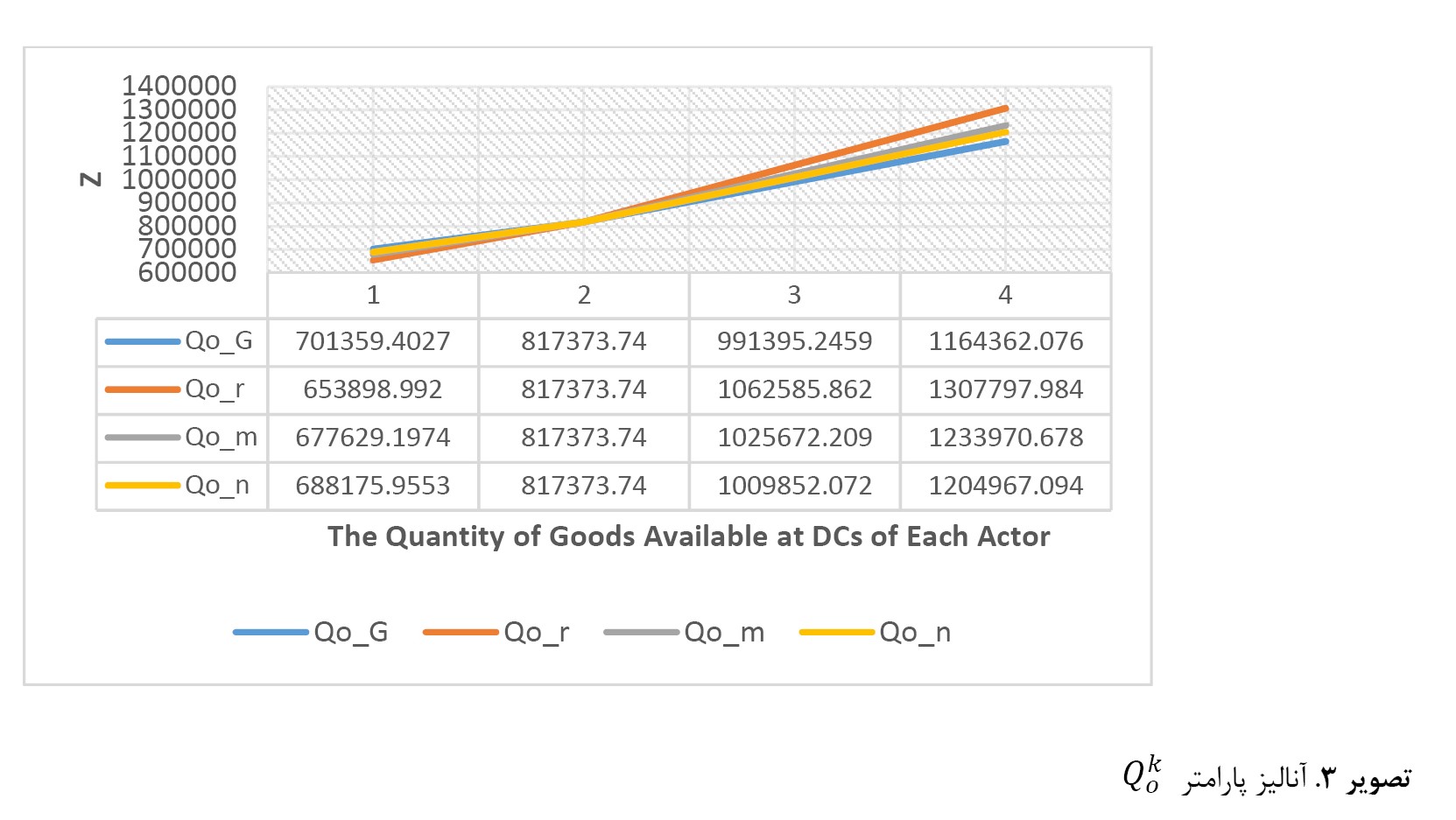
ستون‌های جدول موجود در تصویر شماره 3، نشان‌دهنده 4 حالت عدد‌دهی به پارامتر است. به‌ترتیب، ستون 1 نشان‌دهنده مقدار تابع هدف بهینه در صورت کاهش میزان کل موجودی مراکز توزیع هر بازیکن، به یک‌سوم مقدار مثال عددی، ستون 2 معادل مقادیر عددی مذکور، ستون سوم معادل 2 برابر مقادیر مثال عددی و ستون چهارم معادل 3 برابر مقادیر مثال عددی بوده است. بر‌اساس نتیجه این تحلیل، نمودار مربوط به دولت دارای کمترین شیب و نمودار مربوط به بخش خصوصی دارای بیشترین شیب است. این موضوع حاکی از این است که در صورت نیاز به افزایش موجودی بازیکنان برای افزایش پوشش و تقاضا، بهترین راه‌حل تخصیص کالای بیشتر به بازیکنان بخش خصوصی است. بعد از بخش خصوصی، به ترتیب سازمان‌های بشردوستانه بین‌المللی و پس از آن سازمان‌های مردم‌نهاد داخلی و در آخر دولت گزینه‌های بهینه برای افزایش مقدار بهینه تابع هدف و در‌نتیجه بیشینه‌سازی پوشش نقاط هستند.

بحث
در این پژوهش، مدلی همکارانه ارائه شد که به‌منظور پوشش حداکثری نقاط آسیب‌دیده ناشی از فاجعه‌های طبیعی طراحی شده است. بازیگران اصلی این مدل شامل دولت، بخش خصوصی، سازمان‌های بشردوستانه بین‌المللی و سازمان‌های غیر‌دولتی داخلی بودند. این مدل نوآورانه که مشابه آن در مطالعات دردسترس وجود نداشته، می‌تواند به‌عنوان یک چارچوب جدید برای ارتقای هم‌افزایی و هماهنگی میان این 4 بازیکن عمل کند و به بهبود پاسخگویی به چالش‌های اجتماعی و انسانی کمک کند. هر‌یک از این بازیگران دارای ظرفیت‌های متنوعی، از‌جمله مراکز توزیع متعدد و انواع مختلف کالاها هستند. مدل طراحی‌شده با استفاده از یک نمونه عددی فرضی و نرم‌افزار گمز حل شده و تحلیل حساسیت نیز انجام شده است. نتایج به‌دست‌آمده از مدل، بینش‌های ارزشمندی را در‌مورد اقدامات بهینه هر‌یک از بازیکنان در زنجیره تأمین در طول یک فاجعه ارائه می‌کند. این مدل ظرفیت‌ها و قابلیت‌های هر بازیکن و همچنین کیفیت خدمات ارائه‌شده توسط بخش خصوصی را در نظر می‌گیرد و امکان تخصیص کارآمدتر منابع را فراهم می‌کند و حداکثر پوشش نقاط آسیب‌دیده را تضمین می‌کند. این مدل همچنین بررسی‌های کیفی انجام‌شده در دوران پیش از فاجعه را در نظر می‌گیرد و می‌تواند به‌طور قابل‌توجهی اثربخشی تلاش‌های مدیریت بلایا را بهبود بخشد. نظر به اینکه پژوهش حاضر بر‌اساس داده‌های فرضی انجام شده است، پیشنهاد می‌شود در آینده مدل پیشنهادی در قالب یک مطالعه موردی بررسی شود. 

نتیجه‌گیری
با وجود اینکه مسئولیت اجتماعی اهمیت زیادی یافته است و در سال‌های اخیر این موضوع منتج به همکاری بدون چشمداشت شرکت‌های خصوصی در فجایع طبیعی و انسانی شده است، جهت افزایش آمادگی برای رسیدگی به عواقب یک فاجعه، پیشنهاد می‌شود طی یک آگهی دعوت به همکاری، از شرکت‌های خصوصی علاقه‌مند دعوت شود تا در ازای برخورداری از مزایایی از‌جمله بخشودگی مالیاتی از سمت دولت، آمادگی خود را جهت کمک در صورت وقوع فاجعه اعلام کنند. سازمان‌های کمک‌رسانی بین‌المللی به دلیل داشتن ظرفیت‌های مورد نیاز و با هدف کمک به دولت، می‌توانند ارزیابی فنی شرکت‌های داوطلب را انجام داده و فهرستی از شرکت‌های داوطلب و اولویت کیفی هریک را بررسی و آماده کنند. سازمان‌های بین‌المللی دارای فهرستی از فروشندگان سرویس و کالا هستند که در طول زمان با آن‌ها کار کرده‌اند. بنابراین چنانچه شرکت‌های خصوصی داوطلب در این لیست باشند، می‌‌توانند بر‌اساس ارزیابی‌های عملکردی پیشین خود که در آرشیو سازمان‌های بین‌المللی کمک‌رسانی قرار دارد به لیست داوطلبین اضافه شوند. جهت بررسی بهتر صلاحیت بنگاه‌های خصوصی، پیشنهاد می‌شود یک مدل برای محاسبه مطلوبیت و اولویت‌بندی شرکت‌های بخش خصوصی ارائه شود که ذر آن عوامل مختلف ازجمله شماره ابعاد یگان حمل، دامنه پوشش، تعداد انبارهای عادی و یخچالی موجود در سطح کشور وزن‌دهی شوند. این مدل می‌تواند جهت ارزیابی‌های دوره ای شرکت‌های داوطلب مورد بررسی قرار گیرد. عامل دیگری نیز وجود دارد که می‌تواند در یک مدل تئوری بازی مشارکتی برای زنجیره تأمین بشردوستانه گنجانده شود. برخی از این عوامل عبارت‌اند از:
- کیفیت و قابلیت اطمینان وسایل نقلیه ارائه‌شده توسط بخش خصوصی.
- کیفیت و قابلیت اطمینان کالاهای کمکی ارائه‌شده توسط سازمان‌های کمک‌رسان بین‌المللی و سازمان‌های غیردولتی و سازمان‌های کمک‌رسان ملی.
- توانایی دولت برای هماهنگ کردن تلاش‌های همه بازیکنان در زنجیره تأمین.
- توانایی دولت برای واکنش سریع به شرایط در حال تغییر.
- هنجارهای فرهنگی و اجتماعی منطقه آسیب‌دیده.
- در دسترس بودن منابع محلی، مانند نیروی کار، حمل‌و‌نقل و امکانات ذخیره‌سازی.
- تأثیر شرایط محیطی، مانند کیفیت جاده‌ها و آسیب وارده به آن‌ها بر اثر فاجعه، آب‌و‌هوا و فصول.

ملاحظات اخلاقی
پیروی از اصول اخلاق پژوهش
این مقاله نمونه های انسانی و حیوانی نداشته است. براین اساس نیاز به کد اخلاق نبوده و تمام قوانین اخلاق در پژوهش رعایت شده است.

حامی مالی
این مقاله برگرفته از رساله کارشناسی ارشد گلنوش جهرمی رجبی دانشگاه آزاد اسلامی، واحد تهران شمال می‌باشد و هیچگونه کمک مالی از سازمان های دولتی، خصوصی و غیرانتفاعی دریافت نکرده است.

مشارکت نویسندگان
اعتبارسنجی، تحلیل رسمی، تحقیق، منابع، جمع‌آوری داده‌ها: گلنوش جهرمی رجبی؛ مفهوم‌سازی و روش‌شناسی: راضیه کشاورزفرد و گلنوش جهرمی رجبی؛ نگارش پیش‌نویس اولیه، بررسی و ویرایش و نظارت: راضیه کشاورزفرد.

تعارض منافع
بنابر اظهار نویسندگان، این مقاله تعارض منافع ندارد.

References
Abidi, H., De Leeuw, S., & Klumpp, M. (2014). Humanitarian supply chain performance management: A systematic literature review. Supply Chain Management: An International Journal, 19(5/6), 592-608. [Link] 
Adsanver, B., Balcik, B., Bélanger, V., & Rancourt, M. E. (2023). Operations research approaches for improving coordination, cooperation, and collaboration in humanitarian relief chains: A framework and literature review. Quebec: CIRRELT. [Link]
Aldashev, G., & Verdier, T. (2010). Goodwill bazaar: NGO competition and giving to development. Journal of Development Economics, 91(1), 48-63. [DOI:10.1016/j.jdeveco.2008.11.010] 
Arikan, E., Silbermayr, L., & Toyasaki, F. (2023). Interplay between humanitarian procurement operations and fundraising. Computers & Industrial Engineering, 184, 109559. [DOI:10.1016/j.cie.2023.109559] 
Chen, J., Chen, T. H. Y., Vertinsky, I., Yumagulova, L., & Park, C. (2013). Public–private partnerships for the development of disaster resilient communities. Journal of Contingencies and Crisis Management, 21(3), 130-143. [Link]
Coles, J., & Zhuang, J. (2011). Decisions in disaster recovery operations: A game theoretic perspective on organization cooperation. Journal of Homeland Security and Emergency Management, 8(1), 1-16. [Link] 
Coskun, A., Salman, F. S., & Pashapour, A. (2024). Relief item inventory planning under centralized and decentralized bilateral cooperation and uncertain transshipment quantities. Socio-Economic Planning Sciences, 95, 101991. [DOI:10.1016/j.seps.2024.101991] 
Day, J. M., Melnyk, S. A., Larson, P. D., Davis, E. W., & Whybark, D. C. (2012). Humanitarian and disaster relief supply chains: A matter of life and death. Journal of Supply Chain Management, 48(2), 21-36. [Link] 
Diehlmann, F., Lüttenberg, M., Verdonck, L., Wiens, M., Zienau, A., & Schultmann, F. (2021). Public-private collaborations in emergency logistics: A framework based on logistical and game-theoretical concepts. Safety Science, 141, 105301. [DOI:10.1016/j.ssci.2021.105301] 
Ergün, S., Usta, P., Alparslan Gök, S. Z., & Weber, G. W. (2023). A game theoretical approach to emergency logistics planning in natural disasters. Annals of Operations Research, 324(1), 855-868. [Link] 
Fathalikhani, S., Hafezalkotob, A., & Soltani, R. (2018). Cooperation and coopetition among humanitarian organizations: A game theory approach. Kybernetes, 47(8), 1642-1663.[DOI:10.1108/K-10-2017-0369] 
Fathalikhani, S., Hafezalkotob, A., & Soltani, R. (2020). Government intervention on cooperation, competition, and coopetition of humanitarian supply chains. Socio-Economic Planning Sciences, 69, 100715. [DOI:10.1016/j.seps.2019.05.006] 
Habib, M. S., Lee, Y. H., & Memon, M. S. (2016). Mathematical models in humanitarian supply chain management: A systematic literature review. Mathematical Problems in Engineering, 2016(1), 3212095. [DOI:10.1155/2016/3212095] 
Holguín-Veras, J., Pérez, N., Jaller, M., Van Wassenhove, L. N., & Aros-Vera, F. (2013). On the appropriate objective function for post-disaster humanitarian logistics models. Journal of Operations Management, 31(5), 262-280. [DOI:10.1016/j.jom.2013.06.002] 
Hong, J. D., Jeong, K. Y., & Feng, K. (2015). Emergency relief supply chain design and trade-off analysis. Journal of Humanitarian Logistics and Supply Chain Management, 5(2), 162-187. [DOI:10.1108/JHLSCM-05-2014-0019] 
Hosseini-Motlagh, S. M., Choi, T. M., Johari, M., & Nouri-Harzvili, M. (2022). A profit surplus distribution mechanism for supply chain coordination: An evolutionary game-theoretic analysis. European Journal of Operational Research, 301(2), 561-575. [DOI:10.1016/j.ejor.2021.10.059] 
Katsaliaki, K., Kumar, S., & Loulos, V. (2024). Supply chain coopetition: A review of structures, mechanisms and dynamics. International Journal of Production Economics, 267, 109057. [DOI:10.1016/j.ijpe.2023.109057] 
Li, J., Zhang, X., & Yao, Y. (2024). A bi-level robust optimization model for the coupling allocation of post-disaster personnel and materials assistance. Journal of Cleaner Production, 469, 143099.  [DOI:10.1016/j.jclepro.2024.143099] 
Li, X., Ramshani, M., & Huang, Y. (2018). Cooperative maximal covering models for humanitarian relief chain management. Computers & Industrial Engineering, 119, 301-308. [DOI:10.1016/J.CIE.2018.04.004] 
Muggy, L., & Heier Stamm, J. L. (2014). Game theory applications in humanitarian operations: A review. Journal of Humanitarian Logistics and Supply Chain Management, 4(1), 4-23. [DOI:10.1108/JHLSCM-07-2013-0026] 
Nagurney, A., Flores, E. A., & Soylu, C. (2016). A Generalized Nash Equilibrium network model for post-disaster humanitarian relief. Transportation Research Part E: Logistics and Transportation Review, 95, 1-18. [DOI:10.1016/j.tre.2016.08.005] 
Ramos, M. A., Boix, M., Aussel, D., & Montastruc, L. (2024). Development of a multi-leader multi-follower game to design industrial symbioses. Computers & Chemical Engineering, 183, 108598. [DOI:10.1016/j.compchemeng.2024.108598] 
Schulz, S. F., & Blecken, A. (2010). Horizontal cooperation in disaster relief logistics: benefits and impediments. International Journal of Physical Distribution & Logistics Management, 40(8/9), 636-656. [DOI:10.1108/09600031011079300] 
Wankmüller, C., & Reiner, G. (2020). Coordination, cooperation and collaboration in relief supply chain management. Journal of Business Economics, 90, 239-276. [Link] 
Wiens, M., Schätter, F., Zobel, C.W., Schultmann, F. (2018). Collaborative emergency supply chains for essential goods and services. In A. Fekete & F. Fiedrich (Eds), Urban Disaster Resilience and Security. The Urban Book Series. Cham: Springer. [Link]
Zhuang, J., Saxton, G. D., & Wu, H. (2014). Publicity vs. impact in nonprofit disclosures and donor preferences: A sequential game with one nonprofit organization and N donors. Annals of Operations Research, 221(1), 469-491. [Link]